Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Степень и базис простого алгебраического расширения.Содержание книги
Поиск на нашем сайте
Опр: Пусть Опр: Опр: Опр: Т: Конечное расширение конечного расширения является конечным расширением.
Пусть [ [
Тогда мн-вом таких произведений
Док-во: 1) Докажем, что система
f=
f= 2) Докажем линейную независимость.
Но
7. Исключение ирр. в знаменателе(через векторные пространства) Если дано f(z)/g(z) и z алгебраическое над Р, р(z) наименьший полином степень которого равна n, то расширение P(z) над Q имеет размерность n и базисом является 1, z,z2,z3,……..,zn-1. Значит эта дробь единственным образом раглагается в виде а0, а1z,а2z2,а3z3,……..,аn-1zn-1, если минимальный многочлен эл-та z имеет степень n.Освободится от ирр. в знаменателе α/α-1 если а корень f(z)=x3+x-3. Базис 1, α, α2. α/α-1=А∙1+В∙α+С∙α2 α= (А∙1+В∙α+С∙α2)∙(α-1) α=А∙α+ В∙α2+ С∙α3-A –B∙α-C∙α2 выразим α3 через f(z). α3=3-α, подставим: α=α2∙ (B-C)+ α∙ (A-C-B)+3∙C – A составим систему уравнений из коофициентов при а и решим ее.
A-C-B=1 A=3C A=3 и подставим полученные коофициенты: α/α-1=3+ α+α2 3C-A=0 3C-C-C=1 C=1
Исключение ирр. в знаменателе(через минимальный многочлен) Пусть а – неприводимое иррациональное число. p(x) Подставим а. u(а)g(а)+v(а)p(а)=1
g(a)u(a)=1 => h(x)=f(x)u(x) h(x) – не содержит иррациональных знаменателей, следовательно, мы решили задачу. а/а-1=f(a)/g(a) p(x)= x3+x-3 найдем НОД(p(а) и g(a)). a3+а-3=(а-1) ∙ (а2+a+2)+1 x3+x-3=(x-1) ∙ (x2+x+2)+1 -1=(x-1) ∙ (x2+x+2)+(- x3-x+3), где последняя скобка = p(x)=0 т.к. имеет место алгебраическое равенство, то имеет равенство и функциональное -1=(а-1) ∙ (а2+а+2) значит (а/(а-1)) ∙ (а-1) ∙ (а2+а+2)= а3+а+2=3-а+ а2+2а=3+ а+а2
Конечно порождённые расширения. Определения и строение. Опр.5.1 Пусть заданы вложения полей Р с Т с F (1)’. Тогда (1) наз. цепочкой расширения. P=P1 c P2 c…c Pz=F (1). Включения могут оказаться равенствами. 5.2 Пусть Р с F, z1, z2 Î F. Рассм. P1=P(z1)- простое расширение Р. Р1 с F, P1(z2)=P(z1)(z2). Т 5.3 Пусть Р – подполе поля F. Z1, z2 ÎF. Р(z1)(z2)= Док-во: M c P(z1;z2); f(x;y) = g(x;y) x=z1 f(z1;y)= f(z1;z2)= g(z1;z2)=
Возьмём произвольный эл-т из P(z1)(z2) t= t Домножим числитель и знаменатель на общий знаменатель дробей, который получается в результате сложения
По определению P[x;y]=P(x)(y)
Р(z1) Св-во 5.4 Пусть Р – подполе F. Z1, z2 Тогда P(z1;z2)=P(z2;z1) Док-во: Р(z2;z1)= Поэтому М=М1. Отсюда P(z1)(z2)=P(z2;z1). Это расширение обозначим P(z1;z2) и назавём расширением Р,с порождающими z1, z2. Опр. 5.5. Аналогично предыдущему, если дано включение полей P c F, z1, z2
Алгебраические расширения. Опр.6.1 Пусть Р с F. Расширение F наз. Алгебраическим расширением Р, если Пр 6.2.1 R с C, z= a+bi; a, b Î R. f(x) =(x-(a+bi))(x-(a-bi))=((x-a)-bi)((x-a)+bi)=(x-a)2-(bi)2 = x2-2ax+(a2+b2) f(a+bi)=0
C является алгебраическим расширением R. Пр.6.2.2 Q c Q[ a+b (x-(a+b Т 6.3. Д-во: Пусть дано P c F. [F:P]=n. Возьмём (n+1) эл-тов dim Т.е. произвольный эл-т из F является алгебраическим над Р, значит F- алгебраическое расширение Р. Следствие6.4. Пусть дано расширение P c F, z Следствие6.5. Р(z) - алгебраическое расширение Р. Пусть z – алгебр. эл-т над P => Тогда по 6.4. расширение P(z) поля Р – конечно. Св-во 6.6. Пусть дано расширение P c F, z1,z2 Док-во: P c P(z1) c P(z1)(z2) c F. z1 – алгебр. эл-т над P=> deg [P(z1):P] =m = deg p(x) z2 – алгебр. эл-т над P1=> deg [P1(z2):P1] =k deg p1(x) где р(х) – min эл-т z2 над Р1. [P(z1)(z2):P]= [P(z1)(z2):P(z1)]
P c P(z1)(z2) – его степень над Р =mk, т.е. она конечна, зн. она алгебр. над P. z2
|
||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 449; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.71.21 (0.01 с.) |

 - расширение поля
- расширение поля  и z
и z 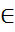
 =
= 
 подполе
подполе  Эл-т z
Эл-т z  такой ненулевой многочлен
такой ненулевой многочлен  , что f(z)=0 (является корнем f(x)). Если эл-т не является алгебраическим, то его называют трансцендентным над
, что f(z)=0 (является корнем f(x)). Если эл-т не является алгебраическим, то его называют трансцендентным над 
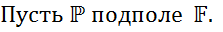 Рассм.
Рассм.  , то говоря, что
, то говоря, что  ] – степень расширения.
] – степень расширения. .
. ]=m базис
]=m базис 


 ]=n базис
]=n базис 

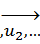

 , i=1,
, i=1, 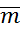 , j=1,
, j=1,  является базис расширения.
является базис расширения. ]=m
]=m  n=[
n=[ 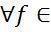
 ,
, 
 - базис
- базис 



 ,
, 


 Но
Но 

 – это базис над
– это базис над 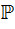 => лин. независим. Это означает, что для
=> лин. независим. Это означает, что для 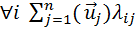

 значит для лин. независим =>
значит для лин. независим => 
 =0 => тривиальная лин. комбинация => лин. независ.
=0 => тривиальная лин. комбинация => лин. независ.

 B-C=0 B=C B=1
B-C=0 B=C B=1 , где f(x)
, где f(x) 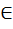 Q[x], g(x)
Q[x], g(x)  f- алгебраический над Q.
f- алгебраический над Q.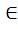 Q[x] – минимальный многочлен а. Т.к. g(a))
Q[x] – минимальный многочлен а. Т.к. g(a)) 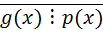 . Т.к. р(х) – неприводим, то р(х) и g(x)- взаимнопросты, НОД(р(х);g(x))=1. По критерию взаимной простоты u(x)
. Т.к. р(х) – неприводим, то р(х) и g(x)- взаимнопросты, НОД(р(х);g(x))=1. По критерию взаимной простоты u(x) 
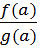 =
= 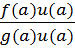 =
=  =h(a);
=h(a);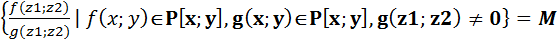
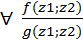
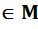 ; f(x;y)
; f(x;y) 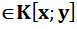
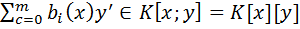
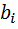 (x)
(x) 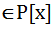 ,
, 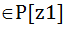

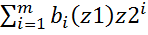
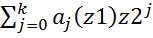
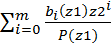

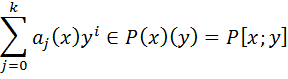
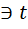
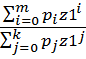 (*)
(*) , все
, все 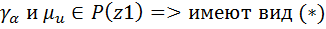
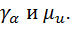 Получим, что в числителе и знаменателе из Р1=Р(z1) на степени элементов z2
Получим, что в числителе и знаменателе из Р1=Р(z1) на степени элементов z2 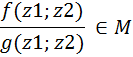
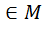
 .
.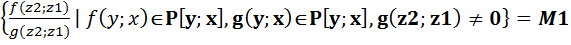
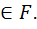 Рассм. P(z1,z2,….,zk), кот. наз. Расширением поля P c конечным числом (сk) пораждающих.
Рассм. P(z1,z2,….,zk), кот. наз. Расширением поля P c конечным числом (сk) пораждающих.
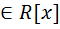
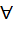 комплексное число явл. корнем многочлена с комплексными коэффициентами, значит
комплексное число явл. корнем многочлена с комплексными коэффициентами, значит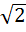 ]
]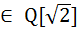
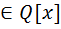

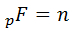 . Значит 1,
. Значит 1,  - линейно зависим. над Р. Это значит
- линейно зависим. над Р. Это значит 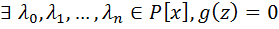
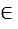 F, z – алгебр. эл-т над P. => Р(z) - алгебраическое расширение Р.
F, z – алгебр. эл-т над P. => Р(z) - алгебраическое расширение Р. такой, что р(х) – min z. В таком случае [P(z):P]= deg p(x)
такой, что р(х) – min z. В таком случае [P(z):P]= deg p(x) – алгебр. эл-т над P, a z2 - алгебр. эл-т над P1=P1(z1). Тогда z2- алгебраичен над Р.
– алгебр. эл-т над P, a z2 - алгебр. эл-т над P1=P1(z1). Тогда z2- алгебраичен над Р.