
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Минимальные алг. Элементов и их свойстваСодержание книги
Поиск на нашем сайте
Поле Опр. 1.1 Пусть Х-непустое мн-во,будем говорить,что на Х задана бинарная алг. Операция,если для Опр. 1.2 Бинарная операция Опр. 1.3 Пусть на непустом мн М задана ассоц.опер. Опр. 1.4 если в моноиде <M, Опр.1.5 Пусть <M, Опр. 1.6 Пусть на непустом мн К задана бинарная алг.опер <K;+>-коммут.группа(аддитивная тоже);<K; Если операц. умнож в К-коммут,то кольцо К наз. коммут.Если в кольце К есть еденица,то кольцо К наз кольцом с еденицей Опр.1.7 если в кольце К,кот комм.и с еденицей,у каждого ненулевого эл-та сущ обратный,то тогда К наз полем Опр. 1.8 Пусть F-поле,PсF,кот само явл полем относ операции слож и умнож кот Опр. 1.9 Пусть Р-некот.поле, V≠ 1) 2) 8) 3) Слож коммут 0) определено умнож в скалярах(эл-тов из Р) на векторы (эл-ты из Р) т.е. 5) 7) Тогда говорят,что Опр. 1. 10 Пусть F-поле,непустое подмножество Р наз подполем поля F,если само явл полем отномит тех операций которые сущ в F,в этом случае еще говорят,что F явл расширением поляР 2-3 Простое расширение поля. Опр 2.1. Пусть Р-подполе в F, РсА и z Теор. 2.2 В условиях опр 2.1 Р(z) явл полем и это найм подполе а F,содержит Р и эл-т z Опр 2.3 Р(z) наз простым расширением поля Р с помощью примитивного элемента z Прим2.4 P=Q F=К z= Q(
Опр. 2.5 Пусть РсF,эл-т z
Опр.2.6 PcF. Расширение P(z) наз простым алг расширением,если эл-т z алгебр над Р и трансцинд,если z-трансцинд над Р 1.1.Простое расширение поля. Пусть P[x] — кольцо полиномов от x над полем P, где P — подполе поля F. Напомним, что элемент a поля F называется алгебраическим над полем P, если a является корнем какого-нибудь полинома положительной степени из P [x]. Определение. Пусть P < F и a0F. Простым расширением поля P с помощью элемента a называется наименьшее подполе поля F, содержащее множество Р и элемент a. Простое расширение P с помощью a обозначается через P (a), основное множество поля P (a) обозначается через Р(a). Пусть a0F, P [x] — кольцо полиномов от x и P[x]={f(a)*f0P[x]},т. е. P [a] есть множество всех выражений вида a0 + a 1 a+...+ anan, где а0, a1,...an0P и n — любое натуральное число. Теорема 1.1. Пусть P [x]— кольцо полиномов от х над P и P (a)— простое расширение поля P. Пусть y — отображение P[x] на P[a] такое, что y(f)=f(a) для любого f из P[x]. Тогда: (а) для любого а из Р y (а) = а; (b) y(x) = a; (с) y является гомоморфизмом кольца P [x] на кольцо P [a]; (d) Ker y ={f0P[x]*f(a)=0}; (е) фактор-кольцо P [x]/Кег y изоморфно кольцу P [a]. Доказательство. Утверждения (а) и (Ь) непосредственно следуют из определения y. Отображение y сохраняет главные операции кольца P [x], так как для любых f и g из P[x] y(f + g)=f(a)+g(a), y(fg)= f(a)g(a), y(1)=1. Далее, по условию, y есть отображение Р[х] на Р[a]. Следовательно, y является гомоморфизмом кольца P [x] на кольцо P [a]. Утверждение (d) непосредственно следует из определения отображения y.Поскольку y — гомоморфизм кольца P [x] на P [a], то фактор-кольцо P[x]/Кег y изоморфно кольцу P [a]. Следствие 1.2. Пусть a — трансцендентный элемент над полем P. Тогда кольцо полиномов P [x] изоморфно кольцу P [a]. Доказательство. В силу трансцендентности a над P Kery={0}. Поэтому P[x]/{0}– P [a]. Кроме того, фактор-кольцо кольца P [x] по нулевому идеалу изоморфно P [x]. Следовательно, P [x]– P [a]. ТЕОРЕМА(о строении простого расширения с примитивным алгебраическим элементом):
Тогда
P(z) g(z)u(z)+p(z)v(z)=1, но p(z)=0
Конечное расширение поля. Пусть P — подполе поля F. Тогда мы можем рассматривать F как векторное пространство над P, т. е. рассматривать векторное пространство F + {
Определение. Расширение F поля P называется конечным, если F, как векторное пространство над P, имеет конечную размерность. Эта размерность обозначается через [F: P]. Cв-во 2.1. Если a — алгебраический элемент степени n над P, то [P (a):P]=n.Это свойство непосредственно следует из теоремы (Пусть a — алгебраический над полем P элемент положительной степени n. Тогда любой элемент поля P(a) однозначно представим в виде линейной комбинации n элементов 1, a,..., an-1 с коэффициентами из Р.). Определение. Расширение F поля P называется алгебраическим, если каждый элемент из F является алгебраическим над P. Теорема 2.2. Любое конечное расширение F поля P является алгебраическим над P. Доказательство. Пусть n-размерность F над P. Теорема, очевидно, верна, если n = 0. Предположим, что n>0. Любые n+1 элементов из F линейно зависимы над P. В частности, линейно зависима система элементов 1, a,..., an, т. е. существуют в P такие элементы с0, с1,…,cn не все равные нулю, что с01+ с1a+…+cn an = 0. Следовательно, элемент a является алгебраическим над P. Отметим, что существуют алгебраические расширения поля, не являющиеся конечными расширениями. Теор.2.7 Конечное расширение конечного расширения явл конечным Пусть F — конечное расширение поля L и L — конечное расширение поля P. Тогда F является конечным расширением поля P и [F: P] = [F: L][ L: P]. Доказательство. Пусть(1) a1,…,am — базис поля L над P (как векторного пространства) и (2) Коэффициенты 1k можно линейно выразить через базис (1):(4) lk = p1k a +…+ pmk am (pik где cik 0 P. Так как система (2) линейно независима над L, то из (5) следуют равенства (6) с1ka 1+...+сmka m = 0 (k = 1,..., n). Поскольку элементы a1,..., am линейно независимы над P, то из (6) следуют равенства c1k = 0,…,cmk = 0 (k = 1,..., n),показывающие, что все коэффициенты в (5) равны нулю. Таким образом, система элементов B линейно независима и является базисом F над P.Итак установлено, что [F, P] = nm = [F: L][L: P]. Следовательно, F является конечным расширением поля P
Конечно порождённые расширения. Определения и строение. Опр.5.1 Пусть заданы вложения полей Р с Т с F (1)’. Тогда (1) наз. цепочкой расширения. P=P1 c P2 c…c Pz=F (1). Включения могут оказаться равенствами. 5.2 Пусть Р с F, z1, z2 Î F. Рассм. P1=P(z1)- простое расширение Р. Р1 с F, P1(z2)=P(z1)(z2). Т 5.3 Пусть Р – подполе поля F. Z1, z2 ÎF. Р(z1)(z2)= Док-во: M c P(z1;z2); f(x;y) = g(x;y) x=z1 f(z1;y)= f(z1;z2)= g(z1;z2)=
Возьмём произвольный эл-т из P(z1)(z2) t= t Домножим числитель и знаменатель на общий знаменатель дробей, который получается в результате сложения
По определению P[x;y]=P(x)(y)
Р(z1) Св-во 5.4 Пусть Р – подполе F. Z1, z2 Тогда P(z1;z2)=P(z2;z1) Док-во: Р(z2;z1)= Поэтому М=М1. Отсюда P(z1)(z2)=P(z2;z1). Это расширение обозначим P(z1;z2) и назавём расширением Р,с порождающими z1, z2.
Опр. 5.5. Аналогично предыдущему, если дано включение полей P c F, z1, z2
Алгебраические расширения. Опр.6.1 Пусть Р с F. Расширение F наз. Алгебраическим расширением Р, если Пр 6.2.1 R с C, z= a+bi; a, b Î R. f(x) =(x-(a+bi))(x-(a-bi))=((x-a)-bi)((x-a)+bi)=(x-a)2-(bi)2 = x2-2ax+(a2+b2) f(a+bi)=0
C является алгебраическим расширением R. Пр.6.2.2 Q c Q[ a+b (x-(a+b Т 6.3. Д-во: Пусть дано P c F. [F:P]=n. Возьмём (n+1) эл-тов dim Т.е. произвольный эл-т из F является алгебраическим над Р, значит F- алгебраическое расширение Р. Следствие6.4. Пусть дано расширение P c F, z Следствие6.5. Р(z) - алгебраическое расширение Р. Пусть z – алгебр. эл-т над P => Тогда по 6.4. расширение P(z) поля Р – конечно. Св-во 6.6. Пусть дано расширение P c F, z1,z2 Док-во: P c P(z1) c P(z1)(z2) c F. z1 – алгебр. эл-т над P=> deg [P(z1):P] =m = deg p(x) z2 – алгебр. эл-т над P1=> deg [P1(z2):P1] =k deg p1(x) где р(х) – min эл-т z2 над Р1. [P(z1)(z2):P]= [P(z1)(z2):P(z1)]
P c P(z1)(z2) – его степень над Р =mk, т.е. она конечна, зн. она алгебр. над P. z2
Поле алгебраических чисел. Лемма 7.1. Пусть Р c F и u, v Из § 6(Алгебраические расширения) => P(u;v) – конечное алгебраическое расширение поля Р, значит все эл-ты из расширения P(u;v) алгебраичны над Р => P(u;v) с К (подмножество). Т. 7.2 В обозначениях Леммы 7.1 К является полем. Док-во: Возьмём u+v u-v K – замкнуто относительно сложения и умножения эл –тов 1 u 0
Аксиомы ассоциативности, коммутативности и дистрибутивности выполняются в К так как они выполняются в F => К – поле. Р с Обозначение 7.3. В обозначении 7.2 и 7.2 К= Обозначение 7.4. Т.к. имеет место расширение Q c R. Тогда Q c C => Алгебраическое замыкание
Имеем Q c
[Q( Q( линейно независ. Получим [
T.7.7 Док-во: Возьмём р(x)= a0, а1x,…., аnxn Т.к. поле С комплексных чисел алгебраически замкнуто, то Эл-ты a0, а1,…., аn Следствие 7.8 Пусть поле Р является алгебраическим замыканием поля F. Тогда алгебраическое замыкание Док-во: В предыдущем док-ве заменить Q Опр.7.9 Р с Т f – корень g(x) f – алгебраичен над Т => T c F - алгебр.. 2) Пусть Р с Т и Т с F - алгебраические. Т с F => f – корень g(x)= a0, а1x,…., аnxn a0, а1,…., аn – алгебраические над Р. Тогда по 6.8. Р(a0, а1,…., аn)[x] и f - корень g(x), то f – алгебраический над Р(a0, а1,…., аn). Имеем Р(a0, а1,…., аn)(f) ⊃ Р(a0, а1,…., аn) с помощью примитивного алгебраического эл-та. Это расширение конечное Р(a0, а1,…., аn)⊃Р Следствие: Алгебраическое расширение алгебраического расширения явл. алгебраическим расширением. Р с Т – алгебраическое расширение и Т с F – алгебраическое расширение => Р c F - алгебраическое расширение. Опред. Пусть дана группа <G;◦> и H<G. Введем на G бинарное отношение(~н) определив g1~H g2 тогда и только тогда, когда g1-1◦g2 из Н.
Теорема. Бинарное отношение ~Н на G из определения является отношением эквивалентности. Док-во: 1) Рефлексивность Для любого х, х ϸ х, где ϸ=~Н, х=g из G Для любого g, g~H g тогда и только тогда, когда для любого g, g-1◦g=e из Н. 2) Симметричность Для любых х,у (х ϸ у) следует у ϸ х Для любых g1, g2 g1~H g2 следует g2~H g1 g1~H g2 ↔ g1-1◦g2 из Н ↔│Н-группа│↔(g1-1◦g2)-1 из Н ↔g2-1◦g1-1 из Н ↔g2-1◦g1 из Н ↔g2~H g1 Транзитивность Для любых x,y,z (x ϸ y и y ϸ z) следует х ϸ z Для любых g1, g2, g3 g1~H g2 и g2~H g3 cледует g1~H g3 -? g1~H g2 и g2~H g3 ↔g1-1◦g2 из Н↔g2-1◦g3 из Н→(т.к. Н<G)→(g1-1◦g2)◦(g2-1◦g3) из Н→ g1-1◦((g2◦g3-1)◦g3)=g1-1◦(e◦g3) из Н→g1-1◦g3 из Н→g1~H g3 © Опред. Фактор-множество группы G относительно эквивалентности ~Н -- G/~Н-фактор-множество группы G по подгруппе Н.
Гомоморфный образ подгруппы ОПРЕД.: Пусть даны две группы <G1;◦>, <G2;
Св-во. Гомоморфный образ подгруппы является подгруппой. Док-во. Пусть дан гомоморфизм <G1, °>; <G2,*> — группа. f: G1 ®G2 — гомоморфизм, то тогда
H1<G1Þf (H1)<G2. f (H1)={f(h1)/h1 Композиция гомоморфизмов Композиция гомоморфизмов групп является гомоморфизмом групп. <G1, °>; <G2,*>, <G3, f:G1→G2 h:G2→G3 — гомоморфизм, тогда h°f ÷G1→G3— гомоморфизм. Док-во. h°f, G1→G3 — определено.
29.Изоморфизм групп. Определения, примеры, простейшие свойства. Опр. 12.1 Если отображение f из <G1, °>; <G2,*> — группы. f:G1®G2 — гомоморфизм, инъективно, то гомоморфизм f— вложение G1 в G2. Опр. 12.2 Если в <G1, °>; <G2,*> — группы. f: G1 ®G2 — гомоморфизм, отображение f является сюръективным, то гомоморфизм f называется эпиморфизмом. Опр.12.3 Если гомоморфизм <G1, °>; <G2,*> — группы. f: G1 ®G2 — гомоморфизм, является и вложением, и эпиморфизмом, то группы G1, G2 называются изоморфными при помощи изоморфизма f. Или пишут: G1 Св-во. 12.6 Каждая группа изоморфна сама себе. Док-во. Пусть дана группа <G1, °>. Докажем, что G1 Id:G1→G1; x→x (тождественное отображение). id (g1 °g1~)= g1 °g1~=id(g1)°id(g1~) (сохраняет операцию). Заметим, что id —биекция. Теорема.12.7 Пусть даны группы <G1, °>; <G2,*>, G1 Док-во. По условию f: G1 ®G2 —изоморфизмÞf—биекцияÞ
Теорема.12.8 Отношение «быть изоморфным» является отношением эквивалентности на множестве групп. Док-во. 1)рефлексивность 2)симметричность 3)транзитивность Теорема 12.9 Пусть f: G1 ®G2 — вложение. Тогда f1: G1 ® f (G1 ): x→f(x), (т.е. Док-во. 1) отображение f1 инъективно. X1 2) f1 сюръекция Þ f1 — изоморфизм. Свойства вложений групп Св-во: Пусть f:G1→G2 вложение. Тогда отображение f1:G1→Imf(Imf∙f(G1)∙{f(g1),g1 Док-во: Знаем, что если G1 подгруппа G2, то f(G1<G2) Imf<G2 g1
Теорема Лагранжа Лемма: G-группа,Н-подгруппа,тогда для любого g принадл. G отображение lg:H является биекцией.Док-во: lg-отображение,инъекция; пусть h1 lg-сюрьекция?для любого g°h принадлежит Опр. Если Теорема Лагранжа: G-конечная группа, |G| =m, H⁄G, |H|= h, [G:H]=к,тогда |G|=|H|*[G:H] или m=n*k(порядок группы=произв. порядка подгруппы на ее индекс) Док-во: т.к явл. отношением эквивалентности, при этом для любого g принадл. G, g с чертой= g°H, то левые смежные классы по подгруппе H задают разбиение множества G, т.е G= g1 °H Модуль G=модуль g1 °H∪g2°H∪…∪gк°H отсюда |G|= |g1°H|+ |g2°H|+..+ |gк°H|,но по лемме gi°H = |H| след-но m=n+n+n+…+n(k-раз) Следствие: m=n*k порядок подгруппы в конечной группе делит порядок подгруппы. Группа подстановок S(M)-группа подстановок на множестве М,если во множестве М=n элементов, то S(M)=sim(n)симметрическая группа на мн-ве из n элементов.Элементы из S(M)-подстановка элем.мн-ва. Теорема: Пусть G конечная группа,модуль G=n, тогда существует G1< 1) lg-биекция.Инъективность х1 2) lg-сюрьекция: для любого у принадлежит G: то lg(х)= у, g*x=у,то х= g-1*у, lg(g-1*у)=у 3)lg-биекция.cлед-но для любого g принадл. G, lg принадл.S(G)отображение F:G Для любого g1, g2 F(g1,*g2)= F(g1) Для любого x: F(g1,*g2)(x)- lg1*g2(x)= (g1*g2)*x=F(g1*g2)(x) знач. F(g1,*g2)= F(g1)° F(g2) F-инъективный гомоморфизм,т.е F вложение. Cтепени элементов в группе Опр. Пусть <G, n пррнадл.N, n<0, n=-n1, n1 | |||||||
|
| Поделиться: |

 х,у
х,у  Х задан элемент х
Х задан элемент х  у
у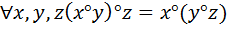 , если опер. Ассоц,то <X,
, если опер. Ассоц,то <X,  > наз. подгруппой
> наз. подгруппой наз нейтральным, если
наз нейтральным, если  если операция обозн. «+» и наз сложением,то тогда эл-т е наз нулевым,если операция обозн «
если операция обозн. «+» и наз сложением,то тогда эл-т е наз нулевым,если операция обозн «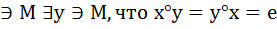 ,то эл-т у наз. симметричным эл-ту х;если операция «+»,то эл-т у наз противоположным эл-ту х и обозн у=-х;если операция «
,то эл-т у наз. симметричным эл-ту х;если операция «+»,то эл-т у наз противоположным эл-ту х и обозн у=-х;если операция « )
) ,то тогда К-наз кольцом
,то тогда К-наз кольцом в F,тогда говорят,что Р-подполе поля F или,что F явл расширением поля Р
в F,тогда говорят,что Р-подполе поля F или,что F явл расширением поля Р зада бинарная опер слож на 0
зада бинарная опер слож на 0 1) слож ассоц
1) слож ассоц 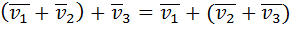
 1
1 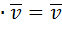
 =
= 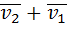 3)
3)  4)
4) 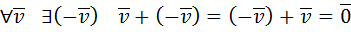

 6 )
6 ) 
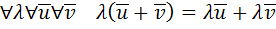
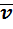 явл линейным(векторным)пространством над Р
явл линейным(векторным)пространством над Р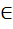 F.Будем обозначать P(z)={
F.Будем обозначать P(z)={  /
/ 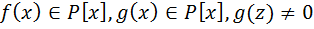 }
}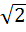
 }
} ={a+b
={a+b 
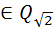
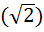 f(x)=a+bx g(x)=1
f(x)=a+bx g(x)=1 Ввиду минимальности расширения
Ввиду минимальности расширения 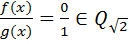
 наз алгебраическим над Р,если сущ многочлен f(x)
наз алгебраическим над Р,если сущ многочлен f(x)  такой,что f(x)
такой,что f(x) 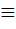 0 и при этом f(z)=0.Если элемент z не явл алгебраич над Р,то он наз трансцендентным над Р
0 и при этом f(z)=0.Если элемент z не явл алгебраич над Р,то он наз трансцендентным над Р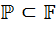 , z – алгебраический над
, z – алгебраический над 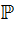 , p(x) – min полином z.
, p(x) – min полином z.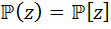 , где
, где 
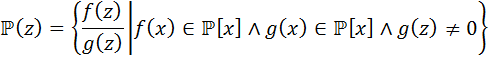
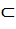 P(z), f(x)=f(z)/1
P(z), f(x)=f(z)/1 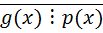 , но НОД(g(x),p(x))=1
, но НОД(g(x),p(x))=1 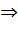 существуют u(x),v(x)
существуют u(x),v(x) 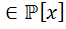 ,g(x)u(x)+p(x)v(x)=1
,g(x)u(x)+p(x)v(x)=1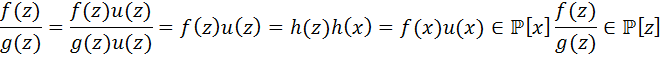
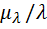 0P},где
0P},где  - операция умножения элементов из F на скаляр
- операция умножения элементов из F на скаляр  0P.
0P.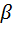 1,…,
1,…, 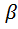 1+...+ln
1+...+ln  L).
L).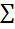 pik ai
pik ai 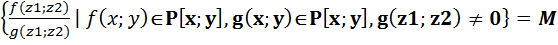
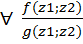
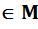 ; f(x;y)
; f(x;y) 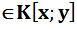
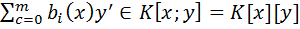
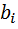 (x)
(x) 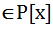 ,
, 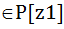

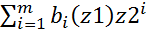
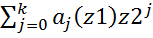
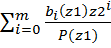

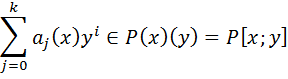
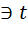
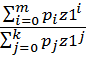 (*)
(*) , все
, все 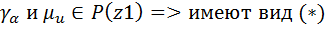
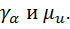 Получим, что в числителе и знаменателе из Р1=Р(z1) на степени элементов z2
Получим, что в числителе и знаменателе из Р1=Р(z1) на степени элементов z2 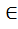 F2
F2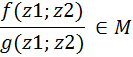
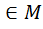
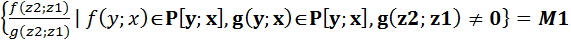
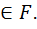 Рассм. P(z1,z2,….,zk), кот. наз. Расширением поля P c конечным числом (сk) пораждающих.
Рассм. P(z1,z2,….,zk), кот. наз. Расширением поля P c конечным числом (сk) пораждающих.
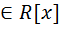
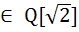
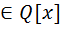

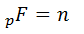 . Значит 1,
. Значит 1,  - линейно зависим. над Р. Это значит
- линейно зависим. над Р. Это значит 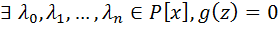
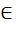 F, z – алгебр. эл-т над P. => Р(z) - алгебраическое расширение Р.
F, z – алгебр. эл-т над P. => Р(z) - алгебраическое расширение Р. такой, что р(х) – min z. В таком случае [P(z):P]= deg p(x)
такой, что р(х) – min z. В таком случае [P(z):P]= deg p(x) – алгебр. эл-т над P, a z2 - алгебр. эл-т над P1=P1(z1). Тогда z2- алгебраичен над Р.
– алгебр. эл-т над P, a z2 - алгебр. эл-т над P1=P1(z1). Тогда z2- алгебраичен над Р.
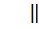
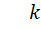
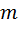
 (u,v - алгебраичны над
(u,v - алгебраичны над 
 Они принадлежат P(u;v), кот. само содержится в К. =>
Они принадлежат P(u;v), кот. само содержится в К. =>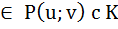
 u-1
u-1  (-u)
(-u) 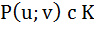 => Р с К – расширение полей.
=> Р с К – расширение полей.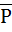 F и называется алгебраическим замыканием поля Р в поле F.
F и называется алгебраическим замыканием поля Р в поле F.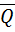 R – алгебраическое замыкание поля Q в поле R.
R – алгебраическое замыкание поля Q в поле R.
 ):Q]=n
):Q]=n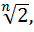
 ,…..,
,….., 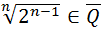 R
R R
R 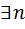 линейно независимых эл-тов на Q2.
линейно независимых эл-тов на Q2. [x], т.е. возьмём
[x], т.е. возьмём 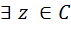 такое, что z- корень р(х).
такое, что z- корень р(х).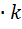 => оно алгебраическое расширение Q => z – алгебраический эл-т над Q => z
=> оно алгебраическое расширение Q => z – алгебраический эл-т над Q => z 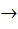 P, C
P, C 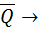
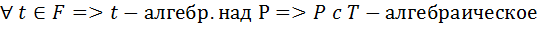 .
. 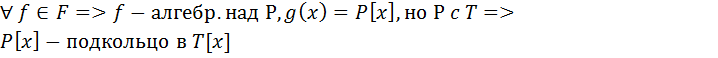 . (P[x] c T[x])
. (P[x] c T[x])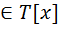
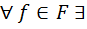 a0, а1,…., аn
a0, а1,…., аn  >. Гомоморфизм из группы G1 в G2 – отображение f:
>. Гомоморфизм из группы G1 в G2 – отображение f:  , которое «сохраняет операцию», т.е.
, которое «сохраняет операцию», т.е. 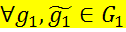
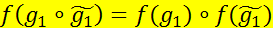
 H1}={h2|h2
H1}={h2|h2  сущ. h1|h1
сущ. h1|h1  f(H1) содержит f(h1) и f(H1)
f(H1) содержит f(h1) и f(H1)  f(h1~)Þh2-1*h2~
f(h1~)Þh2-1*h2~  >.
>.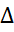 (h°f) g1~Þ (h°f)(g1°g1~)=h(f(g1°g1~))=/f—гомоморфизм/ =h(f(g1)*f(g1~))= /g2= f(g1), g2~=f(g1~)/=h(g2*g2~)= /h— гомоморфизм/ =h(g2)
(h°f) g1~Þ (h°f)(g1°g1~)=h(f(g1°g1~))=/f—гомоморфизм/ =h(f(g1)*f(g1~))= /g2= f(g1), g2~=f(g1~)/=h(g2*g2~)= /h— гомоморфизм/ =h(g2) 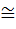 G2.
G2.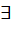 f -1: G2 ®G1. f -1 °f=idG1. f -1 —биекция. Покажем, что f -1сохраняет операцию
f -1: G2 ®G1. f -1 °f=idG1. f -1 —биекция. Покажем, что f -1сохраняет операцию g1, g1~ из G1/f(g1)=g2 и f(g1~)=g2~. Тогда имеем f -1(g2* g2~)= f -1 (f(g1)* f(g1~))=/ f —гомоморфизм/= f -1 (f(g1) ° f(g1~))=(f -1 °f)(g1° g1~)= =idG1(g1° g1~)= g1° g1~=/g1= f -1 (g2), g1~= f -1 (g2~)/= f -1 (g2) ° f -1 (g2~).
g1, g1~ из G1/f(g1)=g2 и f(g1~)=g2~. Тогда имеем f -1(g2* g2~)= f -1 (f(g1)* f(g1~))=/ f —гомоморфизм/= f -1 (f(g1) ° f(g1~))=(f -1 °f)(g1° g1~)= =idG1(g1° g1~)= g1° g1~=/g1= f -1 (g2), g1~= f -1 (g2~)/= f -1 (g2) ° f -1 (g2~).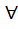 x
x 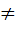 x1~ допустим f1(x1)= f1(x1~)Þf(x1)= f (x1~), что противоречит тому, что f инъективно. Значит f1(x1)
x1~ допустим f1(x1)= f1(x1~)Þf(x1)= f (x1~), что противоречит тому, что f инъективно. Значит f1(x1)  f1(x1~)
f1(x1~)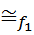 Imf)
Imf)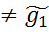 => f(g1)
=> f(g1) 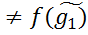 => f1(g1)
=> f1(g1)  инъекция
инъекция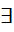 g1
g1 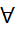 g1
g1  , f1(
, f1(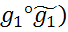 = f(
= f(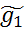 )=f1(g1)* f1(
)=f1(g1)* f1(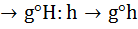
 , lg(h1)
, lg(h1)  (т.е не является инъекцией) g°h1= g°h2 тогда
(т.е не является инъекцией) g°h1= g°h2 тогда 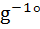 g°h1=g-1°g°h2 след-но h1= h2(противоречие);
g°h1=g-1°g°h2 след-но h1= h2(противоречие);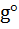 H, то lg(h)= g° h.
H, то lg(h)= g° h.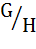 конечное множество и модуль G⁄H=k то число к –индекс подгруппы H в группе G.Обознач:[G:H]
конечное множество и модуль G⁄H=k то число к –индекс подгруппы H в группе G.Обознач:[G:H]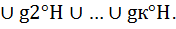
 такое,что G
такое,что G  <Sn.Док-во: для любого g принадл. G отображение lg: G → G:х
<Sn.Док-во: для любого g принадл. G отображение lg: G → G:х 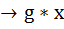 (умножение слева)
(умножение слева) , lg(х1)=lg(х2)отсюда g*х1= g*х2 тогда g-1°g°х1=g-1°g°х2, х1= х2(противоречие);
, lg(х1)=lg(х2)отсюда g*х1= g*х2 тогда g-1°g°х1=g-1°g°х2, х1= х2(противоречие); S(G):g
S(G):g 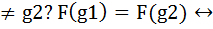 , lg1=lg2 след-но, lg1(е)=lg2(е) отсюда g*е= g*е тогда g1= g2(противоречие);Покажем, что сохраняет операцию:
, lg1=lg2 след-но, lg1(е)=lg2(е) отсюда g*е= g*е тогда g1= g2(противоречие);Покажем, что сохраняет операцию: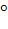 F(g2) отображение F:G→ G
F(g2) отображение F:G→ G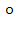 > g принадл. G, n принадл. Z,тогда n=0,то
> g принадл. G, n принадл. Z,тогда n=0,то  =е,
=е, =g
=g 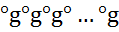 (n раз),
(n раз),


