
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Левые смежные классы элементов группы по подгруппе и классы эквивалентности.Содержание книги
Поиск на нашем сайте
ОПРЕД.: H<G, g ТЕОРЕМА: Левые смежные классы группы G по подгруппе H являются классами эквивалентности относительно отношения ͂H на G. g◦H= Д-во:g1 ОПРЕД.: Фактор-множество группы G относительно эквивалентности ͂H – G/ ͂H или G/H – фактор-множество группы G по подгруппе H. Пример: G=< Решение: 0◦H=0+4 1◦H=1+4 2◦H=2+4 3◦H=3+4
ОПРЕД.: Пусть дана группа <G;◦>, A СВОЙСТВО: Левый смежный класс g◦H группы G по подгруппе H элемента g равен произведению многочленов {g}◦H в смысле предыдущего опред.
22. Нормальные делители группы. Операции со смежными классами по нормальному делителю. Корректность определения операции. ОПРЕД.: Пусть <G;◦> - группа, x ОПРЕД.: Пусть <G;◦> - группа, подмножество N 1) N<G 2) СВОЙСТВО: <G;◦> - группа, Ni G, i Д-во:1) 2) ОПРЕД.: Пусть <G;◦> - группа, N G, g1 Пример: 4 ТЕОРЕМА: предыдущее определение корректно, т.е. результат операции над классами не зависит от того, через каких представителей записаны эти классы. Д-во: 1 часть. Пусть
Причем слева – определение умножения класса или умножение двух множеств. 2 часть. Аналогично 1 части показываем 3 часть. Однако, по условию
Фактор-множество группы по нормальному делителю. ТЕОРЕМА: Фактор-множество G/N группы G по нормальному делителю N с введенной над ней операцией (правило умножения смежных классов по N) является группой. Д-во: 1) ассоциативность
2)нейтральный в G/N – это
3)симметричный к
24. Гомоморфизмы групп. Определение, примеры, простейшие свойства. ОПРЕД.: Пусть даны две группы <G1;◦>, <G2;
ПРИМЕРЫ: 1)
Рассмотрим
Умножение матриц умножение чисел 2) Рассмотрим аддитивные группы
3)
СВОЙСТВО: При гомоморфизме образ нейтрального элемента является нейтральным. Т.е.
Д-во:
СВОЙСТВО: При гомоморфизме образ обратного элемента является обратным к образу данного. Т.е. если задан гомоморфизм (1), тогда Д-во:
Гомоморфный образ подгруппы ОПРЕД.: Пусть даны две группы <G1;◦>, <G2;
Св-во. Гомоморфный образ подгруппы является подгруппой. Док-во. Пусть дан гомоморфизм <G1, °>; <G2,*> — группа. f: G1 ®G2 — гомоморфизм, то тогда H1<G1Þf (H1)<G2. f (H1)={f(h1)/h1 Прообраз подгруппы при гомоморфизме Св-во. Пусть дан гомоморфизм <G1, °>; <G2,*> — группа. f: G1 ®G2 — гомоморфизм. H2<G2(f-1(H2)<G1). При гомоморфизме полный прообраз подгруппы явл. подгруппой. Док-во. f-1(H2)={h1/h1 h1 f(h1) Прообраз нормального делителя при гомоморфизме Св-во. Гомоморфный прообраз нормального делителя, является нормальным делителем. Пусть дан гомоморфизм <G1, °>; <G2,*> — группа. f: G1 ®G2 — гомоморфизм и N2 Док-во. Т.к. N2 h1 f(g1-1°n1°g1)=f(g1-1)*f(g1)*f(n1)=(f(g1))-1*f(n1)*f(g1) Композиция гомоморфизмов Композиция гомоморфизмов групп является гомоморфизмом групп. <G1, °>; <G2,*>, <G3, f:G1→G2 h:G2→G3 — гомоморфизм, тогда h°f ÷G1→G3— гомоморфизм. Док-во. h°f, G1→G3 — определено.
29.Изоморфизм групп. Определения, примеры, простейшие свойства. Опр. 12.1 Если отображение f из <G1, °>; <G2,*> — группы. f:G1®G2 — гомоморфизм, инъективно, то гомоморфизм f— вложение G1 в G2. Опр. 12.2 Если в <G1, °>; <G2,*> — группы. f: G1 ®G2 — гомоморфизм, отображение f является сюръективным, то гомоморфизм f называется эпиморфизмом. Опр.12.3 Если гомоморфизм <G1, °>; <G2,*> — группы. f: G1 ®G2 — гомоморфизм, является и вложением, и эпиморфизмом, то группы G1, G2 называются изоморфными при помощи изоморфизма f. Или пишут: G1 Св-во. 12.6 Каждая группа изоморфна сама себе. Док-во. Пусть дана группа <G1, °>. Докажем, что G1 Id:G1→G1; x→x (тождественное отображение). id (g1 °g1~)= g1 °g1~=id(g1)°id(g1~) (сохраняет операцию). Заметим, что id —биекция. Теорема.12.7 Пусть даны группы <G1, °>; <G2,*>, G1 Док-во. По условию f: G1 ®G2 —изоморфизмÞf—биекцияÞ
Теорема.12.8 Отношение «быть изоморфным» является отношением эквивалентности на множестве групп. Док-во. 1)рефлексивность 2)симметричность 3)транзитивность Теорема 12.9 Пусть f: G1 ®G2 — вложение. Тогда f1: G1 ® f (G1 ): x→f(x), (т.е. Док-во. 1) отображение f1 инъективно. X1 2) f1 сюръекция Þ f1 — изоморфизм. Свойства вложений групп Св-во: Пусть f:G1→G2 вложение. Тогда отображение f1:G1→Imf(Imf∙f(G1)∙{f(g1),g1 Док-во: Знаем, что если G1 подгруппа G2, то f(G1<G2) Imf<G2 g1
|
||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 377; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.255.247 (0.006 с.) |

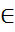 G. Левый смежный класс элемента g – множество g◦H={g◦h|h
G. Левый смежный класс элемента g – множество g◦H={g◦h|h  =[g] ͂H
=[g] ͂H g1
g1  Hg
Hg  h
h  >, H=4
>, H=4  ={4k|k
={4k|k  }. Найти: G/H
}. Найти: G/H



 ={
={  ,
,  }=(по опред.)=G/4Z={0+4
}=(по опред.)=G/4Z={0+4  G, A
G, A  ,
,  =B
=B  n
n  , тогда N=
, тогда N=  G
G Ni G (по условию)
Ni G (по условию)  Ni
Ni  (из 1-го пункта определения)
(из 1-го пункта определения) (т.к. Ni G)
(т.к. Ni G)  , т.к. N G
, т.к. N G – правило умножения смежных классов по N.
– правило умножения смежных классов по N.
 .Доказать,
.Доказать, 





 N
N 


 – истина.
– истина.
 , т.е. нужно доказать, что
, т.е. нужно доказать, что


 -
-  , т.е. нужно д-ть, что
, т.е. нужно д-ть, что 
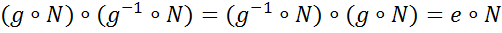


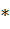 >. Гомоморфизм из группы G1 в G2 – отображение f:
>. Гомоморфизм из группы G1 в G2 – отображение f:  , которое «сохраняет операцию», т.е.
, которое «сохраняет операцию», т.е. 

 – мн-во невыраженных квадратных матриц размерности n x m,
– мн-во невыраженных квадратных матриц размерности n x m,  ;
; 
 , каждой матрице ставится в соответствие ее определитель.
, каждой матрице ставится в соответствие ее определитель.

 – верно.
– верно. и отображение
и отображение 


 – истина.
– истина. ,
,  зададим отображение
зададим отображение 


 – истина.
– истина. (1)
(1)


 >. Гомоморфизм из группы G1 в G2 – отображение f:
>. Гомоморфизм из группы G1 в G2 – отображение f:  , которое «сохраняет операцию», т.е.
, которое «сохраняет операцию», т.е. 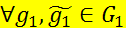
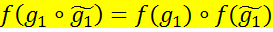
 сущ. h1|h1
сущ. h1|h1  f(h1~)Þh2-1*h2~
f(h1~)Þh2-1*h2~  G2Þ f-1 (N2)
G2Þ f-1 (N2)  <G1
<G1 >.
>.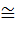 G2.
G2.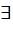 f -1: G2 ®G1. f -1 °f=idG1. f -1 —биекция. Покажем, что f -1сохраняет операцию
f -1: G2 ®G1. f -1 °f=idG1. f -1 —биекция. Покажем, что f -1сохраняет операцию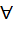 g2, g2~ f -1(g2*g2~)=f -1(g2)°f -1(g2~). Т.к.f—биекция, то
g2, g2~ f -1(g2*g2~)=f -1(g2)°f -1(g2~). Т.к.f—биекция, то  g1, g1~ из G1/f(g1)=g2 и f(g1~)=g2~. Тогда имеем f -1(g2* g2~)= f -1 (f(g1)* f(g1~))=/ f —гомоморфизм/= f -1 (f(g1) ° f(g1~))=(f -1 °f)(g1° g1~)= =idG1(g1° g1~)= g1° g1~=/g1= f -1 (g2), g1~= f -1 (g2~)/= f -1 (g2) ° f -1 (g2~).
g1, g1~ из G1/f(g1)=g2 и f(g1~)=g2~. Тогда имеем f -1(g2* g2~)= f -1 (f(g1)* f(g1~))=/ f —гомоморфизм/= f -1 (f(g1) ° f(g1~))=(f -1 °f)(g1° g1~)= =idG1(g1° g1~)= g1° g1~=/g1= f -1 (g2), g1~= f -1 (g2~)/= f -1 (g2) ° f -1 (g2~).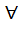 x
x 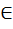 G1(f1(x))=f(x)) то тогда f1 является изоморфизмом групп G и f(G1).
G1(f1(x))=f(x)) то тогда f1 является изоморфизмом групп G и f(G1).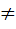 x1~ допустим f1(x1)= f1(x1~)Þf(x1)= f (x1~), что противоречит тому, что f инъективно. Значит f1(x1)
x1~ допустим f1(x1)= f1(x1~)Þf(x1)= f (x1~), что противоречит тому, что f инъективно. Значит f1(x1)  f1(x1~)
f1(x1~)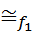 Imf)
Imf)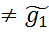 => f(g1)
=> f(g1) 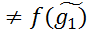 => f1(g1)
=> f1(g1)  инъекция
инъекция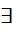 g1
g1 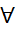 g1
g1  , f1(
, f1(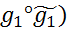 = f(
= f(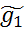 )=f1(g1)* f1(
)=f1(g1)* f1(


