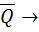Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгебраичность алгебраического расширения алгебраического расширения.Содержание книги
Поиск на нашем сайте
Следствие 6.6. Пусть элементы z1,z2 из F, где Р c F, алгебраичны над Док-во: Т.к. z1 – алгебр. над Р=>P(z1)- алгебр. конечное расширение над Р. z2 – алгебр. над Р=>P(z1)- т.к. P[x} c P(z1)[x]=> z2 - алгебр. над Р(z1), значит расширение P(z1)(z2) является конечным алгебраическим расширением поля P(z1).Тогда имеем цепочку конечных расширений P c P(z1) c P(z1)(z2). Т.к. конечное расширение конечных расширений явл. конечным расширением, то P c P(z1;z2) явл. конечным => алгебр.. Следствие 6.7. P c F, z1, z2,…..,zn Док-во: n=1 P(z1) – конечное алгебраич. n=k P(z1, z2,…..,zk) - конечное алгебраич. расшир. Р. n=k+1 P(z1, z2,…..,zk,zk+1) = P(z1, z2,…..,zk)(zk+1). Т.к. zk+1 алгебр. над P, то он алгебр. и над P(z1, z2,…..,zk). Тогда P(z1, z2,…..,zk)(zk+1)- простое расширение P(z1, z2,…..,zk) с помощью алгебр. эл-та zk+1 Имеем P(z1, z2,…..,zk,zk+1) Конечное расширение явл. алгебраическим. Св-во 6.8. Классы конечных и классы конечно порождённых алгебраических расширений совпадают. Док-во: Р с Т с F и [T:P]=n. z1, z2,….,zn – базис T над P. Т.к. Т – поле, то, очевидно, что Т= P(z1, z2,…..,zn) => Т – алгебраическое расширение Р. Пусть Т- конечно порождающее алгебраическое расширение Р. Тогда по 6.7. Т – конечно. Т. 6.9. Пусть дана цепочка расширений P c Т с F. Тогда расширение явл. алгебраическим тогда и только тогда, когда расширение Р с Т и Т с F - алгебраические. Док-во: 1) Пусть P c F – алгебр.. Р с Т
f – корень g(x) f – алгебраичен над Т => T c F - алгебр.. 2) Пусть Р с Т и Т с F - алгебраические. Т с F => f – корень g(x)= a0, а1x,…., аnxn a0, а1,…., аn – алгебраические над Р. Тогда по 6.8. Р(a0, а1,…., аn)[x] и f - корень g(x), то f – алгебраический над Р(a0, а1,…., аn). Имеем Р(a0, а1,…., аn)(f) ⊃ Р(a0, а1,…., аn) с помощью примитивного алгебраического эл-та. Это расширение конечное Р(a0, а1,…., аn)⊃Р Следствие: Алгебраическое расширение алгебраического расширения явл. алгебраическим расширением. Р с Т – алгебраическое расширение и Т с F – алгебраическое расширение => Р c F - алгебраическое расширение.
Поле алгебраических чисел. Лемма 7.1. Пусть Р c F и u, v
Из § 6(Алгебраические расширения) => P(u;v) – конечное алгебраическое расширение поля Р, значит все эл-ты из расширения P(u;v) алгебраичны над Р => P(u;v) с К (подмножество). Т. 7.2 В обозначениях Леммы 7.1 К является полем. Док-во: Возьмём u+v u-v K – замкнуто относительно сложения и умножения эл –тов 1 u 0
Аксиомы ассоциативности, коммутативности и дистрибутивности выполняются в К так как они выполняются в F => К – поле. Р с Обозначение 7.3. В обозначении 7.2 и 7.2 К= Обозначение 7.4. Т.к. имеет место расширение Q c R. Тогда Q c C => Алгебраическое замыкание Имеем Q c
[Q( Q( линейно независ. Получим [
T.7.7 Док-во: Возьмём р(x)= a0, а1x,…., аnxn Т.к. поле С комплексных чисел алгебраически замкнуто, то Эл-ты a0, а1,…., аn Следствие 7.8 Пусть поле Р является алгебраическим замыканием поля F. Тогда алгебраическое замыкание Док-во: В предыдущем док-ве заменить Q Опр.7.9 Р с Т f – корень g(x) f – алгебраичен над Т => T c F - алгебр.. 2) Пусть Р с Т и Т с F - алгебраические.
Т с F => f – корень g(x)= a0, а1x,…., аnxn a0, а1,…., аn – алгебраические над Р. Тогда по 6.8. Р(a0, а1,…., аn)[x] и f - корень g(x), то f – алгебраический над Р(a0, а1,…., аn). Имеем Р(a0, а1,…., аn)(f) ⊃ Р(a0, а1,…., аn) с помощью примитивного алгебраического эл-та. Это расширение конечное Р(a0, а1,…., аn)⊃Р Следствие: Алгебраическое расширение алгебраического расширения явл. алгебраическим расширением. Р с Т – алгебраическое расширение и Т с F – алгебраическое расширение => Р c F - алгебраическое расширение.
|
||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 283; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.252.50 (0.01 с.) |

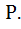 Тогда P(z1)(z2) = P(z1;z2) явл. алгебр. расширением Р.
Тогда P(z1)(z2) = P(z1;z2) явл. алгебр. расширением Р. . Тогда расширение P c P(z1;z2;……;zn) явл. конечным и алгебраичным расширением поля Р.
. Тогда расширение P c P(z1;z2;……;zn) явл. конечным и алгебраичным расширением поля Р. P(z1, z2,…..,zk) конечное, а по посылке индукции P(z1, z2,…..,zk) – конечное
P(z1, z2,…..,zk) конечное, а по посылке индукции P(z1, z2,…..,zk) – конечное 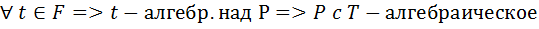 .
. 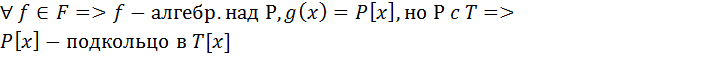 . (P[x] c T[x])
. (P[x] c T[x])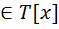
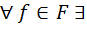 a0, а1,…., аn
a0, а1,…., аn 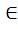 T, аn
T, аn  .
. (u,v - алгебраичны над
(u,v - алгебраичны над 
 Они принадлежат P(u;v), кот. само содержится в К. =>
Они принадлежат P(u;v), кот. само содержится в К. =>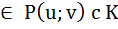
 (-u)
(-u) 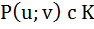 => Р с К – расширение полей.
=> Р с К – расширение полей. F и называется алгебраическим замыканием поля Р в поле F.
F и называется алгебраическим замыканием поля Р в поле F. R – алгебраическое замыкание поля Q в поле R.
R – алгебраическое замыкание поля Q в поле R.
 ):Q]=n
):Q]=n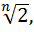
 ,…..,
,….., 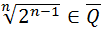 R
R R
R 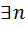 линейно независимых эл-тов на Q2.
линейно независимых эл-тов на Q2. [x], т.е. возьмём
[x], т.е. возьмём 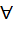 многочлен с коэффициентами из алгебраического замыкания.
многочлен с коэффициентами из алгебраического замыкания.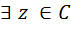 такое, что z- корень р(х).
такое, что z- корень р(х).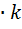 => оно алгебраическое расширение Q => z – алгебраический эл-т над Q => z
=> оно алгебраическое расширение Q => z – алгебраический эл-т над Q => z 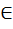
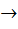 P, C
P, C