
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема: Определение смежных классов по Идеалу корректно.Содержание книги
Поиск на нашем сайте
Док. Если а+ a+ т.к. a=a+0=a b+y=b1+ ab=(a1+x)(b1+y)=a1b1+(a1y+b1x+yx) ab=ab+0 Значит(а1b1+ Смежные классы задают разбиение К1 значит они не не пересекаются или совпадают => Классы ровны a1b+
44.Фактор=кольца. Определение, примеры, свойства. Теорема: К кольцо, Док. <К/ 2.0.Выполним по опр. 2.1.а+ ((а+ (а+ 2.2.Возьмем (а+ (а+ 2.3.((а+ Пример:К=Z,
Свойство: Если К-ком. Кольцо, то К/ (а+ (а+ (1+
45. Главные идеалы. Кольца главных идеалов. Определение и примеры. Пусть К -кольцо, а из К. Обозначим (а)={k Док-во: k1 k1
Теорема: Кольцо Z – это кольцо главных идеалов, т.е. любой идеал в Z явл. Главным Док-во: Пусть I идеал в Z, возможны 2 случая 1) I={0}; I=(0) главный идеал нуля 2) I Рассмотрим все ненулевые элементы из I и их модули. Среди них выберем наименьшее а, по теореме о делении с остатком Для любого b из I, b=аq+r, где q,r r = b + (- q) a => r По выбору а, r не может быть натуральным, значит r = 0, значит b=a I = (a) Теорема: Пусть P поле. Тогда Р[х] – кольцо главных идеалов Док-во: Пусть I идеал Р[х] 1) I={0} тогда I=(0) 2) I Рассмотрим deg f(x), таких, что f(x) Для любого многочлена h(x) h(x)= f0(x) q(x), r(x) r(x)=h(x)+(-q(x)) f0(x) => r(x) по выбору f0(x), deg r(x) не может быть меньше f0(x) значит r(x) h(x)= f0(x)q(x)=>h(x) Теорема: Пусть К произвольное кольцо. А из К. Тогда множество I={k1a1+k2a2+…+ksas|ki Док-во: Возьмем k1a1+k2a2+…+ksas
k1a1+k2a2+…+ksas-( Для любого k из К k(k1a1+k2a2+…ksas)=(kk1)a1+(kk2)a2+…+(kks)as По критерию идеала I идеал. Св-во: К кольцо, I идеал. Тогда смежный класс а+I = I ó a Док-во: 1) а+I=I т.к. 0 2) a C другой стороны I=0+I (смежные классы или совпадают, или пересекаются) I и а+I – это смежные классы, не пересекаться они не могут, т.к. а+I C I значит они совпадают. Естесственный гомоморфизм кольца на его фактор-кольцо. Пусть <K1;+;
Опред: Гомоморфизм f колец наз. -- вложением, если f - инъекция; --эпиморфизмом, если f - сюръекция; -- изоморфизмом, если f - биекция. Св-во: Пусть К1 и К2 – кольца и f:K1
I2 – идеал, К2 Максимальные идеалы. Фактор-кольцо по максимальному идеалу. Опред: К -кольцо. Его идеал I наз. максимальным, если из того, что I1 идеал К такой, что I C I1 C K, следует, что I1=I или I1=K Пример: (6) С Z – не явл. максимальным. (6) С (2) С (Z) Теорема: В любом кольце К любой идеал I содержится в нек. максимальном идеале. Простые идеалы. Фактор-кольцо по простому идеалу. Определение: Пусть К кольцо, элемент а из К наз. делителем нуля если: 1) а Свойство: Обратимый элемент кольца не может быть делителем нуля (в частности в поле нет делителей нуля) Док-во: Пусть а обратим в кольце К, значит существует а-1 из К От противного Допустим что а делитель нуля, то есть существует b из К\{0} такое что b b b=0 противоречие Определение: Пусть К кольцо. Идеал I кольца К наз. простым, если, из того, что Свойство: Если I простой идеал кольца К, то К/I не имеет делителей нуля Док-во: От противного Пусть а+I и b+I Тогда (ab)+I=I ab a+I=0+I или b+I=0+I противоречие Св-во: К –кольцо, I – идеал, К/I без делителей нуля, следовательно идеал I простой идеал K. Св-во: Главный идеал nZ=(n) явл простым идеалом кольца Z ó n простое число.
|
|||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 333; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.71.146 (0.01 с.) |

 =а1+
=а1+  =>ab+
=>ab+ 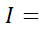 a1b1+
a1b1+ 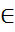 a+
a+ 
 a1b1+
a1b1+ 

 )
)  (ab+
(ab+  док.
док. фактор множества К/
фактор множества К/ 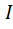 с операцией сложения и умножения классов является кольцом.
с операцией сложения и умножения классов является кольцом. b+
b+  из К/
из К/  )(b+
)(b+ 
 , Z/5Z
, Z/5Z -ком. Кольцо; Если К-кольцо с 1, то К/
-ком. Кольцо; Если К-кольцо с 1, то К/  a|k
a|k 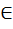 K} тогда (а) идеал К, который называется главным идеалом, порожденным элементом а.
K} тогда (а) идеал К, который называется главным идеалом, порожденным элементом а.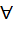 k
k 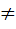 {0}
{0} , 0
, 0  r<a.
r<a. 0
0
 a1+
a1+ 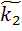 a2+…+
a2+…+  as
as 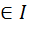 Для любого b
Для любого b  > и <K1;
> и <K1;  ;
;  > -кольца. Отображение f:K1
> -кольца. Отображение f:K1  K2 наз. гомоморфизмом колец, если оно сохраняет операцию, т.е.
K2 наз. гомоморфизмом колец, если оно сохраняет операцию, т.е.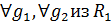


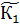 - подкольцо, К1
- подкольцо, К1  ) – подкольцо К1
) – подкольцо К1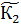 - подкольцо, К2
- подкольцо, К2 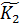 ) – подкольцо К1
) – подкольцо К1 ) – идеал К1
) – идеал К1 0, 2)
0, 2)  b из К\{0} такое что b
b из К\{0} такое что b 
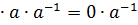
 , следует, что
, следует, что  или
или 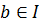
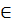 К/I\{0+I} и (а+I)(b+I)=0+I
К/I\{0+I} и (а+I)(b+I)=0+I => a
=> a 


