
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Св-ва эпоморфизмов групп . Каноническое отображение группы на её фактор-группы. (Естественный гомоморфизм).Содержание книги
Поиск на нашем сайте
Св-во 12.10 <G1, °>— группа, N—нормальный делитель G. Тогда <G/N, °>— фактор-группа. Тогда отображение f:G→ G/N; g → g° N является эпиморфизмом и Kerf=N. Док-во. f — задано. Докажем, что f(g1° g1~)=(g1° g1~)° N. f(g1) ° f(g1~)=(g1° N) ° (g1~° N)= (g1° g1~)° N. Доказать Kerf=N е° N= N е° N={ е° n/n Доказать N
Докажем, что Kerf c N Покажем, что x Опр.12.11 f:G→ G/N из св-ва 12.10 называется естественным гомоморфизмом группы G на фактор группе G/N. Св-во 12.12 Пусть дано <G1,°>; <G2,*> и отображение f: G1®G2 —эпиморфизм у которого N= Kerf, то тогда G1/N Док-во. F: G1/N®G2: g1° N®f(g1). Покажем, что F это отображение. Т.е.результат действия F на смежные классы не зависит от того, через каких представителей записаны эти классы. Пусть g1° N= g1~° N. Тогда g1— = g1~Þ g1 ~N g1~Þ g1-1 °g1~ Докажем, что F — гомоморфизм. F((g1° N) ° (g2° N))=F((g1° g2 )° N)=f(g1)*f(g2). F(g1° N)* F(g2° N)= f(g1)*f(g2). Т.к.правые части равны, то левые тоже равны.
Теорема Лагранжа Лемма: G-группа,Н-подгруппа,тогда для любого g принадл. G отображение lg:H является биекцией.Док-во: lg-отображение,инъекция; пусть h1 lg-сюрьекция?для любого g°h принадлежит Опр. Если Теорема Лагранжа: G-конечная группа, |G| =m, H⁄G, |H|= h, [G:H]=к,тогда |G|=|H|*[G:H] или m=n*k(порядок группы=произв. порядка подгруппы на ее индекс) Док-во: т.к явл. отношением эквивалентности, при этом для любого g принадл. G, g с чертой= g°H, то левые смежные классы по подгруппе H задают разбиение множества G, т.е G= g1 °H Модуль G=модуль g1 °H∪g2°H∪…∪gк°H отсюда |G|= |g1°H|+ |g2°H|+..+ |gк°H|,но по лемме gi°H = |H| след-но m=n+n+n+…+n(k-раз) Следствие: m=n*k порядок подгруппы в конечной группе делит порядок подгруппы. Группа подстановок S(M)-группа подстановок на множестве М,если во множестве М=n элементов, то S(M)=sim(n)симметрическая группа на мн-ве из n элементов.Элементы из S(M)-подстановка элем.мн-ва. Теорема: Пусть G конечная группа,модуль G=n, тогда существует G1< 1) lg-биекция.Инъективность х1 2) lg-сюрьекция: для любого у принадлежит G: то lg(х)= у, g*x=у,то х= g-1*у, lg(g-1*у)=у 3)lg-биекция.cлед-но для любого g принадл. G, lg принадл.S(G)отображение F:G Для любого g1, g2 F(g1,*g2)= F(g1) Для любого x: F(g1,*g2)(x)- lg1*g2(x)= (g1*g2)*x=F(g1*g2)(x) знач. F(g1,*g2)= F(g1)° F(g2) F-инъективный гомоморфизм,т.е F вложение. Cтепени элементов в группе Опр. Пусть <G, n пррнадл.N, n<0, n=-n1, n1 Теорема:Пусть G-группа,g принадл. G, n, m принадл. Z тогда
1)
1).m=0: gm °gn=g0 n=0: gm °gn =g0 ºgm=e° gm=gm=g0+m=gm+n m>0,n>0: gm °gn = (g°g°g°g°…°g) (g°g°g°g°…°g)= g°g°g°g°…°g=gm+n m<0, n<0: n=-n1,m=-m1: gm °gn =g-m1° g-n1= (g-1)m 1°(g-1)n1 = =(g-1)m1+n1=gm+n m<0, n<0,n=-n1: gm °gn =gm° g-n1= (gm)°(g-1)n1 = g°g°g-1g°…°g=A m=n1: A= g°g°g^(-1)g°…°g=ge=gm-n1=gm+n m>n1: A= (g°g°g^(-1)g°…°g)(m-n1раз)=gm-n1=gm+n m<n1: A= g°g°g^(-1)g°…°g=(g-1)n1-m=gm+n 2) g-m=(g-1)m=(gm)-1; m=0:g0=(g-1)0 m принадл N: g-m=(g-1)m gm (gm)-1=(g-1)m: (g-1)m
37. Доказать, что
Циклические подгруппы и группы. Подгруппа «g» называется циклической подгруппой группы G, порожденная элементом g (образующим g) Если в группе «G;◦» «G;◦» - группа, g Если элемент g группы G имеет конечный порядок, то наименьшее число Если Дак.: 1)
От противного:
|«g» |=
В любой конечной группе G порядок любого элемента делит порядок группы Дак.: |G|=m, g
Кольца Непустое множество А – кольцо, если на нем задана бинарная операция, обычно обозначаемая «+» и называемая сложением. Такая, что «К;+» - аддетивная камуттативная группа.
На К задана бинарная операция обозначаемая «*» и называемая умнажением, такая что «К;*»-полугруппа
Операция сложения и умножения в К согласованы условиями дистрибутивности т.е.
Кольцо К – коммуттативно если операция умножения коммуттативна т.е.
Кольцо К – кольцо с единицей если в нем
Прим: «Z;+;*» - комуттативное кольцо с 1 «5Z;+;◦» - коммуттативное кольцо без 1 «С;+; ◦» - кольцо
40. Подкольца. Определение, примеры, простейшие свойства. Критерий подкольца. Пусть «К;+;◦»-кольцо. Непустое подмножество К в К –подкольцо в К, если оно само является кольцом относительно операций в К. Критерий подкольца: «К;+;◦» - кольцо; К1 Доказательство: Если К1- подкальцо, тогда К1-оддитивная подгруппа в К, тогда п. 1;2 выполняются Обратно п. 1;2 – выполняются, тогда очивидно выполняются все пункты определения кольца т.к. они выполняются для всех элементов из К Примеры: 5Z- подкальцо в Z К= Mat(nxn;R) K1 = 41.Идеалы колец.Определение. Корректность определения. Опр. Пусть <К +, *> комутат. кольцо, 1. 2. Теорема1: 1. 2.
Критерий идеала. Док. Если Пусть 1 и 2 выполнимы k = b А пункт 2 показывает что Пример: В качестве К = Z, В качестве 1. К- любое кольцо К*0=0 Идеал 2. 3. К = Z, 4. K = Mat(2x2; R);
43.Операции с идеалом.Определение. Корректность определения. Опр. Пусть К кольцо Более того К/ <К/
(-k)+a+k=(-k)+k+a=0+a=a Опр. К-кольцо (а+
|
||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 397; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.23.101.75 (0.007 с.) |

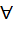 g1,g1~ f(g1° g1~)= f(g1) ° f(g1~)=(g1° g1~)° N.
g1,g1~ f(g1° g1~)= f(g1) ° f(g1~)=(g1° g1~)° N.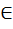 N}={n/n
N}={n/n  Kerf
Kerf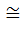 G2.
G2.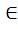 G2. Т.к.f— эпиморфизм
G2. Т.к.f— эпиморфизм 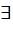 g1
g1 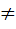 g1~° N, но F(g1° N)= F(g1~°N)Þf(g1)=f(g1~) /* f(g1-1 )/ Þ f(g1-1 )* f(g1)= f(g1-1 )* f(g1~)Þ f(g1-1 °g1)= f(g1-1 °g1~)Þf(e1)= f(g1-1 °g1~)Þ e2=f(g1-1 °g1~)Þg1-1 °g1~
g1~° N, но F(g1° N)= F(g1~°N)Þf(g1)=f(g1~) /* f(g1-1 )/ Þ f(g1-1 )* f(g1)= f(g1-1 )* f(g1~)Þ f(g1-1 °g1)= f(g1-1 °g1~)Þf(e1)= f(g1-1 °g1~)Þ e2=f(g1-1 °g1~)Þg1-1 °g1~  Þg1 ~N g1~ Þg1— =g1—~Þ g1° N= g1~° N — противоречие.
Þg1 ~N g1~ Þg1— =g1—~Þ g1° N= g1~° N — противоречие.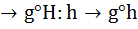
 , lg(h1)
, lg(h1)  (т.е не является инъекцией) g°h1= g°h2 тогда
(т.е не является инъекцией) g°h1= g°h2 тогда 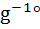 g°h1=g-1°g°h2 след-но h1= h2(противоречие);
g°h1=g-1°g°h2 след-но h1= h2(противоречие);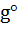 H, то lg(h)= g° h.
H, то lg(h)= g° h.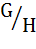 конечное множество и модуль G⁄H=k то число к –индекс подгруппы H в группе G.Обознач:[G:H]
конечное множество и модуль G⁄H=k то число к –индекс подгруппы H в группе G.Обознач:[G:H]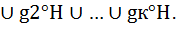
 такое,что G
такое,что G  <Sn.Док-во: для любого g принадл. G отображение lg: G → G:х
<Sn.Док-во: для любого g принадл. G отображение lg: G → G:х 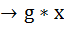 (умножение слева)
(умножение слева)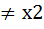 , lg(х1)=lg(х2)отсюда g*х1= g*х2 тогда g-1°g°х1=g-1°g°х2, х1= х2(противоречие);
, lg(х1)=lg(х2)отсюда g*х1= g*х2 тогда g-1°g°х1=g-1°g°х2, х1= х2(противоречие);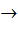 S(G):g
S(G):g 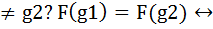 , lg1=lg2 след-но, lg1(е)=lg2(е) отсюда g*е= g*е тогда g1= g2(противоречие);Покажем, что сохраняет операцию:
, lg1=lg2 след-но, lg1(е)=lg2(е) отсюда g*е= g*е тогда g1= g2(противоречие);Покажем, что сохраняет операцию: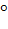 F(g2) отображение F:G→ G
F(g2) отображение F:G→ G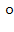 > g принадл. G, n принадл. Z,тогда n=0,то
> g принадл. G, n принадл. Z,тогда n=0,то  =е,
=е, =g
=g 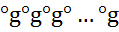 (n раз),
(n раз),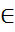 .N: gn=
.N: gn=  =
=  )n1 =(g-1)n1=g-1°g-1(n1 раз).
)n1 =(g-1)n1=g-1°g-1(n1 раз). ; 2) g-m=(g-1)m=
; 2) g-m=(g-1)m=  )-1; 3) (gm)n=(g)mn
)-1; 3) (gm)n=(g)mn −во:
−во: gn=eºgn =gn=g0+n=gm+n
gn=eºgn =gn=g0+n=gm+n e=e-1верно
e=e-1верно
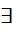 g
g  G, то G – циклическая группа с порождающим элементом g
G, то G – циклическая группа с порождающим элементом g =e. Если к
=e. Если к 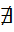 , то элемент g имеет бесконечный порядок.
, то элемент g имеет бесконечный порядок.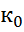 |
|  =e – порядок элемента g и обозначается
=e – порядок элемента g и обозначается  ;
;  ; …;
; …;  }
} «g» Разделим S на
«g» Разделим S на  =
=  ◦
◦  =
=  ◦
◦  =
=  {e=
{e=  =
=  0≤
0≤  ≤
≤  <
< 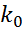
 =e
=e  N
N <
< 
 а, в а+в
а, в а+в  К1 – подкольцо в К ó 1) К1- аддитивная подгруппа в К; 2)
К1 – подкольцо в К ó 1) К1- аддитивная подгруппа в К; 2) 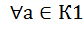
 а*в
а*в  К1
К1 где a,b,c
где a,b,c  непустое подмножество в К-идеалом кольца К если:
непустое подмножество в К-идеалом кольца К если: K*a
K*a 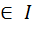 (Если
(Если  k
k  K*a
K*a  по критерию подкольца
по критерию подкольца  это подкольцо в К.
это подкольцо в К. .
. = 5Z = { 5k / k
= 5Z = { 5k / k  )|a, b, d
)|a, b, d 

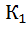 ={ (
={ (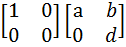 =
=  а не = 0
а не = 0 идеал а
идеал а 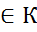 ; а +
; а +  }. Пусть это левый смежный класс элемента а. <К +>- аддетю коммут. Группа. Если
}. Пусть это левый смежный класс элемента а. <К +>- аддетю коммут. Группа. Если  , +> комутат. группа
, +> комутат. группа <| K адд.
<| K адд.  k
k 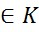 ;
; 



