
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение положения двух пунктов по двум исходнымСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте (задача Ганзена)
Практически это есть задача по определению двойной прямой засечкой двух пунктов по двум исходным. Координаты двух точек Р и Q могут быть определены, если в точках Т1 и Т2 измерить углы φ1,φ2,ψ1,ψ2 образуемые направлениями на два определяемых пункта P и Q (рис. 22). Однако точки Т1 и Т2 недоступны для измерений, а углы φ1,φ2,ψ1,ψ2 неизвестны. Для аналитического определения данных углов, на местности измеряют углы β1,β2,β3,β4 . Существует много способов решения этой задачи. Наиболее простым из них является способ условных координат, суть которого заключается в определении условных координат точек Т1 и Т2 в единой условной системе координат для всех точек (Т1,Т2,P,Q - в условной системе координат фигура останется подобной исходной). Через условные дирекционные углы направлений вычислить неизвестные углы φ1,φ2,ψ1,ψ2. Затем, перейдя в заданную систему координат, определить координаты искомых точек прямой однократной засечкой по формулам 43 и 44. Рассмотрим алгоритм решения задачи.
рис. 22 1. Зададим условную систему координат. Примем точку Р за начало условных координат x'Py', а направление PQ — за положительное направление оси ординат. Расстояние PQ условно примем равным, например, 10 000,000 м. Тогда условные координаты точек Р и Q будут:
x'p =0; y'p = 0; x'q =0; y'Q = 10 000, 000 м.
2. Определим условные дирекционные углы направлений Для решения прямой засечки в условных координатах, определим в условной системе координат дирекционные углы направлений: αРQ = 90º т.к. РQ задает ось ординат условной системы координат. Тогда условные дирекционные углы направлений можно вычислить через измеренные углы β1,β2,β3,β4,β5. Из рисунка 22 следует:
α'РТ1 = αРQ - β2 α'QТ1 = αРQ – 180 + β3 α'РТ2 = α'РТ1 + β1 α'QТ2 = αРQ – 180 + β4
3. Используя формулы 43 и 44 в ычислим условные координаты точек Т1 и Т2 По формулам прямой засечки из треугольников PQТ1 и PQТ2 найдем соответственно условные координаты точек T1
4. Вычисление углов φ1,φ2,ψ1,ψ2 по условным координатам По условным координатам точек Т1 и T2 можно определить условный дирекционный угол (Т1Т2)' из решения обратной геодезической задачи, после чего отыскать все углы, образуемые направлениями с точек Т1 и Т2на точки Р и Q как разности дирекционных углов соответствующих направлений:
Аналогично находят углы φ2 и ψ2. В отыскании углов φ1,φ2,ψ1,ψ2 при точках Т1 и Т2 и состояла цель введения условных координат.
5. Вычисление истинных дирекционных углов с точек Т1 и Т2 на определяемые точки Р и Q По истинным координатам точек Т1 и T2 определим дирекционный угол (Т1Т2) из решения обратной геодезической задачи, после чего вычислим все дирекционные углы, образуемые направлениями с точек Т1 и Т2на точки Р и Q:
6. Вычисление истинных координат определяемых точек Р и Q По действительным координатам точек Т1 и Т2 найдем искомые координаты точки Р из треугольника Т1Т2Р:
Координаты точки Q можно найти из треугольника T1T2Q
При таком определении координат точек Р и Q возможные промахи в измерениях или в выписке исходных данных обнаружены не будут. Поэтому с целью проверки правильности определения координат точек Р и Q по крайней мере на одной из них должно быть измерено добавочное направление на третий исходный пункт Т3 и дважды определен дирекционный угол (QT3)
где
Точность определения координат искомой пары точек зависит главным образом от величины углов четырехугольника, образованного двумя данными и двумя искомыми точками. Наибольшая точность получается тогда, когда образованный четырехугольник по своей форме близок к квадрату.
При выполнении привязки данным способом, необходимо делать абрис, на котором нужно указать, как измерялись углы. Пример решения задачи Ганзена.
Исходные данные Пункт x y T1 5186.006 5320.088 T2 3104.924 7302.548 T3 2292.775 7830.615
N/N betta b1 255°16' 33" b2 323°17' 19" b3 43°14' 15" b4 100°52' 16" b5 134°24' 45" 1. Определение координат п. Т’1 и Т’2 в условной системе координат Путкт Т1 Пункт Т2 из треугольника Т1Р1Р2 и треугольника Т2Р2P1:
X’p1 = 0.000 X’p2 = 0.000 Y’p1 = 0.000 Y’p2 = 10000.000 α’P1Т1 = 345° 16'33.0" α’P1Т2 = 53° 17'19.0" α’P2Т1 = 313° 14'15.0" α’P2Т2 = 10° 52'16.0"
2. Вычисление условного дирекционного угла α’T1Т2 и искомых углов φ1, φ2, φ3, φ4, (Искомые углы находят как разность соответствующих дирекционных углов.)
α’T1Т2 = 104°12'26.3" φ1 = 32° 2'18.0" φ2 = 29° 1'48.7" φ3 = 50°55' 7.3" φ4 = 42°25' 3.0" 3. Вычисление истинных координат точек Р1 и Р2. Для этого необходимо определить истинный дирекционнй угол направления Т1Т2 - αT1Т2 и истинные дирекционные углы направлений Т1Р1, Т1Р2, Т2Р1 и Т2Р2.
Из треугольника Т1Р1T2: И из треугольника Т2Р2T1:
XT1 = 5186.006 XT2 = 3104.924 YT1 = 5320.088 YT2 = 7302.548 αT1P1 = 197°27'31.7" αT1P2 = 165°25'13.7" αT2P1 = 265°28'17.7" αT2P2 = 223° 3'14.7"
4. Контроль вычислений.
Контролем вычислений служит вычисление угла β5 через разность дирекционных углов направлений Р2Р1 и Р2Т3. А) определение дирекционного угла αР2Р1
αР2Р1 = 302º 10' 58.8" б) определение дирекционного угла αР2Т3
αР2T3 = 76º 35' 47.3" в) вычисление β5 β5 выч = αР2T3 + 360º - αР2Р1= 134º 24’ 48.5” β5 изм = 134°24' 45" Разность измеренного и вычисленного угла составила 3.5”, что соответствует точности измерений угла полигонометрии IV класса.
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 1293; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.106 (0.008 с.) |


 и T2
и T2  :
: (137)
(137) (138)
(138)
 º.
º.




 .
.
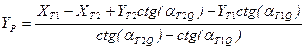 .
. (139),
(139),
 (140).
(140).





