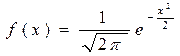Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Стандартизации и сертификации»Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
УЧЕБНОЕ ПОСОБИЕ по дисциплине «Основные понятия метрологии, Стандартизации и сертификации» (для специальности 270118 (550118) – «Искусственные сооружения на транспорте, способы их возведения и эксплуатации»)
Москва 2008 УДК 006.9 ББК 30.10
Васильев А. И. Основные понятия метрологии, стандартизации и сертификации: Учебное пособие. – М.: МАДИ. – 64с.
Рецензент: канд. техн. наук В. М. Фридкин
Учебное пособие по дисциплине «Метрология, стандартизация и сертификация» включает разделы, содержащие основные понятия метрологии, стандартизации и сертификации. Учебное пособие содержит основы теории погрешностей, способы выявления и устранения систематических, случайных и грубых погрешностей. В пособии приводится описание основных измерительных приборов, применяемых в транспортном строительстве, принципы работы компьютерных измерительных систем. Даются содержание и методы контроля качества строительной продукции. Пособие предназначено для студентов специальности 270118(550118) «Искусственные сооружения на транспорте, способы их возведения и эксплуатации».
© Московский автомобильно-дорожный институт (государственный технический университет),2008 Предисловие Решение транспортной проблемы в нашей стране во многом зависит от качества строительства и эксплуатации сооружений транспорта. Эффективный контроль качества строительной продукции невозможен без надежного метрологического обеспечения всех строительных и эксплуатационных процедур. Поэтому знание студентами принципиальных положений и основных методик инженерной метрологии является важной составляющей их квалификации как специалистов. Настоящее учебное пособие объясняет основные понятия метрологии, стандартизации и сертификации, содержит сведения по системам измерений, прежде всего – системам СИ и метрической, а также элементы теории погрешностей, включая способы выявления и исключения погрешностей измерений на основе методов теории вероятностей и математической статистики. Изложенный теоретический материал подкреплен примерами, ориентированными на практику транспортного строительства. Описаны наиболее часто используемые современные средства измерений для исследования состояния искусственных сооружений. В учебном пособии изложены главные задачи стандартизации и сертификации, их единство и взаимосвязь на базе законов метрологии. 1. Основные определения и характеристики Понятия метрологии, стандартизации и сертификации тесно связаны между собой. Метрология – наука о методах и средствах измерений. Стандартизация – деятельность по установлению требований к продукции и производственным процессам, а также правил оценки качества производимых изделий. Сертификация – процедуры по оценке соответствия продукции определенным требованиям. Стандартизация и сертификация возможны только на основе единой системы измерений, законов метрологии. В совокупности эти понятия обеспечивают упорядоченность всей деятельности человеческого общества и являются базой для развития техники и технологии. Измерения Метрология – греческое слово, образованное от слов «метрон» - мера и «логос» - учение. По определению, содержащемуся в ГОСТ 16263 – 70 «ГСИ. Метрология. Термины и определения», метрология – наука об измерениях, методах и средствах обеспечения их единства, а также о способах достижения требуемой точности измерений. Само же понятие «измерения» имеет самый широкий смысл. Для всего живого измерения являются средством ориентации в пространстве и времени, что позволяет ему жить и развиваться. Способность к измерениям заложена на генетическом уровне, причем, чем более развит организм, тем более разнообразные и осмысленные формы эта способность приобретает. Например, семена растений и личинки насекомых чувствуют время и температуру, многие растения в зависимости от степени освещения раскрывают или сворачивают цветы и листья, подсолнух поворачивает свое соцветие вслед за солнцем и т. п. Животные могут оценивать расстояния и скорость своего и не только своего передвижения. На этой способности строится довольно сложная тактика охоты со стороны хищника и спасения – со стороны его жертвы. Наконец, человек, «Homo sapiens», придал измерениям сознательную цель, сделал их инструментом анализа и творчества, одним из главных способов взаимодействия с природой и в человеческом сообществе. В технике объектами измерений могут быть любые физические тела, явления, процессы. Каждый из них характеризуется рядом свойств, отражающих его сущность. Свойство, присущее многим физическим объектам в качественном, но индивидуальное для каждого объекта в количественном отношении, называется в метрологии физической величиной. Таким образом, мы можем дать следующее определение: Измерение – это нахождение значений физической величины опытным путем, как правило, с помощью специальных технических средств. Пример. Прочность и упругость – свойства, которыми обладают все материалы, но у всех разные величины и прочности, и упругости. Основные функции измерений: 1) Измерения – путь познания природы. Они качественно и количественно характеризуют материальный мир, раскрывая действующие в природе закономерности. Известный английский метролог Томсон писал: «Каждая вещь известна лишь в той степени, в какой ее можно измерить». Пример. Измерения характеристик погоды: - тепло - холодно, ясно - пасмурно – это качественные оценки, их также можно трактовать как элементарные количественные, состоящие из двух значений; - измерение температуры воздуха, воды, силы ветра – количественные оценки. 2) Измерения – основы научных знаний. По выражению великого русского ученого Д.И. Менделеева: «Наука начинается с тех пор, как начинаются измерения». Многие отрасли науки основаны, главным образом, на измерениях. К таковым, в частности, относятся экспериментальная физика, сопротивление материалов. 3) Измерения – инструмент управления техническими и социальными процессами. Примеры: - измерения температуры бетона позволяют управлять процессом его твердения; - измерения размеров изделий являются элементом управления качеством продукции; - социологические опросы помогают определять социальные потребности общества. 4) Измерения – философская категория. Поскольку любое материальное тело или процесс существует во времени и пространстве – положение их во времени и пространстве можно оценить только путем измерений. Любая система взглядов на мир, общество, человека как личность, строится на определенных сопоставлениях количественных и качественных характеристик различных объектов. Будем далее рассматривать измерения физических величин, относящихся, главным образом, к строительным сооружениям. Количественная оценка физической величины составляет существо процесса измерения. Эта оценка состоит в определении ее размера относительно однородной с ней физической величины фиксированного размера, которой присваивается численное значение, равное единице. Физические величины измеряют с помощью средств измерений, которые имеют свои меры. Средства измерений могут быть естественными (ступня, шаг, сутки, год и т.п.) и техническими (измерительные приборы). Мерой называется средство измерения, предназначенное для воспроизведения единичной физической величины. Одни и те же физические величины можно измерить различными средствами со своими мерами. Пример. Длину пролетного строения можно измерить следующими способами:
Чтобы сравнивать результаты измерений, полученные разными средствами, необходимо иметь единицы измерений, закрепленные в эталонах. Эталон – средство измерений, предназначенное только для воспроизводства и хранения данной единицы измерений. Примеры: - ранее за эталон 1м принималось расстояние, равное 10-7 от одной четверти меридиана Земли, проходящего через Париж. Теперь первичным эталоном стала длина волны оранжевой линии спектра криптона, точнее, длина 1650763,73 этих волн; - эталон 1кг массы – масса 0,001 м3 чистой воды при температуре 40 Со. Основные понятия теории погрешностей Целью измерений физической величины является максимально точная оценка ее истинного значения, идеально отражающего некоторое свойство данного объекта как в количественном, так и в качественном отношении. Однако любой результат измерения есть лишь приближенная оценка истинного значения физической величины. Погрешностью результата измерения называют разницу D= X-Q, (2.1) где Q – истинное значение физической величины; X – результат измерения физической величины. Погрешность результата измерения складывается из погрешности средства измерения, неадекватности методики измерений и несоответствия условий измерения и условий использования полученного результата. Пример. Погрешность лабораторных измерений прочности бетона путем испытания кубиков: - погрешность манометра на прессе; - приближенность определения значения прочности по трем кубикам; - несоответствие условий испытания бетонных кубиков и реальной работы бетона в конструкции. Классификация погрешностей 1) По характеру проявления: Случайная погрешность может оцениваться только вероятностными (статистическими) методами (например, при измерениях физико-механических характеристик строительных материалов). Систематическая погрешность – постоянная или закономерно меняющаяся при повторных измерениях (например, из-за неправильной тарировки средств измерения; отставание или слишком быстрый ход часов). Прогрессирующая погрешность (дрейфовая) – непредсказуемая погрешность, медленно меняющаяся во времени (например, при оценке развития трещин в бетоне или перспективных параметров автомобильного движения). Грубая погрешность – это случайная погрешность отдельного наблюдения (ошибка при считывании отсчета с прибора, резкое изменение условий и т.п.). 2) По способу выражения (точность измерения): Абсолютная погрешность D, выраженная в тех же единицах, что и измеряемая величина Q. Относительная погрешность D/ Q. Приведенная погрешность D/ QN, где QN - условно принятое значение Q на всем диапазоне наблюдения (обычно, верхний предел Q). 3) По причинам: Инструментальная – погрешность самого инструмента (например, точность измерения деформаций в конструкции тензометром – 1-2 мкм, точность хода часов – 1 с в сутки). Методическая погрешность, как правило, обусловлена: - отличием принятой для анализа модели измеряемой физической величины от ее истинного поведения (например, расчетная схема конструкций имеет ряд условностей, таких как идеальные шарниры в узлах, тогда как на самом деле узлы фермы являются жесткими соединениями, и т.п.); - влиянием способа измерения (например, при испытаниях частот колебаний часто не учитывается влияние массы временной нагрузки); - влиянием формул вычисления результатов (приближенность формул - например, условность величины модуля упругости и др.); - влиянием других неучтенных факторов. Субъективная погрешность – погрешность отсчета оператором (например, оценка показаний прибора в пределах цены деления). 4) По зависимости от значений измеряемой величины Аддитивная – не зависит от измеряемой величины (например, точность измерения длины рулеткой). Мультипликативная – изменяется линейно (высотные отметки при наклоне трубы нивелира). Нелинейная – находится в нелинейной зависимости от измеряемой величины (измерение температурных напряжений в статически неопределимых конструкциях). 5) По влиянию внешних условий Основная – погрешность, проявляющаяся в нормальных условиях (т.е. в оговоренных пределах) (температура, влажность, давление и т.п.). Дополнительная – возникающая из-за отклонения каких-либо факторов от нормативных пределов (резкое изменение температуры, неравномерный нагрев из-за солнечной радиации и т.п.). 6) По характеру изменения измеряемой физической величины Статическая – погрешность в условиях, когда измеряемая физическая величина постоянна; Динамическая – измеряемая физическая величина меняется, и реакция прибора не успевает за ее изменением (например, измерение колебаний балки в нескольких точках). Суммирование погрешностей В общем случае погрешность измерений образуется по совокупности причин и представляет собой результат суммирования нескольких ее составляющих. Правила суммирования погрешностей, составляющих результирующую погрешность, должны учитывать характер каждой из них и вероятность их сочетания. Практические правила суммирования состоят из следующих расчетных процедур. 1) Все суммируемые погрешности, так же как и результирующая, представляются как случайные величины. Суммирование заключается в определении параметров распределения результирующей погрешности. 2) Все суммируемые составляющие необходимо разделить на аддитивные и мультипликативные. 3) Для каждой составляющей погрешности следует вычислить параметры ее распределения: среднее значение и стандарт. Для мультипликативных погрешностей эти параметры определяются в начале и конце диапазона измерений. 4) Необходимо учесть корреляционные связи между составляющими погрешностями и по определенным критериям, выделить группы сильно коррелированных между собой погрешностей, для которых принять коэффициент корреляции – 1, а также группы слабо коррелированных погрешностей, в которых корреляцию не учитывать. 5) Для определения суммарной погрешности и параметров ее распределения при наличии мультипликативных погрешностей эти параметры вычисляют для начального и конечного значений измеряемой величины, а их промежуточные значения определяют по интерполяции. 6) Параметры распределения результирующей погрешности Z определяются по правилам суммирования случайных величин на начало и конец измерений по следующим формулам. Средняя величина (алгебраическая сумма):
.. (2.3)
Стандарт для слабо коррелированных между собой погрешностей:
где m – число суммируемых погрешностей.
Контрольные вопросы: 1. Дайте определение погрешности измерений. 2. Объясните различия погрешности по характеру их проявления. 3. Назовите возможные причины погрешностей измерения. 4. Назовите правила округления погрешностей. Приведите примеры. 5. Как суммируются сильно и слабо коррелированные составляющие погрешности? Систематические погрешности Систематическая погрешность представляет собой функцию влияния на результаты измерений определенных факторов, состав которых зависит от физических, конструктивных и технологических особенностей средств измерений, условий их применения, а также индивидуальных качеств наблюдателя. Пример. При измерении профиля проезжей части моста могут возникнуть систематические погрешности вследствие негоризонтальности трубы нивелира, неучета влияния солнечной радиации и т.п.
Случайные погрешности Случайная погрешность – это составляющая погрешности измерения, которая изменяется случайным образом в серии повторных измерений одного и того же размера физической величины, проведенных с одинаковой тщательностью в одних и тех же условиях. Случайные погрешности неизбежны, неустранимы и их можно описать и ограничить только приемами математической статистики. При этом необходимо решить две задачи: - установить закон распределения вероятностей случайной погрешности и убедиться, что массив измерений соответствует этому закону; - получить интервальную оценку истинного значения измеряемой физической величины. Применительно к исследованию свойств строительных материалов и конструкций можно утверждать, что в большинстве случаев случайные погрешности имеют вероятностную основу, подчиняющуюся нормальному закону распределения, который описывает случайные величины, зависящие от многих незначительных случайных факторов. Поэтому в настоящем курсе мы ограничимся рассмотрением именно этого распределения. Познакомиться с другими законами распределения читатель может в специальной литературе по теории вероятностей, математической статистики, теоретической метрологии. Итак, нормальным называется распределение вероятностей случайной величины х, подчиняющееся закону: плотность распределения:
функция распределения:
Математическое ожидание M(x) при этом равно α: среднеквадратическое отклонение (стандарт) – s. Как видно из приведенных формул, нормальное распределение симметрично относительно математического ожидания. Путем замены переменных t = (x-a) /s это распределение можно привести к нормированного виду, для которого M (t) =0 и s (t) =1, т.е.:
Для плотности и функции нормированного нормального распределения составлены таблицы (табл. 1 и 2 приложения). Грубые погрешности Грубая погрешность (промах) – это погрешность результата отдельного измерения, входящего в ряд измерений, который для данных условий резко отличается от остальных результатов. К наиболее распространенным причинам грубых погрешностей можно отнести: - неправильный отсчет по шкале измерительного прибора; - неправильная запись результата измерений; - резкое изменение условий измерения(например, изменение питающего прибор электрического напряжения). Основным способом недопущения грубых погрешностей являются повторные измерения. Для выявления и исключения грубых погрешностей применяются статистические методы. Механические приборы Для измерения перемещений, например, прогибов пролетных строений мостов или деформаций контура водопропускных труб и обделок тоннелей, обычно применяют прогибомеры часового типа. Эти приборы имеют цену деления 0,1 мм, просты в установке и считывании результатов. Наиболее известны прогибомеры Максимова, Аистова. Углы поворота элементов измеряют уровнями или инклинометрами. Напряжения в конструктивных элементах от приращения нагрузки непосредственно измерить невозможно. Для их оценки используется известный закон Гука: σ= Е ×ε, (6.1) где σ – напряжение (кгс/см2 или МПа); Е – модуль упругости материала в тех же единицах; ε - относительная деформация на базе измерения. Приборы для измерения напряжений – тензометры, устанавливаются на поверхность, на которой измеряются напряжения, на некоторой базе Б. Относительная деформация ε определяется отношением Таким образом, формула (6.1) может быть записана в виде:
, (6.2)
где Δ – отсчет по шкале тензометра; М – масштаб (передаточное число) тензометра (для механических рычажных тензометров, как правило, М ≈1000). База тензометра выбирается в зависимости от материала конструкции и ожидаемого напряжения. Для металла это, как правило, 20…100 мм, для бетона – 200…500 мм.
Электрические тензометры Тензорезисторы Действие такого датчика основано на преобразовании деформации в изменение электрического сопротивления. Преобразователем служит высокочувствительная спираль из специального сплава, например, константана, которая приклеивается к элементу конструкции, деформацию которого надо измерить. Высокая температурная зависимость показаний этого прибора требует обязательного наличия второго, компенсационного тензорезистора, находящегося в одинаковых с первым условиях, но не испытывающего деформаций за счет силового воздействия. Измерительные приборы на базе тензорезисторов требуют применения высококачественных аналоговых усилителей, хороших источников опорного напряжения и многоразрядных аналогово-цифровых преобразователей (АЦП). Этот традиционный подход отработан, но он имеет серьёзные недостатки. Главными из них являются проблемы, связанные с усилением очень слабого изменения сигнала тензодатчика и преобразованием его к цифровому виду: на результат накладываются всевозможные посторонние электромагнитные излучения, колебания температуры, нелинейность шкалы тензорезисторов и помехи, возникающие на плате в моменты переключения окружающих цифровых микросхем. Как правило, такие датчики используют только в лабораторных условиях.
Струнные тензометры Физическая сущность струнного тензометра заключается в том, что струна, прикрепляемая к конструкции, получает в результате деформации конструкции удлинение (укорочение) Δ L, отчего изменяется натяжение струны. Натяжение струны, в свою очередь, функционально связано с собственной частотой колебаний: N = где N – собственная частота колебаний струны; L – длина струны; σ – напряжение в струне; ρ – плотность материала струны. От приращения напряжения в струне можно перейти к приращению напряжения в конструкции, используя соотношение модулей упругости. Индуктивные тензодатчики Более широкое применение в полевых условиях находят индуктивные датчики малых перемещений. Они герметичны и имеют стабильный температурный коэффициент. Индуктивный датчик представляет собой дифференциальный дроссель с симметрично расположенными друг относительно друга обмотками индуктивности. Измерительный якорь, передвигающийся между обмотками, создает синфазное изменение их индуктивности, обеспечивая тем самым преобразование линейных перемещений якоря в электрическую величину. Электронные тензометры Оптоволоконные датчики Наиболее приспособленными к измерениям напряженно-деформированного состояния натурных конструкций в полевых условиях являются оптико-механические датчики. Примером такого прибора может служить датчик, созданный в научно-проектном институте исследования мостовых и других инженерных сооружений (Институт ИМИДИС). Основой этого оптоэлектронного линейного датчика перемещений является прибор с зарядовой связью, представляющий собой линейку фотоэлементов со схемами управления и считывания информации. Используемая линейка состоит из 2048 фотоэлементов, расположенных в одну линию. Размер каждого элемента 14х14 мкм. В процессе работы с микросхемы снимается напряжение в виде пачки из 2048 импульсов прямоугольной формы, амплитуда которых зависит от освещенности соответствующих фотоэлементов. В зависимости от величины деформации часть фотоэлементов закрывается специальной подвижной шторкой и соответственно меняется освещенность. Показания этого датчика практически не зависят от потерь напряжения в кабелях питания и связи.
Инклинометры и прогибомеры Инклинометры Инклинометры (датчики крена и угловых перемещений) с электрическим выходным сигналом, пропорциональным углу наклона датчика, являются сравнительно новыми приборами, доведенными до широкого промышленного применения в последние годы. По своему принципу действия инклинометр представляет собой дифференциальный емкостной преобразователь наклона, включающий в себя чувствительный электрический элемент в форме капсулы. Выходной сигнал датчика пропорционален величине емкости дифференциального конденсатора, которая линейно зависит от положения корпуса в вертикальной плоскости. Прогибомеры Оптоэлектронный доковый прогибомер был разработан для контроля деформаций плавающих доков в вертикальной плоскости в процессе их эксплуатации и постройки. Он может использоваться для измерения деформаций прогиба судов, находящихся под погрузкой и разгрузкой, деформаций мостов, плотин и других крупногабаритных конструкций, для контроля состояния нефтедобывающих платформ и нефтеналивных судов. Недостатки этого прогибомера: низкая точность и большие габариты, что не позволяет использовать его при испытании малых мостов. Эти недостатки в значительной степени устраняют разработанные в Институте ИМИДИС рычажные и колесные оптоэлектронные прогибомеры, предназначенные как для статических, так и для динамических испытаний мостов и других строительных конструкций. Рычажный прогибомер имеет рычаг переменной длины для регулирования чувствительности и диапазона измерений. При стандартной длине рычага – 12 см прогибомер имеет точность измерения 0,1 мм в диапазоне ±50 мм. Колесный прогибомер при такой же точности имеет неограниченный диапазон измерений.
Назначение сертификации Сертификация представляет собой действие, удостоверяющее посредством сертификата соответствия или знака соответствия, что изделие или услуга соответствует определенным стандартам или другому нормативному документу. Область сертификации весьма широкая: - обязательная сертификация требуется, когда речь идет о безопасности и здоровье; - добровольная сертификация полезна для подтверждения квалификации производителя продукции. Сертификацию проводят независимые организации по определенным правилам. В международном плане широко применяется комплект документов ИСО-9000 по управлению качеством продукции. Его примерная схема (рис.7.2):
Рис.7.2. Схема управления качеством продукции по системе ИСО – 9000
Сертификация по системе ИСО – 9000 трудное, но весьма перспективное мероприятие. Оно помогает реально улучшить организацию труда, систему управления качеством продукции и является в определенной степени характеристикой квалификации предприятия.
Е) другие виды контроля Кроме качества строительно-монтажных работ в функции технического надзора также входят: - контроль за объемами выполнения строительно-монтажных работ; - контроль затрат (по заданию Заказчика); - контроль за осуществлением мероприятий по охране труда и технике безопасности; - контроль за соблюдением экологических требований; - контроль за мерами по обеспечению безопасности движения транспортных средств и пешеходов в местах производства работ.
Заключительным этапом контроля в процессе строительства сооружения являются приемочные обследования и испытания, которые проводятся с целью установить степень соответствия работы сооружения под нагрузкой проектным предпосылкам и возможность приемки его в эксплуатацию. Во время эксплуатации контроль качества принимает форму регулярных осмотров и обследований с целью уточнения режима содержания сооружения.
Контрольные вопросы: 1. Покажите взаимосвязь метрологии, стандартизации и сертификации. 2. Перечислите виды нормативных документов. 3. Какие процедуры включает в себя технический надзор? 4. Какие виды контроля качества применяют на строительной площадке? ПРИЛОЖЕНИЕ Таблица 1 Значения функции
Таблица 2 Значения функции Лапласа
|
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 409; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.16.40 (0.013 с.) |

 . (2.2)
. (2.2)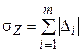 Стандарт для сильно коррелированных между собой погрешностей:
Стандарт для сильно коррелированных между собой погрешностей: , (2.4)
, (2.4) ; (4.1)
; (4.1) . (4.2)
. (4.2) ; (4.1’)
; (4.1’) - (функция Лапласа). (4.2’)
- (функция Лапласа). (4.2’)
 , где Δ Б - изменение базы при загружении элемента дополнительной нагрузкой.
, где Δ Б - изменение базы при загружении элемента дополнительной нагрузкой.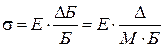
 , (6.3)
, (6.3)