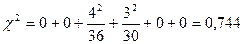Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценка близости распределения результатов измерений теоретическому законуСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для такого роста оценки используются так называемые критерии согласия. Разными учеными предложен целый ряд критериев согласия. На практике наиболее распространен критерий Пирсона. Суть критерия Пирсона состоит в сравнении гистограмм результатов измерений и соответствующих значений по теоретическому распределению. При этом число измерений желательно иметь не менее 50. Сравнение производится путем вычисления величины c2:
где ni, Ni – экспериментальные и теоретические значения частот в i –ом интервале гистограммы; m – число интервалов в гистограмме; Pi – значение вероятности попадания в i – й интервал в теоретическом распределении;
При достаточно большом n случайная величина c2 подчиняется распределению Пирсона (распределению c2) с числом степеней свободы ν =m-1-r, где r – необходимое число параметров теоретического распределения, которые совпадают с полученными по результатам измерений: для нормального распределения r = 2 (параметры – математическое ожидание и среднее квадратическое отклонение), т.е. ν = m-3. Полученные значения c2 сравниваются с их критическими значениями (c2кр), которые определены применительно к разным уровням значимости q (приложение, табл.5). Уровень значимости определяет вероятность ошибки, если гипотеза о правильном подборе теоретического распределения отвергается. При условии c2£ c2кр, при заданном значении q гипотеза о совпадении экспериментального и теоретического распределений принимается. Пример: Пусть имеется 100 результатов измерения прочности R бетона в МПа: Rj: 30 31 32 33 34 35 36 37 38 39 40 nj: 1 3 7 12 15 25 18 9 5 4 1. Определить, соответствует ли полученный массив данных нормальному распределению.
Построим гистограмму экспериментальных данных с интервалом 2 МПа от 29,5 МПа до 41,5 МПа (рис. 4.1). Рис. 4.1. Гистограмма результатов измерения и теоретического распределения Для построения гистограммы теоретического распределения определим его математическое ожидание и среднее квадратическое отклонение:
Используя таблицу значений функции Лапласа, находим в соответствующих интервалах теоретические частоты. Интервал: 29.5 – 31.5 ® Р1 =0,497 – 0,460=0,037; N1 =0,037×100» 4; 31.5 – 33.5 ® Р2 =0,460 – 0,273=0,187; N2 =19;
33.5 – 35.5 ® Р3 =0,273 + 0,099=0,364; N3 =36; 35.5 – 37.5 ® Р4 =0,394 – 0,099=0,295; N4 =30; 37.5 – 39.5 ® Р5 =0,488 – 0,394=0,094; N5 =9; 39.5 – 41.5 ® Р6 =0,499 – 0,488=0,011; N6 =1.
Вычислим далее значение c2 и сравним его с критическими значениями для разных уровней надежности. Число степеней свободы в данном случае равно ν =6-3=3. Для q = 0,80 имеем c2кр = 1,05 (табл. 4 приложения); для q = 0,90 – c2кр = 0,63. Таким образом, можно говорить о правильности гипотезы, что массив результатов соответствует теоретическому нормальному распределению c вероятностью 0,8, но нельзя это утверждать с вероятностью 0,9.
|
|||||||||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 546; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.90.244 (0.007 с.) |

 , (4.3)
, (4.3)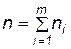 - число результатов измерений.
- число результатов измерений.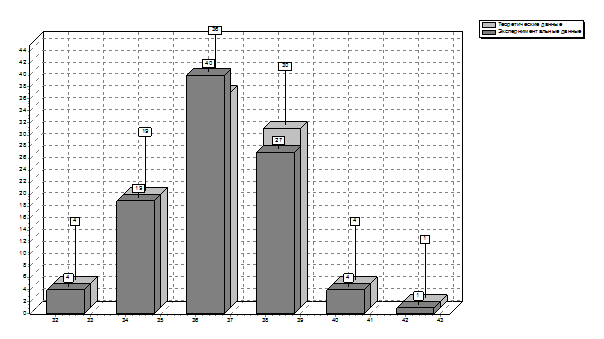
 МПа;
МПа; ; s(R) = 2,0 МПа.
; s(R) = 2,0 МПа.