
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Распределение частиц по размерамСодержание книги Поиск на нашем сайте
Частотой fi наблюдения случайной переменной x (например, размера частиц) в интервале значений D xi от xi до xi +1 называется отношение числа Ni наблюдений х в этом интервале к общему числу наблюдений х: fi = Ni / N. Зависимость fi от х называется эмпирическим распределением х. Его характеризуют: · средним арифметическим (или просто средним)` х:
· средним квадратичным отклонением (от среднего) s:
· коэффициентом вариации Плотностью вероятности (или функцией плотности вероятности) случайной переменной х называется функция f (x) такая, что:
Она имеет свойство, что её интеграл в пределах значений случайной переменной от x 1 до x 2 равен вероятности наблюдения х в этом интервале:
Функцию f (x) называют теоретическим распределением. К нему стремится эмпирическое распределение при N ® ¥ и D xi ® 0. Его характеризуют: · математическим ожиданием (или средним теоретического распределения):
· стандартным отклонением s:
· коэффициентом вариации V = m / s и другими параметрами.
Кумулятивной вероятностью Р (х ' £ x) величины х называют вероятность наблюдения х ' £ x. Она даётся интегральной функцией:
Многим эмпирическим распределениям приблизительно соответствует теоретическое распределение, называемое распределением Гаусса или нормальным распределением:
Кумулятивная вероятность переменной х, распределённой по этому закону, находится из интеграла стандартной (или единичной) функции Гаусса F (z):
 , ,
где z – аргумент стандартной функции Гаусса: z = (х – m)/ s. Численные значения интеграла стандартной функции Гаусса (интеграла вероятности) даются в таблицах математических справочников, учебников по теории вероятности и математической статистики, а также в виде графиков (см. рис. 1). Кроме того, они могут быть получены в математических приложениях для компьютера. (В Excel, в русской версии, F (z) вызывается кодом =НОРМСТРАСП(z)).
Адгезия наночастиц
По теории Дронсона-Кендела-Робертса, сила F притяжения (адгезии) шарообразной частицы одной фазы и бесконечной по протяженности плоской поверхностью другой или той же фазы выражается формулой
где А – константа Гамакера для данной системы (константа дисперсионного взаимодействия молекул фаз), r – радиус частицы, h – расстояние между поверхностью сферической частицы и плоской поверхностью.
Устойчивость нанодисперсных систем
Потенциальная энергия взаимодействия двух бесконечно больших плоских пластин (в расчете на единицу площади):
Первый член отвечает энергии электростатического отталкивания, второй член – энергии притяжения из-за дисперсионных (межмолекулярных) взаимодействий. A * – константа Гамакера, h – расстояние между поверхностями пластин, e r – относительная диэлектрическая проницаемость среды между пластинами, e 0 – электрическая постоянная (диэлектрическая проницаемость вакуума), p – число пи, j d – потенциал на границе диффузной части и плотной части двойного электрического слоя, величина i (каппа, параметр Дебая) равна обратной величине толщины диффузного слоя d:
F – постоянная Фарадея. Потенциальная энергия взаимодействия двух шарообразных частиц с одинаковыми радиусами r:
Аналогичная формула для двух шарообразных частиц с одинаковыми малыми радиусами r (r < 30 нм):
Электрокинетические свойства наночастиц
Электрофоретической подвижностью u частицы называется отношение скорости v движения частицы к напряженности электрического поля Е, вызывающего это движение, u = v / E. (Напряженность электрического поля равна градиенту электрического потенциала со знаком минус, а в случае однородного поля – отношению разности потенциалов электродов к расстоянию между ними.) Зависимость толщины ДЭС от ионной силы раствора: i –1 = (смысл обозначений см. в предыдущей теме). Связь между электрофоретической подвижностью u сферических частиц и дзета-потенциалом z (уравнение Генри):
где f (ia) – функция произведения радиуса частицы a и параметра Дебая i (каппа, обратная величина толщины диффузного слоя). Функция меняется от 1 при ia << 1 до 3/2 при ia >> 1. Пределу ia << 1 (малые частицы и большая толщина ДЭС) отвечает уравнение Хюккеля: u = Пределу ia >> 1 (большие частицы и малая толщина ДЭС) отвечает уравнение Гельмгольца-Смолуховского: u = Во всем интервале ia функция f (ia) выражается бесконечным рядом. Для шарообразных частиц она передается аппроксимирующей формулой Охсима (1994):
Потенциал течения под давлением р через капилляр радиусом r, намного превышающем толщину диффузного слоя внутренней поверхности капилляра: E теч k - удельная электрическая проводимость раствора, k ПВ – удельная поверхностная проводимость капилляра. Скорость течения (линейная скорость электроосмоса) при заданной напряженности поля E: v Объёмная скорость электроосмоса (объём раствора электролита, протекающий через трубку или систему капилляров за единицу времени при заданной разности потенциалов):
где I – измеренная сила электрического тока, k – удельная электрическая проводимость раствора. Примечание: в старых учебниках эти уравнения даются в системе СГС. В системах СИ и СГС они отличаются множителем 4p e 0.
Диффузия и броуновское движение наночастиц
Зависимость среднего квадрата сдвига при Броуновском движении от времени (уравнение Эйнштейна-Смолуховского):
D – коэффициент диффузии, t – время наблюдения. Аналогичная зависимость для среднего квадратичного сдвига (х скв):
Коэффициент диффузии частиц в вязкой среде (уравнение Эйнштейна):
D = k B T / f
f – коэффициент вязкого трения (вязкого сопротивления среды). Коэффициент вязкого трения сферической частицы с радиусом r (формула Стокса) в непрерывной среде с вязкостью h:
f = 6p hr
Коэффициент диффузии (или самодиффузии) сферической частицы (уравнение Стокса-Эйнштейна):
Приложение 2. Примеры решения задач
Пример 1. (Тема: распределение частиц по размерам) В образце наночастиц кремния Si найдено приблизительно нормальное распределение по размерам, со средним диаметром` х = 8.0 нм и со стандартным отклонением s = 1.9 нм. Определить долю числа частиц, диаметры которых больше 10 нм. Решение. Вычислим аргумент z стандартной функции Гаусса, приняв m =` х = 8.0 нм и s = 1.9 нм: z = (x – m)/ s = (10 нм – 8.0 нм)/(1.9 нм) = 1.05. По графику стандартной кумулятивной вероятности (рис. 1 в приложении 1) найдем F (1.05) = 0.85. Это – доля частиц, диаметр которых меньше или равен 10 нм. Так как доля частиц во всем диапазоне диаметров равна 1, то доля частиц с диаметрами больше 10 нм равна 1 – F (1.05) = 1 – 0.85 = 0.15.
Пример 2. (Тема: устойчивость нанодисперсных систем) Рассчитать энергию взаимодействия пары сферических частиц гидрозоля серебра с одинаковыми радиусами 32 нм, находящихся на расстоянии между их поверхностями h = 10 нм по следующим данным: константа Гамакера A * = 1·10–19 Дж, параметр Дебая i = 1·108 м–1, jd = 40 мВ, относительная диэлектрическая проницаемость e r = 80. Решение. Потенциальная энергия взаимодействия двух шарообразных частиц равна:
= 1.2·10–19 Дж.
Пример 3. (Тема: электрокинетические свойства наночастиц) Вычислить дзета-потенциал полистирольного латекса с радиусом монодисперсных частиц 61.0 нм, для которых обнаружена электрофоретическая подвижность 3.04·10–8 м2/(В·с) при 23 °С в водной среде с ионной силой 0.01 моль/л, вязкостью 0.894 мПа·с и относительной диэлектрической проницаемостью 78.5. Решение. Ответ следует из уравнения Генри. Чтобы воспользоваться им, вычислим сначала параметр ia: ia = (Ионная сила здесь переведена в СИ, 0.01 моль/л = 0.01 моль/0.001 м3 = 10 моль/м3). Затем вычислим функцию Генри по формуле Охсима:
В заключение, вычисляем по уравнению Генри:
Приложение 3. Единицы физических величин
Физическая величина – это произведение численного значения (числа) и единицы измерения. В СИ (официальное название: Le Système International d'Unités) определены семь основных единиц измерения и две дополнительные (таблица 1.1). Все остальные физические величины выводятся из основных с помощью умножения или деления в соответствии с физическими законами (формулами). Например, линейная скорость движения определяется уравнением v = dl/d t. Она имеет размерность (длина/время) и единицу измерения СИ (производную от основных единиц СИ) м/с. Некоторые из производных единиц имеют собственные наименования и обозначения (таблица 1.2). Для удобного обращения с большими или малыми численными значениями, в СИ применяются стандартные десятичные приставки, определяющие кратные и дольные десятичные производные. (Наиболее употребимые из них перечислены в табл. 1.3). Например, 1 нанометр (обозначается 1 нм) означает 10–9 долю метра, то есть 1 нм = 10–9 м. 1 миллипаскаль (1 мПа) означает 10–3 паскаля. Основная единица массы “килограмм” уже имеет приставку кило-. В этом случае любые другие десятичные производные образуются от десятичной производной “грамм”. Например, 1 миллиграмм, 1 мг, означает 10–3 г или 10–6 кг. (Грамм является основной единицей массы в СГС и десятичной дольной единицей СИ). Если над единицей измерения с десятичной приставкой производится математическое действие, например возведение в степень, то действие относится ко всему обозначению. Например, 1 дм3 означает 1 (дм)3, но не 1 д(м)3.
Таблица 1.1 Основные и дополнительные единицы СИ
* определение СИ: " Моль – это количество вещества, в котором содержится столько названных единиц, сколько содержится атомов в 0.012 кг изотопа 12С. " Можно сказать иначе, моль – это количество вещества, в котором содержится N A (число Авогадро) единиц вещества, которые должны быть ясно указаны. Например, в качестве единиц вещества могут рассматриваться формульные единицы AlCl3, 1/3AlCl3, ионы, электроны, мицеллы, частицы лиофобного золя, аэрозоля, эмульсии и т.д.
Табл. 1.2 Некоторые производные единицы СИ, имеющие собственные наименования
Таблица 1.3 Некоторые десятичные (дольные и кратные) приставки к единицам СИ
Согласно грамматическим правилам СИ, обозначение десятичной приставки и обозначение исходной единицы пишутся слитно и не сопровождаются точкой как указанием на сокращение наименования, однако знак пунктуации должен стоять, если этого требуют грамматические правила текста, в котором обозначение встречается. Например, если обозначение сантиметра, см, стоит в конце предложения, то точка должна стоять как обычно, см. Произведение двух разных единиц может быть записано тремя следующими способами (на примере вязкости): Па×с, Па·с, Па с (с пробелом между множителями). Отношение двух единиц может быть записано либо через дробь (например, Н/м), либо как произведение тремя способами: Н×м–1, Н·м–1 и Н м–1. Отношение трёх и более единиц измерения должно записываться в соответствии с обычными правилами математики (не допускается применение трёхэтажных дробей, знаменатель должен быть ясно определён, при необходимости с применением скобок). СИ является рекомендуемой и наиболее удобной системой единиц в теоретических вычислениях и в коммуникациях (передаче информации) в области точных наук. Однако во многих частных случаях удобным оказывается использование других единиц измерения. Например, при экспериментальных исследованиях с использованием высоких давлений удобно применять единицу измерения “бар”, а при использовании вакуума – “миллиметр ртутного столба” (аналогично тому, как при исчислении возраста человека используются не секунды или гигасекунды, а годы, тогда как для аналогичных целей в социальной истории применяются столетия). По определениям СИ, некоторые из таких единиц допускаются для “временного” применения, и применяются фактически (см. таблицу 1.4). Многие единицы из прошлой практики не рекомендованы к применению и, фактически, почти не применяются в современных измерениях, однако их так же полезно знать, так как многие источники информации (энциклопедии, справочники, другие публикации) используют их. Например, в большинстве справочных изданий по физической химии вязкость жидкостей указывается в сантипуазах, а не в единицах СИ Па·с. Важнейшие из таких единиц перечислены в табл. 1.5.
Табл. 1.4 Единицы измерения не входящие в СИ, но используемые наряду с единицам СИ
Табл. 1.5 Некоторые единицы измерения, применявшиеся в физической химии в прошлой практике, и не входящие в СИ
Приложение 4. Физические константы
* другое наименование этой константы – электрическая постоянная ** наименование "дальтон" не соответствует СИ, но оно часто применяется в химии полимеров и биохимии
Варианты контрольных заданий
Теоретические вопросы
Задачи
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 357; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.157.7 (0.015 с.) |

 ,
,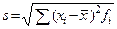 ,
, , и другими параметрами.
, и другими параметрами. .
. .
. ,
, .
.
 .
. или
или  ,
, ,
, .
.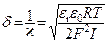 ,
,  – ионная сила раствора,
– ионная сила раствора, .
.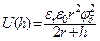 .
. .
.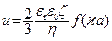 ,
, .
. .
. .
.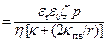 ,
,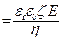 .
. ,
,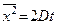

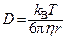

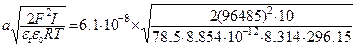 =20.12.
=20.12. = 1.35.
= 1.35. = 0.0434 В = 43.4 мВ.
= 0.0434 В = 43.4 мВ.


