
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
F- критерий для проверки качества оцениванияСодержание книги
Поиск на нашем сайте Даже если между Y и X отсутствует зависимость, по любой данной выборка наблюдений может показаться, что такая зависимость существует, возможно и слабая. Только по случайному стечению обстоятельств коэффициент корреляции и R2 будут в точности равны нулю. Итак, как узнать, действительно ли полученное для регрессии значение R2 отражает истинную зависимость или оно появилось случайно? В принципе, мы могли бы принять следующую процедуру. Предположим что регрессионная модель задается уравнением
Примем в качестве нулевой гипотезы, что связь между Y и X отсутствует, т.е H0: β2 = 0. Найдем значение, которое может быть превышено величиной R2 в 5% случаев. Затем используем эту цифру в качестве критического уровня R2 для проверки гипотезы при 5%-ном уровне значимости. Если этот уровень превышается, то мы отклоняем нулевую гипотезу в пользу H1: β 2 ≠ 0. Такая проверка, подобно t-тесту для коэффициента регрессии, не служит доказательством. Действительно, при 5%-ном уровне значимости имеется риск допущения ошибки I рода (отклонения нулевой гипотезы, когда она истинна) в 5% случаев, но можно, конечно, снизить этот риск за счет использования более высокого уровня значимости, например, равного 1%. Тогда критический уровень может быть превышен случайно только в 1% случаев, поэтому он выше критического уровня для проверки при 5%-ном уровне значимости. Каким образом можно определить критический уровень для R2 при любом уровне значимости? Здесь возникает небольшая проблема. У нас нет таблицы критических уровней для R2. Традиционная процедура состоит в использовании косвенного подхода и выполнения так называемого F-теста, основанного на анализе дисперсии. Предположим, что, как и ранее, вы можете разложить дисперсию зависимой переменной на «объясненную» и «необъясненную» составляющие, используя уравнение (1.46)
(Напомним, что е равняется нулю и выборочное среднее значение Y равняется выборочному среднему значению Y.) Левая часть здесь является обшей суммой квадратов (TSS) отклонений зависимой переменной от ее выборочного среднего значения. Первый член в правой части является объясненной суммой квадратов (ESS), а второй член — необъясненной (остаточной) суммой квадратов (RSS):
TSS=ESS + RSS. (2.85)
F-статистика для проверки общего качества регрессии записывается как отношение объясненной суммы квадратов в расчете на одну независимую переменную, деленное на остаточную сумму квадратов в расчете на одну степень свободы:
где к — число оцениваемых параметров в уравнении регрессии (к - 1 — коэффициенты наклона). После деления числителя и знаменателя отношения на TSS эта F-статистика может быть эквивалентно выражена на основе коэффициента R2:
В данном контексте к = 2, и, таким образом, уравнение (2.87) принимает вид
После вычисления F-критерия по значению коэффициента R2 вы отыскиваете величину Fкрит — критический уровень F в соответствующей таблице. Если F > Fкрит то вы отклоняете нулевую гипотезу и делаете вывод о том, что имеющееся «объяснение» поведения величины Y лучше, чем можно было бы получить чисто случайно. В табл. А.З представлены критические уровни для F при уровнях значимости 5 и 1 %. В каждом случае критический уровень зависит от числа независимых переменных (к - 1), которое находится в верхней строке таблицы, и от числа степеней свободы (п - к), которое находится в крайнем левом ее столбце. В данном контексте рассматривается случай парной регрессии, когда к = 2, и мы должны использовать первую колонку таблицы. В примере с функцией заработка из табл. 2.6, коэффициент R2 составил 0,1725. Поскольку было 540 наблюдений, F-статистика равняется R2 / [(1 - R2) / 538] = 0,1725 / (0,8275 / 538) = 112,15. При уровне значимости 0,1% критическое значение величины F при 1 и 500 степенях свободы (см. табл. А.З первый столбец, строка 500) составляет 10,96. Критическое значение при 1 и 538 степенях свободы еще меньше, и поэтому можно без колебаний отвергнуть нулевую гипотезу в нашем конкретном примере. Другими словами, лежащая здесь в основе величина R2 столь высока, что мы отклоняем предположение о том, что она могла появиться случайно. На практике F-статистика всегда вычисляется вместе с величиной R2, поэтому нет необходимости использовать уравнение (2.86). Почему же используется этот косвенный подход? Почему бы не иметь таблицу значений коэффициента R2? Ответ заключается в том, что таблица значений F-критерия является полезной для многих видов проверки дисперсии, одним из которых является расчет коэффициента R2. Вместо специализированной таблицы для каждого конкретного случая намного удобнее (или, по меньшей мере, экономнее) иметь одну обобщенную таблицу, делая при необходимости преобразования типа (2.86). Конечно, при необходимости можно вывести и критические значения коэффициента R2. Критическое значение R2 связано с критическим значением для F следующим уравнением:
из которого следует, что
В примере с функцией заработка критическое значение для F приуровне: значимости 1% составило примерно 10,95. Следовательно, в этом случае при к = 2
Хотя наша величина R2 и невелика, она превышает 0,020. Поэтому непосредственное сравнение величины R2 с его критическим значением подтверждает вывод о том, что в результате.F-теста мы должны отклонить нулевую гипотезу.
|
||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 488; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.009 с.) |

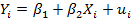 (2.8)
(2.8)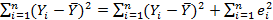 (2.84)
(2.84)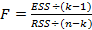 (2.86)
(2.86)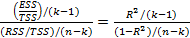 (2.87)
(2.87)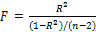 (2.88)
(2.88)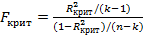 (2.89)
(2.89) (2.89)
(2.89)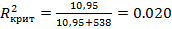 (2.91)
(2.91)


