
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тест Чоу на неудачу предсказанияСодержание книги
Поиск на нашем сайте
Как мы видели в предыдущем подразделе, ошибку предсказания можно рассчитать, добавив набор фиктивных переменных для наблюдений периода предсказания. Теперь вполне естественно определить, существенно ли ошибка предсказания отличается от нуля, и мы можем сделать это с помощью F-теста на совместную объясняющую способность фиктивных переменных. Совместив период выборки и период предсказания, мы оценим уравнение регрессии сначала без набора фиктивных переменных, а затем — вместе с ним. Обозначим полученные суммы квадратов отклонений как RSST+p и RSSD T+p; где нижний индекс показывает число наблюдений в регрессии, а верхний индекс D означает включение в уравнение фиктивных переменных. С помощью F-теста описанного в разделе 3.5, мы можем определить, было ли существенным улучшение качества уравнения после добавления набора фиктивных переменных. Улучшение равно (RSST+ р – RSSD T+p); число фиктивных переменных — P; сумма квадратов отклонений после включения фиктивных переменных — RSSD T+p; остающееся число степеней свободы равно числу наблюдений в совмещенной выборке (T+Р) за вычетом числа оцененных параметров (k + Р). В итоге значение F-статистики составит:
На самом деле для реализации теста даже не требуется оценивать уравнение регрессии с фиктивными переменными, поскольку значение RSSD T+p равно значению RSST— сумме квадратов отклонений для уравнения регрессии, оцененного на периоде выборки. Качество этой регрессии в точности такое же, как и у регрессии для первых Т наблюдений в уравнении с фиктивными переменными, и отклонения здесь те же самые. Для последних Р наблюдений в уравнении с фиктивными переменными нет отклонений, так как включение специальной фиктивной переменной для каждого наблюдения гарантирует точность уравнения для этих наблюдений. В итоге значение RSSD T+p в точности такое же, как и значение RSST, и F-статистика может быть переписана как
Этот тест известен как тест Чоу на неудачу предсказания и был назван так по имени своего создателя (Chow, 1960), однако приводимая здесь интерпретация теста была предложена несколько позже X. Песараном, Р. Смитом и С. Ео (Pesaran, Smith, Yeo, 1985). Пример Функция расходов на жилье вначале была оценена для периода 1959— 1999 гг., со значением RSST= 0,009673, а затем — для периода 1959—2003 гг., при этом RSST+p = 0,011937. Следовательно, F-статистика равна
Нулевая гипотеза заключается в том, что все коэффициенты при фиктивных переменных равны нулю. Критическое значение F(4; 38) на 5%-ном уровне значимости составляет 2,62. Следовательно, различие между качеством уравнения для периода оценивания и периода предсказания отсутствует, и мы не отвергаем гипотезу об устойчивости модели. F-тест на устойчивость коэффициентов Если для периода предсказания имеется достаточное число наблюдений, т.е. можно проверить, совпадали ли значения коэффициентов в период выборки и период предсказания, выполнив тест Чоу так, как это описано в гл. 5. Чтобы выполнить этот тест, нужно оценить отдельные регрессии для периода выборки и периода предсказания, а затем для всего периода и проверить, дает ли разбиение всего периода на периоды выборки и предсказания значимое улучшение оценок по сравнению с оценками для всего периода. Если такое улучшение наблюдается, то это означает неустойчивость оценок. Пример В случае с функцией расходов на жилье при рассмотрении 1959—1999 гг. как периода выборки и 2000—2003 гг. как периода предсказания, суммы квадратов отклонений для периода выборки, периода предсказания и всего периода равнялись соответственно 0,009673; 0,000012 и 0,011937. Оценивание отдельных регрессий для двух подпериодов «стоит» трех степеней свободы, и число степеней свободы, остающееся после оценивания шести параметров (по два постоянных члена, коэффициента при LGDPI и коэффициента при LGPRHOUS) равно 39. Следовательно, мы получаем следующую F-статистику, распределенную с 3 и 39 степенями свободы:
Критическое значение F(3; 39) на 5%-ном уровне значимости составляет 2,84, так что мы можем сделать вывод о наличии некоторых оснований предполагать нестабильность коэффициентов. На уровне значимости 1% критическое значение составляет 4,31. Таким образом, возможны ситуации, когда тест Чоу на неудачу предсказания и F-тест на устойчивость коэффициентов приводят к разным выводам. Однако даже в этом случае разница между ними не слишком значительная. Тест на неудачу предсказания оказался почти значим на уровне 5%, а тест на стабильность коэффициентов значим на этом уровне с совсем небольшим отклонением от критического значения. Ключевые понятия гипотеза о постоянном доходе лаговая структура модель адаптивных ожиданий модель учета привычек модель частичной корректировки предсказание прогноз простая лаговая структура процесс генерирования данных распределение Койка реализация решетчатый поиск тест Чоу на неудачу предсказания трансформация Койка
|
||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 475; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

 (11.61)
(11.61) (11.62)
(11.62) (11.63)
(11.63)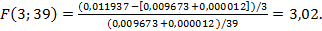 (11.64)
(11.64)


