
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Корреляционно-регрессионные модели. Парная регрессияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
(ПЗ-4 (упражнение) – 2 часа) Учебные цели: 1. Освоить методы корреляционного анализа экономических процессов. 2. Изучить порядок моделирования взаимосвязей экономических показателей. Время проведения: 2 часа. Место проведения и учебно-материальное обеспечение: компьютерный класс со стандартным матобеспечением. Указания на подготовку: а) изучить учебный материал по конспекту лекций и рекомендуемой литературе; б) подготовиться к работе с ППП EXCEL. Учебные вопросы:
1. Методы корреляционного анализа 2. Оценка адекватности линейной парной регрессии 3. Нелинейные модели. Коэффициент детерминации 1-й учебный вопрос. Методы корреляционного анализа Сведения из теории: Для характеристики степени линейной связи между случайными величинами X, Y используются коэффициенты ковариации и корреляции. Коэффициент ковариации определяется как математическое ожидание произведения отклонений случайных величин от их математических ожиданий:
Если случайные величины независимы, коэффициент ковариации равен нулю. При нелинейной связи между случайными величинами коэффициент ковариации также может оказаться равным нулю. Величина коэффициента ковариации зависит от единиц измерения случайных величин. Для получения безразмерного показателя степени линейной связи вводится понятие коэффициента корреляции, определяемого как математическое ожидание нормированных (стандартизованных) случайных величин. Нормированная случайная величина определяется следующим образом:
и имеет нулевое математическое ожидание и единичную дисперсию:
Коэффициент корреляции определяется выражением:
При rXY = 0 линейная связь между случайными величинами отсутствует, но нелинейная связь может иметь место. При rXY =1 имеет место функциональная связь. Выборочные оценки коэффициентов ковариации и корреляции определяются выражениями:
Виды представления корреляционной связи: - корреляционное поле (точечная диаграмма); - корреляционная решетка (матрица); - коэффициент корреляции. Методика корреляционного анализа: 1. Качественный и логический анализ совокупности с целью выяснения причинно-следственной связи. 2. Построение корреляционных матриц или полей для выявления парных взаимосвязанных факторов. 3. Вычисление коэффициентов корреляции между взаимосвязанными факторами для установления силы и направления связи. 4. Оценка достоверности коэффициента корреляции. Достоверность коэффициента корреляция оценивается по критерию Стьюдента:
где rxy - коэффициент корреляции; mr – стандартная ошибка коэффициента корреляции; п - число пар коррелирующих признаков. Полученное эмпирическое значение критерия tэмп должно быть больше табличного значения для уровня значимости 0,05. В этом случае корреляционная взаимосвязь между признаками признается статистически достоверной (значимой). Задание 1.
А. По данным следующей задачи (табл. 3.1) построить график с помощью инструментов EXCEL. Б. Рассчитать коэффициент корреляции, оценить его достоверность и сделать выводы о взаимосвязи числа рекламных объявлений с числом сделок по товару. Функцию КОРРЕЛ не использовать!
Таблица 3.1
2-й учебный вопрос. Оценка адекватности линейной парной регрессии.
Сведения из теории Модель объекта регрессионного анализа имеет вид (рис. 3.1):
Рис. 3.1. На рис.3.1 обозначено: xi - контролируемые входные (независимые, объясняющие) переменные (регрессоры, предикторы, факторы); m - число входных переменных; f (x) - зависимая переменная, обусловленная действием входов xi. Действие неконтролируемых переменных на выходную переменную учитывают введением эквивалентной случайной ошибки ε. В результате действия ошибки ε измеренное значение выходной величины Y отличается от f (x), т.е. Y = f (x)+ ε. Основные предпосылки регрессионного анализа. 1. Входные переменные xi измеряются точно. 2. Входные переменные xi не коррелированы между собой и с ошибкой ε. 3. Ошибка ε является случайной величиной с нулевым математическим ожиданием, дисперсией σ2ε и распределена нормально. Целью регрессионного анализа является определение функциональной зависимости между выходом Y и входными переменными xi. Часто эта зависимость ищется в виде линейного уравнения:
где b 0- свободный член, bi - коэффициенты линейных членов. Наличие случайной ошибки ε проводит к тому, что выходная переменная Y также становится случайной. Поэтому по экспериментальным данным нельзя точно определить значения коэффициентов, а можно найти только их оценки, также являющиеся случайными величинами. С помощью этих оценок можно вычислить и оценку выходной величины Y по уравнению:
называемому уравнением регрессии. Получение регрессионной модели методом регрессионного анализа включает два этапа: 1. Оценка коэффициентов регрессии (чаще всего методом наименьших квадратов). 2. Статистическая оценка значимости коэффициентов регрессии и всего уравнения в целом. Сводка формул для оценки адекватности и точности линейной парной регрессии:
Задание 2. Решите следующую задачу расчетом по приведенным выше формулам. По группе предприятий, выпускающих один и тот же вид продукции, проверяется гипотеза о функции издержек:
где y - издержки производства (тыс. д. е.); x - объем выпуска продукции (тыс. ед.). Исходные данные приведены в табл. 3.2. Таблица 3.2
Требуется: · построить уравнение парной регрессии для связи издержек и объемов производства; · рассчитать линейный коэффициент парной корреляции и коэффициент детерминации. Сделать выводы; · оценить статистическую значимость уравнения регрессии в целом; · оценить статистическую значимость параметров регрессии и корреляции; · выполнить прогноз затрат на производство при прогнозном выпуске продукции, составляющем 195 % от среднего уровня; · оценить точность прогноза, рассчитать ошибку прогноза и его доверительный интервал; 3-й учебный вопрос. Нелинейные модели. Коэффициент детерминации Сведения из теории Различают два класса нелинейных регрессий: 1. Регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, например, полиномы различных степеней, равносторонняя гипербола, полулогарифмическая функция. 2. Регрессии, нелинейные по оцениваемым параметрам, например, степенная, показательная, экспоненциальная. Регрессии нелинейные по включенным переменным приводятся к линейному виду простой заменой переменных, а дальнейшая оценка параметров производится с помощью метода наименьших квадратов. Несколько иначе обстоит дело с регрессиями нелинейными по оцениваемым параметрам, которые делятся на два типа: нелинейные модели внутренне линейные (приводятся к линейному виду с помощью соответствующих преобразований, например, логарифмированием) и нелинейные модели внутренне нелинейные (к линейному виду не приводятся). Задание 3. С помощью функции «Регрессия» в Анализе данных решите следующую задачу. «По предприятиям легкой промышленности региона получена информация, характеризующая зависимость объема выпуска продукции (y, млн. руб.) от объема капиталовложений (x, млн. руб.) (см. следующую таблицу):
1. Используя данные своего варианта, постройте линейную, степенную, показательную, экспоненциальную, полулогарифмическую, гиперболическую и обратную модели. 2. С помощью коэффициента детерминации сравните эти модели. По наилучшей из них: · оцените статистическую значимость уравнения регрессии в целом; · оцените статистическую значимость параметров регрессии; · выполните прогноз затрат на производство при прогнозном выпуске продукции, составляющем 145 % от среднего уровня; · оцените точность осуществленного прогноза, рассчитав стандартную ошибку прогноза и доверительный интервал для вероятности 0,9.
Рис. 3.2. Окно Регрессия
Указание В главном меню выберите Сервис – Анализ данных – Регрессия – ОК. Заполните диалоговое окно ввода данных и параметров вывода (см. рис. 3.2). Входной интервал Y – диапазон, содержащий данные результативного признака; Входной интервал Х – диапазон, содержащий данные факторов независимого признака; Метки – флажок, который указывает, содержит ли первая строка название столбцов или нет; Константа – ноль – флажок, указывающий на наличие или отсутствие свободного члена в уравнении; Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона; Новый рабочий лист – можно задать произвольное имя нового листа.
Задание на самостоятельную работу: Задача 1. Исследуйте связь между спросом и ценой нового товара. Исходные данные приведены в таблице ( (a) Постройте в EXCEL корреляционное поле и оцените тесноту связи между ценой и количеством проданного товара. Сформулируйте гипотезу о форме связи между этими показателями. (b) С помощью инструмента «Регрессия» оцените параметры модели (c) Определите значения стандартной ошибки регрессии и стандартных ошибок коэффициентов. (d) Проверьте адекватность регрессионной модели по статистической значимости коэффициентов. (e) Спрогнозируйте по модели количество проданного товара при условии (f) Как (предположительно) изменятся продажи, если цену единицы товара снизить на 2 у.е.? (g) Определите новые переменные как (h) В чем отличие одной модели от другой? Какую из них вы предпочтете для принятия прогнозных решений? Ответ обоснуйте как с позиций математики, так и с позиций экономической теории.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 578; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.012 с.) |








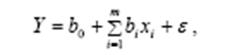
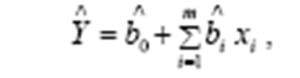






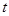 - номер недели,
- номер недели,  - количество проданных единиц товара,
- количество проданных единиц товара,  - цена одной единицы в у.е.).
- цена одной единицы в у.е.).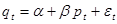 .
.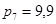 . Оцените ошибку такого прогноза.
. Оцените ошибку такого прогноза. и оцените параметры новой модели
и оцените параметры новой модели 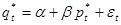 .
.


