
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистическая значимость модели в целом означает, чтоСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
а) для изученного периода расчетные значения результирующего показателя более близки к его истинным значениям, чем его средняя арифметическая величина в этом периоде; б) разница между расчетными и фактическими значениями результирующего показателя для всех точек изученного периода не превышает некоторой наперед заданной величины e; в) разница между расчетными и фактическими значениями результирующего показателя, взятая по абсолютной величине, для всех точек изученного периода не превышает некоторой наперед заданной величины e; г) сумма квадратов ошибок не превышает некоторой, наперед заданной величины e; д) ни одно из предшествующих утверждений не верно.
27. Для количественной оценки тесноты связи используют: а) линейный коэффициент корреляции; б) эмпирическое корреляционное соотношение; в) коэффициент детерминации; г) индекс корреляции.
28. Статистика Дарбина-Уотсона применяется для: а) определения экономической значимости модели в целом; б) определения статистической значимости модели в целом; в) сравнения двух альтернативных вариантов модели; г) определения тесноты связи между результирующими показателем и факторами; д) отбора факторов в модель; е) оценки значимости коэффициента автокорреляции; ж) ни одно из вышеприведенных утверждений не является верным.
29. Статистика Фишера может быть применена для: а) определения экономической значимости модели в целом; б) определения статистической значимости модели в целом; в) сравнения двух альтернативных вариантов модели; г) определения тесноты связи между результирующими показателем и факторами; д) отбора факторов в модель; е) оценки значимости коэффициента автокорреляции; ж) ни одно из вышеприведенных утверждений не является верным.
30. Регрессионное уравнение позволяет: а) установить достоверность различия между показателями; б) устранить неоднородность сравниваемых выборок; в) сравнения двух альтернативных вариантов модели; г) дать количественную оценку взаимосвязи между результирующим показателем и факторами; д) ни одно из вышеприведенных утверждений не является верным.
2-й учебный вопрос – 45 минут. Построение и анализ моделей бинарного выбора Указание: Используя ранее изученный лекционный материал и инструментарий GRETL, до окончания занятия выполнить нижеследующее задание и файл с решением и анализом построенной модели направить по электронной почте на адрес: a.n.mardas@mail.ru. Работы, представленные не в установленный срок, оцениваться не будут!!! Задание. Постройте модель для критерия обоснованности участия администрации региона в поддержке инновационных проектов (Y =1, если поддержка региональных властей присутствовала; Y =0, если поддержка не оказывалась) в связи с ростом доходов Х предприятий (в %). Выборка из 10 предприятий-участников инновационной программы региона дала следующие результаты:
Какое значение роста доходов следует установить пороговым в качестве индикатора реальной инновационной активности предприятия? Занятие 11. Эконометрические модели систем взаимосвязанных уравнений Учебные цели: 1. Совершенствовать навыки анализа экономических процессов 2. Изучить порядок оценивания в условиях точной идентифицируемости Время проведения: 2 часа. Место проведения и учебно-материальное обеспечение: компьютерный класс со стандартным матобеспечением. Указания на подготовку: а) изучить учебный материал по конспекту лекций и рекомендуемой литературе; б) подготовиться к работе с ППП EXCEL и GRETL 1-й учебный вопрос. Практическая реализация двухшагового МНК (2МНК)
Сведения из теории Систему взаимосвязанных тождеств и регрессионных уравнений, в которой переменные могут одновременно выступать как эндогенные (результирующие) в одних уравнениях и как экзогенные (объясняющие) в других, принято называть системой совместных эконометрических уравнений (СЭУ). В уравнения СЭУ могут входить переменные, относящиеся к предшествующим моментам времени, которые называются лаговыми (запаздывающими). Тождества описывают функциональные связи переменных и вытекают из их содержательного экономического смысла. Классический МНК не применим к оцениванию параметров СЭУ, поскольку нарушается предположение о независимости экзогенных и шоковых переменных. Структурная форма СЭУ непосредственно неприменима для решения задач оценивания и прогнозирования, так как уравнения системы не разрешены относительно эндогенных переменных. Поэтому осуществляют преобразование структурной формы СЭУ в так называемую приведённую форму, в которой правые части уравнений не содержат эндогенных переменных. Для оценивания параметров каждого отдельного уравнения структурной формы (в случае наличия сверхидентифицируемых уравнений) разработан специальный двухшаговый МНК (2МНК). Практическая реализация его состоит в следующем. Записывают матричное выражение системы одновременных эконометрических моделей, состоящих из n уравнений с n + m переменными:
где
Пусть известны Т наблюдений за переменными модели (6.1), которые подвержены случайным отклонениям
Для оценивания коэффициентов отдельного уравнения, например, первого:
можно применять МНК, однако оценки в этом случае являются смещенными, в силу корреляции между Yit и Рассмотрим, например, первое уравнение системы:
Поэтому используют 2МНК. Шаг 1. Строим регрессию
Шаг 2. Заменяем y t= Шаг3. Применяем «классический» МНК к уравнению (6.8/)для оценивания параметров
В этом и состоит двухшаговый МНК (2МНК). Полученные по 2МНК оценки будут обладать свойствами асимптотической несмещенности и состоятельности. Изложенное двухэтапное применение процедуры оценивания можно представить в виде одной матричной формулы, для записи которой выберем (без потери общности) первое уравнение:
где
Далее, для замены
где Х – матрица наблюдений за экзогенными переменными системы. Тогда, окончательно
В итоге МНК-оценки для уравнения (6.8’’’) имеют вид:
Задание 1 Используя систему одновременных уравнений монетарной модели
и исходные данные из таблицы
где y 1 - денежная масса; y 2 - оборачиваемость денег; x 2 - совокупный денежный доход населения; x 3 - размер вкладов в системе банков. определить оценки неизвестных параметров b 21, c 21, b 12, c 32. Указание. Проведением пошаговых расчетов по матричным уравнениям компьютерными средствами проверить правильность и обосновать следующее решение:
Задание на самостоятельную работу: Оформить отчет с расчетами и таблицами и подготовиться к его защите, особое внимание уделив содержательному смыслу монетарной модели.
Занятие 12. Эконометрические модели систем взаимосвязанных уравнений. КМНК. Учебные цели: 1. Совершенствовать навыки анализа экономических процессов 2. Изучить порядок оценивания в рамках КМНК. Время проведения: 2 часа. Место проведения и учебно-материальное обеспечение: компьютерный класс со стандартным матобеспечением. Указания на подготовку: а) изучить учебный материал по конспекту лекций и рекомендуемой литературе; б) подготовиться к работе с ППП EXCEL и GRETL 1-й учебный вопрос. Практическая реализация косвенного МНК (КМНК)
Сведения из теории Экономика развивается в условиях эффектов прямой и обратной взаимозависимости и взаимной причинности. Например, численность населения и предложение продуктов питания – переменные, связанные взаимной причинностью. Такой эффект алгебраически описывается следующим образом:
Система эконометрических уравнений (CЭУ) вида (1.1), (1.2) может описывать, например, зависимость Y1t – спроса на птицу, Y2t – цены на птицу от X1t – дохода потребителей, X2t – цены на товар заменитель (говядину) и X3t – цены на корм птицы. Тогда первое уравнение системы (1.1) отражает поведение потребителей, а второе (1.2) – поставщиков птицы. Система (1.1), (1.2) относится к структурным СЭУ, поскольку результирующая переменная первого уравнения является объясняющей второго и наоборот. Структурная форма СЭУ непосредственно неприменима для решения задач оценивания и прогнозирования, так как уравнения системы не разрешены относительно эндогенных переменных. Поэтому осуществляют преобразование структурной формы СЭУ в приведенную форму, в которой правые части уравнений не содержат эндогенных переменных. Осуществим такое преобразование на примере системы (1.1, 1.2). Вначале, подставив вместо
Тогда, разрешив уравнение относительно
Выполним аналогичные преобразования для уравнения (1.2) и, разрешая его относительно
В общепринятом в литературе виде приведенная форма СЭУ для (1.1, 1.2) записывается так:
Здесь уже справедливо гипотеза о независимости шоковой vjt и экзогенных переменных, и для оценивания мультипликаторов можно применить МНК, который носит название косвенного МНК, так как строит оценки для π, по которым надо еще пересчитать оценки a и b. Например, для рассмотренного примера:
На практике для СЭУ преобразование в приведенную форму алгебраически не всегда возможно. Поэтом для уяснения ситуации применяют порядковый критерий проверки каждого уравнения СЭУ на идентифицируемость. Порядковый критерий (ПК) является необходимым, но недостаточным условием идентификации СЭУ, для его формулировки необходимо ввести: mi – число предопределенных переменных в i - ом уравнении, m – общее число предопределенных переменных в СЭУ (экзогенных и лаговых эндогенных); ni – число эндогенных переменных СЭУ в её i -ом уравнении. Порядковый критерий: Если число предопределенных переменных СЭУ, не включенных в i -ое уравнение не меньше, чем число эндогенных переменных СЭУ, содержащихся в анализируемом уравнении, уменьшенное на единицу, то данное уравнение считают идентифицируемым. Различают: а) точную идентификацию, если б) сверхидентификацию, если в) неидентифицируемость, если Задание 1 По системе совместных уравнений
в которой y 1 и y 2 - эндогенные переменные, x 2 – экзогенная переменная, а x 1 t =1, t =1,2,...,5, собраны следующие данные наблюдений над переменными модели:
1) Представьте систему в матричном виде и проведите проверку идентифицируемости каждого уравнения по порядковому критерию. 2) Запишите в явном матричном виде приведенную форму исходной системы (6.10.1), (6.10.2). 3) Оцените (косвенным МНК) параметры уравнения (6.10.1). 4) Пусть априорно известно, что 5) Используйте двухшаговый МНК для оценивания параметра
|
|||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 816; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.012 с.) |


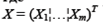 - вектор предопределенных (экзогенных и лаговых эндогенных) переменных;
- вектор предопределенных (экзогенных и лаговых эндогенных) переменных;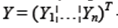 - вектор эндогенных переменных;
- вектор эндогенных переменных; - матрица коэффициентов, в которой bij - коэффициент при переменной yi в i -ом уравнении;
- матрица коэффициентов, в которой bij - коэффициент при переменной yi в i -ом уравнении;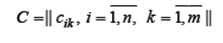 - матрица коэффициентов при переменной xk, в которой cik - коэффициент при переменной
- матрица коэффициентов при переменной xk, в которой cik - коэффициент при переменной 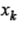 в i - ом уравнении;
в i - ом уравнении; - нулевой вектор.
- нулевой вектор. , тогда:
, тогда:
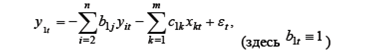
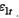
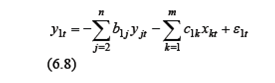
 эндогенных переменных
эндогенных переменных 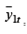 , на переменные, входящие в правую часть уравнения (6.8), и находим МНК-оценки
, на переменные, входящие в правую часть уравнения (6.8), и находим МНК-оценки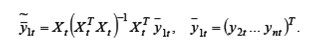
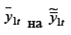 в уравнении (6.8):
в уравнении (6.8):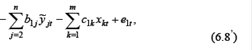
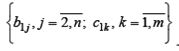
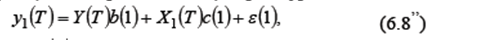
 - вектор наблюдений за эндогенной переменной, подлежащей определению в данном уравнении
- вектор наблюдений за эндогенной переменной, подлежащей определению в данном уравнении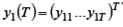
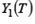 - матрица наблюдений над эндогенными переменными, объясняющими поведение y 1:
- матрица наблюдений над эндогенными переменными, объясняющими поведение y 1: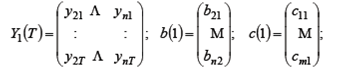
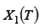 - матрица наблюдений за экзогенными переменными первого уравнения. Предполагается, что избранное уравнение для обеспечения состоятельности оценок идентифицируемо по порядковому критерию: «Для того чтобы уравнение модели было идентифицируемо, необходимо, чтобы число предопределенных переменных, не входящих в уравнение, было не меньше «числа эндогенных переменных, входящих в уравнение минус 1»
- матрица наблюдений за экзогенными переменными первого уравнения. Предполагается, что избранное уравнение для обеспечения состоятельности оценок идентифицируемо по порядковому критерию: «Для того чтобы уравнение модели было идентифицируемо, необходимо, чтобы число предопределенных переменных, не входящих в уравнение, было не меньше «числа эндогенных переменных, входящих в уравнение минус 1»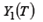 на оценку
на оценку 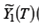 проведем следующие преобразования:
проведем следующие преобразования:
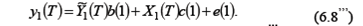




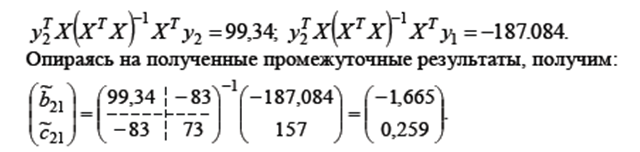
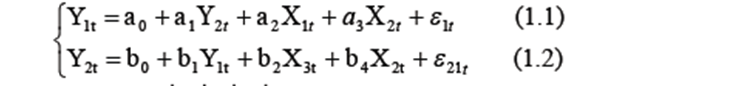
 его выражение из уравнения (1.2), получим:
его выражение из уравнения (1.2), получим: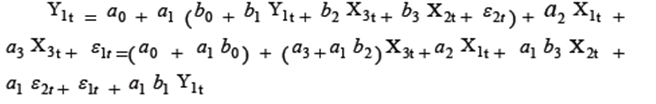
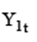 , получим:
, получим: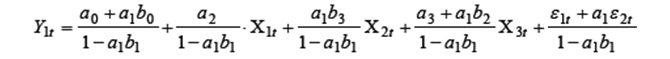
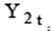 , будем иметь:
, будем иметь: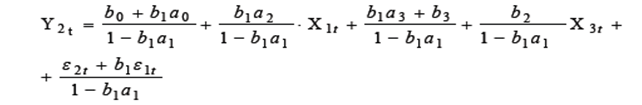
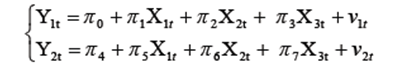


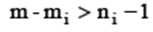 ;
;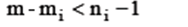 .
.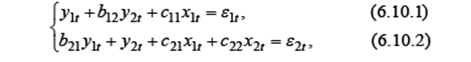

 . Как изменится вывод об идентифицируемости этого уравнения?
. Как изменится вывод об идентифицируемости этого уравнения? первого уравнения системы.
первого уравнения системы.


