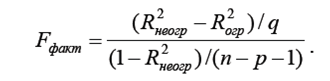Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Y - зависимая переменная (результативный признак),Содержание книги
Поиск на нашем сайте
x1, x2,..., хm – независимые, объясняющие, переменные (признак-факторы), ε - возмущение или стохастическая переменная, включающая влияние неучтенных в модели факторов. Основные типы функций, используемые при количественной оценке связей: Линейная функция: y=a0+а1 x1 +а2 x2 +,..., +аm хm; Параметры а1 , а2,… аm называются коэффициентами «чистой» регрессии и характеризуют среднее изменение результата с изменением соответствующего фактора на единицу при неизменном значении других факторов, закрепленных на среднем уровне. Нелинейные функции: y=a x1b1x2b2 ... хm b m –степенная функция; b1,b2,…,bm - коэффициенты эластичности; показывают на сколько % изменится в среднем результат при изменении соответствующего фактора на 1% и при неизменности действия других факторов. Обозначим: X - прямоугольная матрица наблюдений независимых переменных размерностью n (n - число наблюдений) на (m +1) - число оцениваемых коэффициентов, включая свободный член.
Для нахождения МНК – оценок коэффициентов регрессии, как и прежде, минимизируют остаточную сумму квадратов:
Истинное значение коэффициента регрессии Сводка формул для множественной регрессии: Оценка коэффициента множественной детерминации
где ∆ и ∆1 – определители матрицы парных коэффициентов корреляции и расширенной матрицы парных коэффициентов корреляции.
F – критерий значимости уравнения в целом
t – критерий значимости коэффициентов регрессии
После определения точечных оценок коэффициентов теоретического уравнения регрессии могут быть рассчитаны интервальные оценки коэффициентов. Доверительный интервал, накрывающий с доверительной вероятностью
Здесь
Проще всего провести построение множественной регрессии с помощью с помощью инструмента анализа данных Регрессия. Для этого выполняют команду Сервис-Анализ данных-Регрессия-OK.
Задание 1. В табл. 4.1 приведены данные за 11 дней о курсе доллара (x1 руб.), фондовом индексе (x2) и котировке акций (y, ден. ед.).
Таблица 4.1
Требуется: 1) построить уравнение множественной линейной регрессии и дать экономическую интерпретацию коэффициентов уравнения; 2) оценить стандартную ошибку регрессии и стандартные ошибки коэффициентов; 3) построить доверительные интервалы для коэффициентов регрессии, соответствующие доверительной вероятности 4) оценить статистическую значимость коэффициентов регрессии с помощью t -критерия при уровне значимости 5) оценить на уровне 0,05 полученное уравнение на основе коэффициента детерминации и F - критерия Фишера; 6) сделать выводы по качеству построенной модели. Метод исключения в проверке спецификации модели При выборе формы спецификации модели первоначально рассматривается уравнение множественной линейной регрессии y = β0 + β1x1 + β2x2 + …+ βnxn + ε (1) Для перехода к адекватной форме модели далее применяется алгоритм пошагового регрессионного анализа методом исключения переменных. При этом выполняются следующие действия: · строится регрессионная модель методом наименьших квадратов; · оценивается значимость коэффициентов регрессии; · выявляется наличие зависимости между факторными признаками путем анализа матрицы парных коэффициентов корреляции и матрицы частных коэффициентов корреляции; · строится новое уравнение регрессии с исключением незначимых и части взаимно коррелирующих переменных. При этом из числа коррелирующих переменных в модели оставляют те, которые более соответствуют ее экономическому содержанию, либо те, которые имеют наибольшее значение частной корреляции с зависимой переменной. Задание 2. Имеются следующие данные по 20 сельскохозяйственным районам: Y – урожайность зерновых культур (ц/га); X1 – число колесных тракторов (приведенной мощности) на 100 га; X2 – число зерноуборочных комбайнов на 100 га; X3 – число орудий поверхностной обработки почвы на 100 га; X4 – количество удобрений, расходуемых на гектар;
X5 – количество химических средств оздоровления растений, расходуемых на гектар. Требуется провести пошаговый регрессионный анализ урожайности Y на основе исходных данных (табл. 1) Таблица 1 Исходные данные
Указание: для окончательного выбора модели воспользуйтесь критерием Фишера в отношении коэффициентов сравниваемых спецификаций. Для этого рассчитывают статистику
Здесь используются коэффициенты детерминации из регрессии первоначальной (неогр) и регрессии с исключенными переменными (огр), причем q – число исключений, n – число наблюдений, p – число факторов в исходной регрессии. Находят табличное (критическое) значение F табл со степенями свободы q и n - p – 1. Если F факт > F табл, то нулевая гипотеза отклоняется в пользу альтернативной: имеющиеся данные противоречат гипотезе об эквивалентности моделей.
2-й учебный вопрос. Основы обработки данных в GRETL Подготовка данных в Excel для импорта в GRETL Создайте новую рабочую книгу Excel. Убедитесь, что все импортируемые данные расположены на одном листе с названием без символов кириллицы или со стандартным названием (Лист1 для русифицированной версии Excel). Данные должны быть размещены в столбцах (или строках) без пропусков ячеек. Не допускайте также объединения ячеек импортируемого столбца (строки). В первой ячейке столбца (строки) укажите имя переменной (без символов кириллицы), которое понадобится для импорта данного столбца (строки) в G RETL. Желательно сразу указывать такие имена рядов данных, по которым можно будет легко идентифицировать импортируемую переменную в дальнейшем при работе с ней в GRETL. Установите формат импортируемых ячеек на «Общий», проверьте отсутствие нечисловых значений в ячейках: текста, значений со знаком процента «%» и т.п. Сохраните рабочую книгу Excel в формате Excel с именем файла без символов кириллицы.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 380; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.117.172 (0.007 с.) |


 - вектор наблюденных значений зависимой переменной размерностью n.
- вектор наблюденных значений зависимой переменной размерностью n.
 - вектор искомых оценок коэффициентов регрессии размерностью (m + 1).
- вектор искомых оценок коэффициентов регрессии размерностью (m + 1).
 отличается от его оценки. Может иметь место случай, когда оценка отличается от нуля, хотя истинное значение коэффициента равно нулю. В этом случае xi не влияет на выход, а про коэффициент bi говорят, что он незначимо отличается от нуля. Незначимые коэффициенты исключают из уравнения регрессии, а оставшиеся оценки пересчитывают.
отличается от его оценки. Может иметь место случай, когда оценка отличается от нуля, хотя истинное значение коэффициента равно нулю. В этом случае xi не влияет на выход, а про коэффициент bi говорят, что он незначимо отличается от нуля. Незначимые коэффициенты исключают из уравнения регрессии, а оставшиеся оценки пересчитывают.
 .
.

 =1−α неизвестное значение параметра
=1−α неизвестное значение параметра  , определяется неравенством
, определяется неравенством
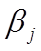




 ;
; ;
;