
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Показатели экономических процессов как случайные величиныСодержание книги
Поиск на нашем сайте
Показатели экономических процессов как случайные величины (ПЗ-1 (упражнение) – 2 часа) Учебные цели: 1. Проверить уровень знаний по основам математической статистики, изученным в ходе предшествующей подготовки и материала, доведенного на лекциях. 2. Учить порядку обработки результатов статистического наблюдения за показателями экономических процессов.
Учебные вопросы: 1. Выборочный метод в экономике. 2. Проверка нормальности распределения выборочных данных. Время проведения: 2 часа. Место проведения и учебно-материальное обеспечение: компьютерный класс со стандартным матобеспечением. Метод проведения: упражнение. Применение параметрических и непараметрические критериев к оценке статистических гипотез (ПЗ-2,3 (упражнение) – 4 часа) Учебные цели: 1. Закрепить знания по основам математической статистики, изученным в ходе предшествующей подготовки, и материал, доведенный на лекциях. 2. Изучить порядок обработки результатов статистического наблюдения.
Учебные вопросы: 1. Нормальное распределение и статистические оценки 2. Статистические распределения и их применение в экономических исследованиях. Непараметрические методы в анализе экономических процессов. Время проведения: 2+2 часа. Место проведения и учебно-материальное обеспечение: компьютерный класс со стандартным матобеспечением. Метод проведения: упражнение. 1-й учебный вопрос. Нормальное распределение и статистические оценки
Используя навыки предшествующего занятия самостоятельно решить следующую задачу: «Служба маркетинга фирмы анализирует продажи. Сведения об объеме ежедневных продаж товара (в тыс. ден. ед.) за последние 100 дней приведены для каждого варианта в прил. 1. 1.Построить: интервальный вариационный ряд; полигон и гистограмму (на одном рисунке); кумуляту (на другом рисунке). 2.Вычислить выборочные характеристики: среднее, дисперсию, среднее квадратическое отклонение, коэффициент вариации, асимметрию, эксцесс, моду, медиану. 3. Заменив параметры нормального закона распределения их выборочными характеристиками, рассчитать и построить графики функции плотности и функции распределения нормального закона, наложив эти графики соответственно на полигон и кумуляту.
ПРИЛОЖЕНИЕ 1 Исходные данные для построения интервального вариационного ряда, оценивания нормального закона распределения и его параметров (разделитель между числами - пробел) 1 вариант 0,91 0,62 1,07 1,38 1,36 1,52 0,34 0,93 1,33 0,67 0,79 0,49 0,45 0,71 0,77 0,36 0,83 0,88 1,04 0,89 0,90 0,89 1,40 0,97 0,94 0,85 1,59 1,26 1,71 0,80 1,50 0,52 1,16 1,27 1,58 0,97 0,84 1,20 0,89 1,23 0,57 0,75 0,54 0,89 0,99 1,01 0,90 1,66 0,48 0,78 0,23 1,43 0,62 0,80 1,23 1,14 1,26 1,18 0,59 0,67 1,21 1,10 0,72 0,93 1,04 1,17 1,04 0,73 1,57 1,15 1,02 1,25 1,26 0,81 0,72 1,33 0,64 0,53 1,21 1,19 1,66 1,43 1,39 1,03 1,00 1,14 0,99 0,68 0,47 1,25 1,13 1,19 1,06 0,69 1,37 0,91 0,75 0,75 0,87 0,86 2 вариант 2,39 1,80 1,91 1,64 1,91 0,66 1,92 1,20 2,09 2,30 2,79 1,63 1,55 2,09 1,86 1,88 2,95 2,02 1,91 3,10 1,62 2,76 1,99 1,96 2,97 2,22 2,26 1,86 2,41 1,96 1,56 1,34 2,12 1,41 3,16 1,92 1,05 1,80 2,57 1,77 1,61 1,18 2,19 1,90 2,34 1,62 1,79 2,17 1,80 2,13 0,52 1,96 2,15 3,27 1,08 1,06 0,62 2,70 3,42 1,77 1,40 2,33 2,40 1,49 2,49 2,40 1,88 1,07 2,61 2,46 1,79 1,59 2,52 2,21 2,33 3,25 2,16 1,34 2,29 1,26 2,34 1,91 2,18 2,21 2,08 1,84 1,19 3,27 2,96 2,63 1,11 1,33 2,32 2,04 1,99 2,10 0,87 1,85 1,44 1,40 3 вариант 2,54 3,42 3,32 2,92 2,90 3,81 1,47 1,46 3,52 4,64 1,52 4,12 3,87 3,82 2,53 2,98 3,36 2,95 5,26 2,24 3,65 3,55 3,60 3,63 3,22 3,58 1,73 1,34 4,03 4,33 2,94 4,01 3,25 1,74 3,29 3,08 2,90 2,81 3,95 3,20 3,41 3,67 2,34 3,29 3,16 3,00 2,89 3,72 3,15 2,55 4,71 2,86 3,71 3,33 2,97 4,38 2,76 3,74 2,25 4,03 2,96 2,79 0,51 3,52 3,65 2,94 1,00 2,42 4,05 3,12 3,21 3,61 3,18 2,65 2,50 2,13 3,20 2,35 3,72 2,94 2,80 5,11 2,76 2,62 3,98 2,60 1,63 1,97 3,20 2,76 3,03 3,50 2,83 4,14 2,93 3,93 3,76 1,17 3,12 3,33 4 4,95 4,03 4,16 5,09 3,10 4,78 3,64 2,96 3,02 3,61 2,64 1,44 4,55 5,11 3,04 3,83 3,61 4,77 4,28 3,85 3,52 4,27 4,18 4,12 3,74 3,53 3,54 2,08 5,85 3,62 2,47 3,79 4,25 2,97 2,76 3,66 3,81 3,37 3,28 3,69 3,09 4,39 5,11 3,56 5,47 5,68 3,51 5,39 3,62 4,12 4,53 2,37 5,07 6,73 2,36 3,59 6,53 4,65 3,92 5,59 3,15 3,57 2,61 3,99 4,85 3,20 2,52 3,90 3,58 1,06 5,22 2,90 4,48 3,06 5,06 6,24 5,21 2,79 6,73 5,86 5,89 3,27 2,03 4,12 4,61 4,21 5,10 3,42 6,01 4,17 1,84 4,69 5,18 5,79 6,09 3,78 3,76 4,37 5,21 2,04 5 5,73 5,87 3,14 4,29 5,37 4,77 3,35 3,11 4,45 5,49 5,89 3,70 5,12 5,97 5,26 6,61 5,95 3,45 4,53 7,68 6,98 7,99 5,16 5,28 5,35 6,26 3,22 5,68 7,57 4,26 8,23 3,99 5,44 4,69 5,56 5,25 7,80 6,69 5,12 6,62 3,77 6,67 3,88 4,18 5,43 6,08 5,12 4,56 4,44 4,38 6,03 6,09 4,60 5,77 3,43 4,92 5,68 4,24 7,00 5,53 4,00 3,91 5,39 5,99 5,13 2,89 4,91 4,58 3,99 5,66 5,13 5,62 4,37 1,40 6,09 2,54 4,65 5,17 4,97 3,02 7,00 4,16 3,51 5,23 5,68 6,08 5,19 4,91 1,90 4,64 6,20 5,92 9,01 4,43 2,34 5,32 2,14 3,79 4,36 6,51 Указание. Задачу решить в пакете EXCEL. 2-й учебный вопрос. Статистические распределения и их применение в экономических исследованиях Задание 1. С помощью t -теста решите следующую задачу. По имеющимся данным H 0: MX =120 при H 1: MX ¹ 120. Задание 2. Проверьте расчетами правильность ответа в следующей задаче:
«По данным: Ответ: Поскольку расчетное значение критерия меньше табличного, то H 0отвергается с уровнем значимости 5%.» Сведения из теории:
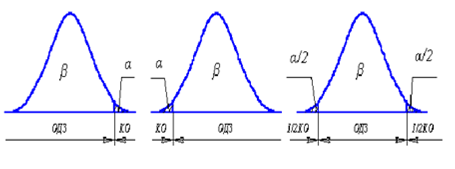
Статистической называется гипотеза о виде неизвестного распределения либо о параметрах известного распределения. Например, требуется проверить гипотезу о равенстве математического ожидания MX гипотетическому значению C. Проверяемую гипотезу называют нулевой и обозначают H 0. Гипотезу, противоречащую нулевой, называют конкурирующей (альтернативной) и обозначают H 1. Конкурирующие гипотезы могут быть трех типов. Например, для H 0: MX = C могут применяться следующие альтернативные гипотезы: · H 1: MX > C («больше чем») – положительное отклонение оцениваемого параметра MX от гипотетического значения С; · H 2: M X < C («меньше чем») – отрицательное отклонение оцениваемого параметра MX от гипотетического значения С; · H 3: M X ≠ C («не равно») – отклонение оцениваемого параметра MX от гипотетического значения С по абсолютной величине. Статистические гипотезы проверяются с помощью критериев значимости, представляющих неравенства. Построение критерия значимости так же, как и построение доверительного интервала требует знания закона распределения оценки, используемой для этой цели. Для построения критерия значимости весь диапазон изменения величины, относительно которой проверяется H 0, разбивается на две области: область допустимых значений (ОДЗ) и критическую область (КО). При этом в зависимости от вида альтернативной гипотезы следует использовать критическую область трех типов: правостороннюю для H 1 (рис.1), левостороннюю для H 2 (рис.2) и двустороннюю для H 3 (рис.3).
Рис. 1. Рис. 2. Рис.3.
При попадании проверяемой величины в ОДЗ принимается H 0, а при ее попадании в КО H 0 отвергается и принимается альтернативная гипотеза H 1. Области допустимых значений соответствует вероятность β, а критической области – вероятность α =1− β, называемая уровнем значимости критерия. Уровень значимости критерия α есть вероятность попадания в КО в случае, когда справедлива H 0 или, что то же самое, вероятность отвергнуть H 0, когда она верна, а β - вероятность принятия H 0 в случае ее справедливости. Уровень значимости принято выражать в процентах. Обычно принимают α= 5%. Например, проверка гипотезы о равенстве математического ожидания гипотетическому значению по критерию Стьюдента проводится по соотношению
где t α - квантиль распределения Стьюдента для числа степеней свободы n −1 и уровня значимости критерия α при правосторонней критической области. При невыполнении данного условия принимается альтернативная гипотеза H 1. Проверка гипотезы о равенстве двух дисперсий проводится по критерию Фишера:
где f - квантиль распределения Фишера для степеней свободы n 1−1 и n 2−1 при уровне значимости α. Практические рекомендации Для получения решения используйте окно статистических функций в EXCEL. 2-й учебный вопрос. Непараметрические методы в анализе экономических процессов. Задание 3. Установить достоверность различий в предпочтениях потребителей по отношению к новому товару. Ряд X – контрольная выборка (число сделок по традиционному товару ежедневно). Ряд Y – опытная выборка (число сделок ежедневно по инновационному товару). X: 6, 25, 25, 30, 38, 39, 44 (nx =7). Y: 8,30, 32, 41, 41, 46, 68, 100 (ny =8). Необходимо определить достоверность различий в уровне продаж (предпочтениях потребителей).
Сведения из теории Чаще всего установить характер распределения показателя не удается, а, следовательно, и установить параметры распределения нельзя. В этом случае приходится прибегать к непараметрическим критериям как основному методу разрешения проблемы.
Q-критерий Розенбаума используют для оценки различий между двумя выборками по уровню какого-либо признака, количественно измеренного. В каждой из выборок должно быть не менее 11 данных. Если Q -критерий выявляет различия между выборками с уровнем значимости р = 0,01, то можно ограничиться только им и избежать трудностей применения других критериев. Содержательная формулировка статистических гипотез будет следующей: Н 0: Уровень признака в выборке 1 не превышает уровня признака в выборке 2. Н 1: Уровень признака в выборке 1 превышает уровень признака в выборке 2. Алгоритм: 1. Проверяют выполнимость ограничений 2. Упорядочивают значения отдельно в каждой выборке по степени возрастания анализируемого показателя. Принимают за выборку 1 ту, значения в которой предположительно выше. 3. Определяют самое высокое (максимальное) значение показателя в выборке 2 (в которой значения предположительно ниже) и подсчитывают количество значений показателя в выборке 1, которые выше максимального значения в выборке, обозначая полученную величину как S 1. 4. Определяют самое низкое (минимальное) значение показателя в выборке 1 и подсчитывают количество значений в выборке 2, которые ниже минимального значения выборки 1. Обозначают полученную величину как S 2. 5. Подсчитывают эмпирическое значение критерия по формуле Qэмп = S 1 + S 2 и с помощью таблицы определяют критические значения Qкр для данных n 1 и n 2. Если Qэмп при уровне значимости 0,05 превышает Qкр, то гипотеза Н о отвергается. Сравнение двух независимых выборок (опытной и контрольной) с помощью критерия Колмогорова-Смирнова Применение критерия Колмогорова-Смирнова основано на предположении, что если сравниваемые группы наблюдения представляют собой выборки из одной совокупности, то ранги отдельных вариант обеих групп при объединении в один ранжированный ряд должны передаваться. Критерий основан на сопоставлении рядов накопленных частостей сравниваемых групп и нахождении наибольшей абсолютной разности между ними. Алгоритм критерия состоит в следующем. 1. Объединяются в один ряд в возрастающем порядке все варианты сравниваемых выборок (групп). 2. Записывают частоты вариант для одной и другой групп. 3. Представляют частоты в накопленном виде (Sx и Sy). 4. Определяют накопленные частости, т.е. накопленные частоты делят на число наблюдений (Sx / nx и Sy / ny).
5. Вычисляют разности накопленных частостей групп x и y без учета знаков | Sx / nx - Sy / ny |. 6. Находят максимальную разность D. 7. Определяют критерий
8. Сравнивают полученное значение λ2 с граничным λ20,05 . Если найденная λ2 > λ20,05, различия признаются существенными, в противном случае принимается Н 0-гипотеза, т.е. различия признаются несущественными. Практические рекомендации Задачу решите методом Колмогорова-Смирнова. Задание на самостоятельную работу: Задание 2.1. В ходе тестирования 20 кандидатов на должность секретаря установлено, что в среднем они тратили 7 минут на набор одной страницы сложного текста на компьютере при выборочном стандартном отклонении S = 2 минуты. Считая, что время (X)набора текста имеет нормальный закон распределения: а) Определите 95%-й доверительный интервал для математического ожидания тх. б) Оцените количество претендентов на работу, которые набрали текст быстрее, чем за 5 минут. в) Предполагалось, что среднее время набора страницы текста должно составить 5,5 минуты. Не противоречат ли полученные данные этой гипотезе? Задание 2.2 Моделирование продолжительности инновационного проекта проведено двумя способами: методом PERT и методом Монте-Карло. При этом получены следующие значения выборочных дисперсий времени завершения проекта: s 12 = 28,4 дн. 2 (для метода Монте-Карло из трех модельных прогонов) и s 2 2 = 16,5 дн. 2 (для метода PERT c 13 работами на критическом пути). Оцените гипотезу об одинаковой адекватности моделей. Задание 3.1. Сравнивается эффективность четырех разных методик контроля качества продукции. Для этой цели избраны четыре разных метода измерения точностных характеристик. Эффективность методик оценивалась по сумме зафиксированных несоответствий в течение семи дней (см. табл. 4.4). Проверьте гипотезу об отсутствии влияния регулируемого фактора (метода измерения) на действенность системы контроля.
Таблица 4.4 Эмпирические данные о несоответствиях, выявленные различными методами контроля
Указание. Для решения используйте χ2-критерий. Задание 3.2. В табл. 3. представлены данные об общей стоимости (в тыс. ден. ед.) туров, проданных за последний месяц сотрудниками туристического агентства — восемью женщинами и девятью мужчинами.
Таблица 3 Женщины 11 12 16 13 18 15 13 14 n 1 = 8 Мужчины 7 10 14 15 12 16 14 12 12 n 2 = 9 Создается впечатление, что женщинам лучше удается продавать туры, чем мужчинам. Проверить это предположение количественно на 5%-ном уровне значимости.
Отчет по требованиям ГОСТа в печатном виде представлять на очередное практическое занятие (по занятию 2 – на третье, по занятию три – по вопросам 2 и 3 – на четвертое).
Где Таблица 1
Исходные данные
Указание: для окончательного выбора модели воспользуйтесь критерием Фишера в отношении коэффициентов сравниваемых спецификаций. Для этого рассчитывают статистику
Здесь используются коэффициенты детерминации из регрессии первоначальной (неогр) и регрессии с исключенными переменными (огр), причем q – число исключений, n – число наблюдений, p – число факторов в исходной регрессии. Находят табличное (критическое) значение F табл со степенями свободы q и n - p – 1. Если F факт > F табл, то нулевая гипотеза отклоняется в пользу альтернативной: имеющиеся данные противоречат гипотезе об эквивалентности моделей.
2-й учебный вопрос. Основы обработки данных в GRETL Подготовка данных в Excel для импорта в GRETL Создайте новую рабочую книгу Excel. Убедитесь, что все импортируемые данные расположены на одном листе с названием без символов кириллицы или со стандартным названием (Лист1 для русифицированной версии Excel). Данные должны быть размещены в столбцах (или строках) без пропусков ячеек. Не допускайте также объединения ячеек импортируемого столбца (строки). В первой ячейке столбца (строки) укажите имя переменной (без символов кириллицы), которое понадобится для импорта данного столбца (строки) в G RETL. Желательно сразу указывать такие имена рядов данных, по которым можно будет легко идентифицировать импортируемую переменную в дальнейшем при работе с ней в GRETL. Установите формат импортируемых ячеек на «Общий», проверьте отсутствие нечисловых значений в ячейках: текста, значений со знаком процента «%» и т.п. Сохраните рабочую книгу Excel в формате Excel с именем файла без символов кириллицы. Занятие 6. Занятие 7. Занятие 9. Автокорреляции верны? a) Оценки дисперсий МНК-оценок параметров оказываются заниженными, что влечет неверные выводы о значимости переменных b) МНК-оценки параметров остаются несмещенными c) Оценка дисперсии случайной переменной – смещена d) Все ответы верны Переменных? a) В смещении оценок параметров при включенных в модель переменных b) В увеличении дисперсии оценок параметров модели c) В уменьшении коэффициента детерминации d) В уменьшении t-статистик параметров модели
Значение 2.4? a) Рассматриваемый параметр статистически значим b) Рассматриваемый параметр в 2 раза больше порогового значения c) Рассматриваемый параметр статистически не значим d) Рассматриваемым параметром можно пренебречь
До 0.95? a) Доверительные интервалы расширяются, пороговые значения t-статистик возрастают b) Доверительные интервалы расширяются, пороговые значения t-статистик уменьшаются c) Доверительные интервалы сужаются пороговые значения t- статистик возрастают d) Доверительные интервалы сужаются пороговые значения t-статистик уменьшаются
До 0.90? a) Доверительные интервалы сужаются пороговые значения t- статистик уменьшаются b) Доверительные интервалы расширяются, пороговые значения t-статистик возрастают c) Доверительные интервалы расширяются, пороговые значения t-статистик уменьшаются d) Доверительные интервалы сужаются пороговые значения t-статистик возрастают
Делится на три части? a) Голдфилда-Квандта b) Спирмена c) Бриша-Пагана d) Лагранжа
Какие утверждения верны? a) Наблюдаемое значение t-статистики некоторого параметра модели зависит от значения самого параметра и несмещенной дисперсии данной случайной величины b) Наблюдаемое значение t-статистики некоторого параметра модели зависит только от значения самого параметра c) Наблюдаемое значение t-статистики некоторого параметра модели зависит только от несмещенной дисперсии соответствующей случайной величины d) Наблюдаемое значение t-статистики некоторого параметра модели не зависит ни от значения самого параметра, ни от несмещенной дисперсии данной случайной величины
Критерия Рамсея? a) Построение расширенной модели, в которую включены старшие степени эндогенной переменной b) Произведение коэффициентов корреляции пропущенной переменной и остальных переменных модели c) Выбор только тех переменных, оценки параметров которых положительны d) Выбор только тех переменных, оценки параметров которых больше критических
Занятие 11. Эконометрические модели систем взаимосвязанных уравнений Учебные цели: 1. Совершенствовать навыки анализа экономических процессов 2. Изучить порядок оценивания в условиях точной идентифицируемости Время проведения: 2 часа. Место проведения и учебно-материальное обеспечение: компьютерный класс со стандартным матобеспечением. Указания на подготовку: а) изучить учебный материал по конспекту лекций и рекомендуемой литературе; б) подготовиться к работе с ППП EXCEL и GRETL 1-й учебный вопрос. Практическая реализация двухшагового МНК (2МНК)
Сведения из теории Систему взаимосвязанных тождеств и регрессионных уравнений, в которой переменные могут одновременно выступать как эндогенные (результирующие) в одних уравнениях и как экзогенные (объясняющие) в других, принято называть системой совместных эконометрических уравнений (СЭУ). В уравнения СЭУ могут входить переменные, относящиеся к предшествующим моментам времени, которые называются лаговыми (запаздывающими). Тождества описывают функциональные связи переменных и вытекают из их содержательного экономического смысла. Классический МНК не применим к оцениванию параметров СЭУ, поскольку нарушается предположение о независимости экзогенных и шоковых переменных. Структурная форма СЭУ непосредственно неприменима для решения задач оценивания и прогнозирования, так как уравнения системы не разрешены относительно эндогенных переменных. Поэтому осуществляют преобразование структурной формы СЭУ в так называемую приведённую форму, в которой правые части уравнений не содержат эндогенных переменных. Для оценивания параметров каждого отдельного уравнения структурной формы (в случае наличия сверхидентифицируемых уравнений) разработан специальный двухшаговый МНК (2МНК). Практическая реализация его состоит в следующем. Записывают матричное выражение системы одновременных эконометрических моделей, состоящих из n уравнений с n + m переменными:
где
Пусть известны Т наблюдений за переменными модели (6.1), которые подвержены случайным отклонениям
Для оценивания коэффициентов отдельного уравнения, например, первого:
можно применять МНК, однако оценки в этом случае являются смещенными, в силу корреляции между Yit и Рассмотрим, например, первое уравнение системы:
Поэтому используют 2МНК. Шаг 1. Строим регрессию
Шаг 2. Заменяем y t= Шаг3. Применяем «классический» МНК к уравнению (6.8/)для оценивания параметров
В этом и состоит двухшаговый МНК (2МНК). Полученные по 2МНК оценки будут обладать свойствами асимптотической несмещенности и состоятельности. Изложенное двухэтапное применение процедуры оценивания можно представить в виде одной матричной формулы, для записи которой выберем (без потери общности) первое уравнение:
где
Далее, для замены
где Х – матрица наблюдений за экзогенными переменными системы. Тогда, окончательно
В итоге МНК-оценки для уравнения (6.8’’’) имеют вид:
Задание 1 Используя систему одновременных уравнений монетарной модели
и исходные данные из таблицы
где y 1 - денежная масса; y 2 - оборачиваемость денег; x 2 - совокупный денежный доход населения; x 3 - размер вкладов в системе банков. определить оценки неизвестных параметров b 21, c 21, b 12, c 32. Указание. Проведением пошаговых расчетов по матричным уравнениям компьютерными средствами проверить правильность и обосновать следующее решение:
Задание на самостоятельную работу: Оформить отчет с расчетами и таблицами и подготовиться к его защите, особое внимание уделив содержательному смыслу монетарной модели.
Занятие 12. Эконометрические модели систем взаимосвязанных уравнений. КМНК. Учебные цели: 1. Совершенствовать навыки анализа экономических процессов 2. Изучить порядок оценивания в рамках КМНК. Время проведения: 2 часа. Место проведения и учебно-материальное обеспечение: компьютерный класс со стандартным матобеспечением. Указания на подготовку: а) изучить учебный материал по конспекту лекций и рекомендуемой литературе; б) подготовиться к работе с ППП EXCEL и GRETL 1-й учебный вопрос. Практическая реализация косвенного МНК (КМНК)
Сведения из теории Экономика развивается в условиях эффектов прямой и обратной взаимозависимости и взаимной причинности. Например, численность населения и предложение продуктов питания – переменные, связанные взаимной причинностью. Такой эффект алгебраически описывается следующим образом:
Система эконометрических уравнений (CЭУ) вида (1.1), (1.2) может описывать, например, зависимость Y1t – спроса на птицу, Y2t – цены на птицу от X1t – дохода потребителей, X2t – цены на товар заменитель (говядину) и X3t – цены на корм птицы. Тогда первое уравнение системы (1.1) отражает поведение потребителей, а второе (1.2) – поставщиков птицы. Система (1.1), (1.2) относится к структурным СЭУ, поскольку результирующая переменная первого уравнения является объясняющей второго и наоборот. Структурная форма СЭУ непосредственно неприменима для решения задач оценивания и прогнозирования, так как уравнения системы не разрешены относительно эндогенных переменных. Поэтому осуществляют преобразование структурной формы СЭУ в приведенную форму, в которой правые части уравнений не содержат эндогенных переменных. Осуществим такое преобразование на примере системы (1.1, 1.2). Вначале, подставив вместо
Тогда, разрешив уравнение относительно
Выполним аналогичные преобразования для уравнения (1.2) и, разрешая его относительно
В общепринятом в литературе виде приведенная форма СЭУ для (1.1, 1.2) записывается так:
Здесь уже справедливо гипотеза о независимости шоковой vjt и экзогенных переменных, и для оценивания мультипликаторов можно применить МНК, который носит название косвенного МНК, так как строит оценки для π, по которым надо еще пересчитать оценки a и b. Например, для рассмотренного примера:
На практике для СЭУ преобразование в приведенную форму алгебраически не всегда возможно. Поэтом для уяснения ситуации применяют порядковый критерий проверки каждого уравнения СЭУ на идентифицируемость. Порядковый критерий (ПК) является необходимым, но недостаточным условием идентификации СЭУ, для его формулировки необходимо ввести: mi – число предопределенных переменных в i - ом уравнении, m – общее число предопределенных переменных в СЭУ (экзогенных и лаговых эндогенных); ni – число эндогенных переменных СЭУ в её i -ом уравнении. Порядковый критерий: Если число предопределенных переменных СЭУ, не включенных в i -ое уравнение не меньше, чем число эндогенных переменных СЭУ, содержащихся в анализируемом уравнении, уменьшенное на единицу, то данное уравнение считают идентифицируемым. Различают: а) точную идентификацию, если б) сверхидентификацию, если в) неидентифицируемость, если Задание 1 По системе совместных уравнений
в которой y 1 и y 2 - эндогенные переменные, x 2 – экзогенная переменная, а x 1 t =1, t =1,2,...,5, собраны следующие данные наблюдений над переменными модели:
1) Представьте систему в матричном виде и проведите проверку идентифицируемости каждого уравнения по порядковому критерию. 2) Запишите в явном матричном виде приведенную форму исходной системы (6.10.1), (6.10.2). 3) Оцените (косвенным МНК) параметры уравнения (6.10.1). 4) Пусть априорно известно, что 5) Используйте двухшаговый МНК для оценивания параметра
Показатели экономических процессов как случайные величины (ПЗ-1 (упражнение) – 2 часа) Учебные цели: 1. Проверить уровень знаний по основам математической статистики, изученным в ходе предшествующей подготовки и материала, доведенного на лекциях. 2. Учить порядку обработки результатов статистического наблюдения за показателями экономических процессов.
Учебные вопросы: 1. Выборочный метод в экономике. 2. Проверка нормальности распределения выборочных данных. Время проведения: 2 часа. Место проведения и учебно-материальное обеспечение: компьютерный класс со стандартным матобеспечением. Метод проведения: упражнение.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 412; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.91.245 (0.017 с.) |

 =118,2, n = 16, sX =3,6 и при уровне значимости α = 5% проверить:
=118,2, n = 16, sX =3,6 и при уровне значимости α = 5% проверить: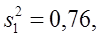


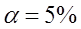 проверить H 0:
проверить H 0: 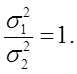
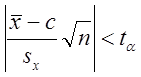
 ,
,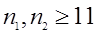 и
и  .
.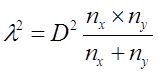 .
.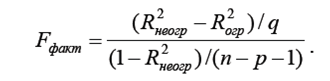

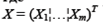 - вектор предопределенных (экзогенных и лаговых эндогенных) переменных;
- вектор предопределенных (экзогенных и лаговых эндогенных) переменных;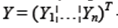 - вектор эндогенных переменных;
- вектор эндогенных переменных; - матрица коэффициентов, в которой bij - коэффициент при переменной yi в i -ом уравнении;
- матрица коэффициентов, в которой bij - коэффициент при переменной yi в i -ом уравнении;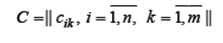 - матрица коэффициентов при переменной xk, в которой cik - коэффициент при переменной
- матрица коэффициентов при переменной xk, в которой cik - коэффициент при переменной 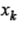 в i - ом уравнении;
в i - ом уравнении; - нулевой вектор.
- нулевой вектор. , тогда:
, тогда:
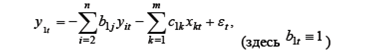
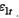
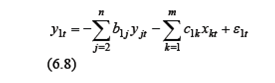
 эндогенных переменных
эндогенных переменных 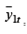 , на переменные, входящие в правую часть уравнения (6.8), и находим МНК-оценки
, на переменные, входящие в правую часть уравнения (6.8), и находим МНК-оценки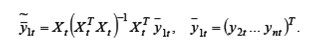
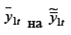 в уравнении (6.8):
в уравнении (6.8):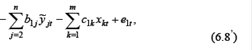
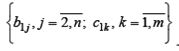
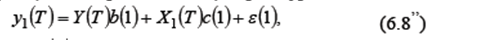
 - вектор наблюдений за эндогенной переменной, подлежащей определению в данном уравнении
- вектор наблюдений за эндогенной переменной, подлежащей определению в данном уравнении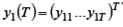
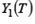 - матрица наблюдений над эндогенными переменными, объясняющими поведение y 1:
- матрица наблюдений над эндогенными переменными, объясняющими поведение y 1: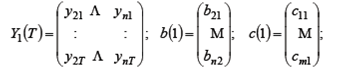
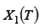 - матрица наблюдений за экзогенными переменными первого уравнения. Предполагается, что избранное уравнение для обеспечения состоятельности оценок идентифицируемо по порядковому критерию: «Для того чтобы уравнение модели было идентифицируемо, необходимо, чтобы число предопределенных переменных, не входящих в уравнение, было не меньше «числа эндогенных переменных, входящих в уравнение минус 1»
- матрица наблюдений за экзогенными переменными первого уравнения. Предполагается, что избранное уравнение для обеспечения состоятельности оценок идентифицируемо по порядковому критерию: «Для того чтобы уравнение модели было идентифицируемо, необходимо, чтобы число предопределенных переменных, не входящих в уравнение, было не меньше «числа эндогенных переменных, входящих в уравнение минус 1»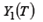 на оценку
на оценку 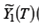 проведем следующие преобразования:
проведем следующие преобразования:
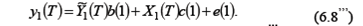




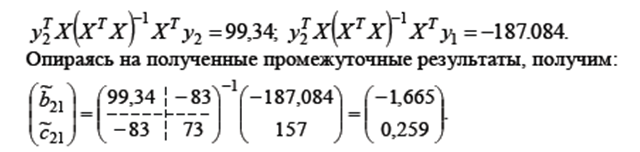
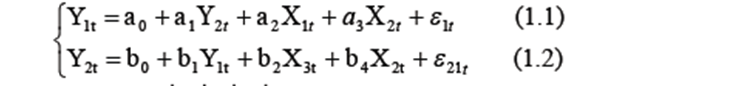
 его выражение из уравнения (1.2), получим:
его выражение из уравнения (1.2), получим: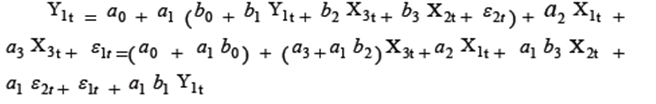
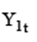 , получим:
, получим: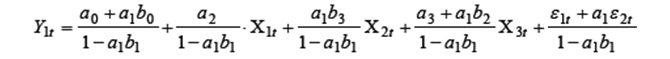
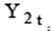 , будем иметь:
, будем иметь: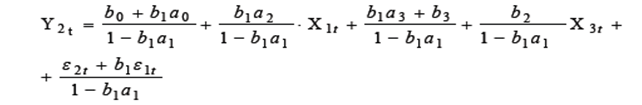
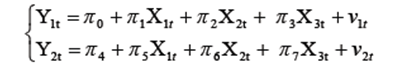


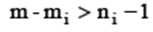 ;
;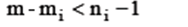 .
.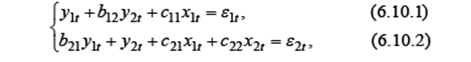

 . Как изменится вывод об идентифицируемости этого уравнения?
. Как изменится вывод об идентифицируемости этого уравнения? первого уравнения системы.
первого уравнения системы.


