
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Эконометрическое прогнозирование. Обнаружение и корректировка ошибок спецификацииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Учебные цели: 1. Совершенствовать навыки корреляционного анализа экономических процессов. 2. Изучить порядок моделирования взаимосвязей экономических показателей. Время проведения: 2 часа. Место проведения и учебно-материальное обеспечение: компьютерный класс со стандартным матобеспечением. Указания на подготовку: а) изучить учебный материал по конспекту лекций и рекомендуемой литературе; б) подготовиться к работе с ППП EXCEL 1-й учебный вопрос. Проверка выполнения предпосылок метода наименьших квадратов в множественной регрессии.
Сведения из теории Если один из столбцов матрицы Х уравнения регрессии может быть получен каклинейная комбинация остальных столбцов, то говорят, что имеет место полная коллинеарность. В этом случае определитель информационной матрицы (Х т Х) =0 и систему нормальных уравнений решить невозможно. Например, мы пытаемся получить зависимость потребления С от зарплаты S, дохода вне работы N и полного дохода Т:
Однако Т=S+N, т.е. переменные T и S или T и N взаимосвязаны. В результате мультиколлинеарность приводит к резкому снижению точности МНК–оценок коэффициентов регрессии. Операция их оценки становится неустойчивой (некорректной). Для оценки мультиколлинеарности факторов можно использовать определитель матрицы парных коэффициентов корреляции между факторами. Если факторы не коррелированы между собой, то корреляционная матрица факторов диагональна и ее определитель det R равен 1. Следовательно, чем ближе значение определителя корреляционной матрицы факторов к нулю, тем сильнее мультиколлинеарность и ненадежнее результаты регрессионного анализа. Наоборот, чем ближе det R к единице, тем меньше мультиколлинеарность. Гипотезу Н0: det R = 1 можно проверить, используя статистику
которая имеет распределение χ2 с n(n-1)/2 степенями свободы. Если расчетное значение данного критерия превосходит табличное значение, то Н0 отклоняется и факторы считаются мультиколлинеарными. Классический регрессионный анализ предполагает, что дисперсия аддитивных ошибок измерения постоянна, т.е. все наблюдения зависимой переменной имеют одну и ту же постоянную дисперсию ошибки наблюдения (такая модель называется гомоскедастичной). Если же дисперсия ошибок измерения для разных значений зависимой переменной непостоянна, такую модель называют гетероскедастичной, т.е. моделью с неодинаковым разбросом ошибок. Для идентификации таких моделей используется метод взвешенных наименьших квадратов. Оценки коэффициентов регрессии при использовании метода взвешенных наименьших квадратов (МНВК) находятся из условия.
Тесты на гетероскедастичность используют предположение о зависимости дисперсии ошибок измерения При использовании критерия Голдфельда-Квандта осуществляются следующие действия. 1. Все наблюдения в выборке упорядочиваются по убыванию величины регрессора хi, относительно которого есть подозрение на гетероскедастичность. 2. Из упорядоченного массива данных исключаются средних 3. Независимо друг от друга находятся уравнения регрессии для первых и последних 4. Находятся остаточные суммы квадратов для первой 5. Для проверки гипотезы о равенстве дисперсий, как всегда, используется F – критерий. Условие принятия гипотезы о равенстве дисперсий (т.е. отсутствие гетероскедастичности):
(p – число коэффициентов в уравнении регрессии).
Задание 1. В табл. 6.1 приведены данные о спросе (y) и цене (x 1) на новый товар, данные о ценах на товары-заместители (x 2, x 3) и среднем доходе домохозяйств (x 4). Таблица 6.1
Требуется: 1) построить уравнение множественной линейной регрессии, оценить его адекватность и дать экономическую интерпретацию коэффициентам уравнения; 2) оценить стандартную ошибку регрессии и стандартные ошибки коэффициентов; 3) сделать выводы по качеству построенной модели.
Задание 2. Используя результаты выполнения задания 1: а) протестируйте модель на мультиколлинеарность факторов и, при существовании таковой, примите меры к ее устранению; б) вновь построенную модель проверьте на гетероскедастичность и, в случае ее наличия, осуществите преобразование, позволяющее снизить ее влияние на адекватность регрессионного уравнения. Получите оценки качества новой модели; в) по наиболее адекватной модели выполните прогноз спроса на новый товар в периоде с номером 16.
Задание 3. Используя данные задания 1, проверьте гипотезу о наличии автокорреляции по переменным задачи. Указание к решению. Для проверки нулевой гипотезы используют статистику Дарбина-Уотсона, рассчитываемую по формуле:
2-й учебный вопрос. Корректировка ошибок спецификации в множественной регрессии. Задание 4. Обычным МНК по данным наблюдений за 150 жителями страны получена зависимость между доходом индивидуума у, его уровнем образования х1, принимающем значения от 1 до 5, и возрастом х2:
Далее по упорядоченным значениям переменной х 2 и остатков моделиустановлено, что
Проверьте гипотезу о наличии гетероскедастичности в данных о возрасте аборигенов. Затем, на основе введения вспомогательных переменных
полагая, что для уровня значимости 0,05 при числе степеней свободы f ≥ 49 квантиль распределения Стьюдента tкр= 3, а стандартные ошибки коэффициентов
Задание на самостоятельную работу: 1. Допуская, что дисперсия ошибки коррелирует с переменной H2 , проверьте по данным табл.1 гипотезу о наличии гетероскедастичности в модели G=a0+a1H1+a2H2+e. Таблица 1
2. По данным табл. 2 проверьте модель Y=a0+a1X1+a2X2+a3X3+e на наличие автокорреляции при критических значениях статистики Дарбина-Уотсона dl =1.45 и du =1.78. Таблица 2
3. Студентом журфака, продвинутым «параллельным» бакалавриантом экономфака, построена эконометрическая модель, объясняющая годовой тираж региональных газет с коэффициентом детерминации в 0,69:
где Ci - годовой тираж i -ой газеты; Pi - средняя цена i -ой газеты в год; Ii - общий доход жителей региона, в котором распространялась i -ая газета; Qi - число персональных рубрик редактора в i -ой газете; Ai - размер цены (розничной) на рекламу, размещаемую в i -ой газете; Si - число конкурирующих изданий в регионе, где распространяется i -ая газета; Ti - число телевизионных каналов в регионе распространения i -ой газеты. В скобках приведены стандартные ошибки соответствующих коэффициентов.
Выполните: а) Проверьте правдоподобие знаков у коэффициентов модели и значимость ее параметров с надежностью 0,95. б) Оцените мультиколлинеарность факторов модели на основании имеющейся информации. К сведению: Наиболее часто применимы следующие критерии наличия мультиколлинеарности: 1) При высокой значимости всего уравнения (R 2), значимость индивидуальных экзогенных переменных мала. 2) Высокое значение коэффициента парной корреляции входящих в модель экзогенных переменных (r ≥ 0,8). в) Сформулируйте предложения по модификации модели, которые сделают ее более адекватной.
Занятие 7.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 716; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.011 с.) |


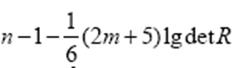 ,
,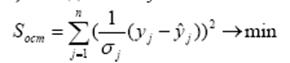
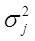 от значений регрессоров.
от значений регрессоров. значений.
значений.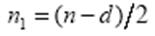 наблюдений.
наблюдений. и второй
и второй 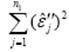 частей выборки. Если предположение относительно природы гетероскедастичности верно, то дисперсия остатков для первого уравнения регрессии должна быть больше, чем дисперсия остатков для второго уравнения регрессии.
частей выборки. Если предположение относительно природы гетероскедастичности верно, то дисперсия остатков для первого уравнения регрессии должна быть больше, чем дисперсия остатков для второго уравнения регрессии.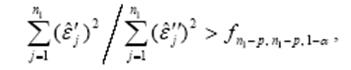
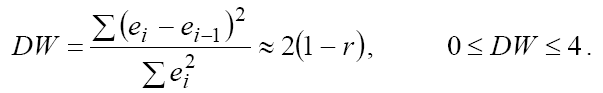
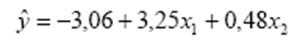
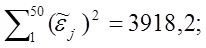
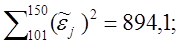
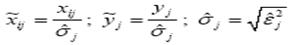 , достройте новое уравнение регрессии, получаемое взвешенным МНК
, достройте новое уравнение регрессии, получаемое взвешенным МНК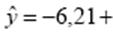

 ,
, .
.



