
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Отбор объясняющих переменных методом дополнительной регрессииСодержание книги
Поиск на нашем сайте
2 принципа такого отбора: - в модели следует оставлять только значащие факторы, используя при определении значащих факторов T-тест - при отборе фактора хj в модель строится для этого фактора дополнительная регрессия xjt=b0+b1x1,t+…+bj-1xj-1,t+bj+1xj+1,t+…+vj,t и вычисляется Rj2 в модели сохраняются те факторы, у которых коэффициенты детерминации в дополнительной регрессии наименьшие, а коэффициента корреляции стремятся к максимуму
57. Эконометрические модели в виде систем линейных одновременных уравнений (СЛОУ): примеры и проблема идентификации (на примере модели спроса-предложения блага). В общем случае экономическая модель может включать в себя несколько текущих эндогенных переменных. Линейная экономическая модель в общем случае имеет спецификацию Пример – модель спроса и предложения на конкурентном рынке: Модель (1) называют моделью из одновременных уравнений, поскольку какие-то эндогенные переменные модели в некоторых поведенческих уравнениях могут играть роль объясняющих переменных, например, в модели (2) объясняющей эндогенной переменной в обоих уравнениях является цена р. Моделям (1) присущи 2 проблемы – проблема идентификации и проблема оценивания параметров структурной формы. Рассмотрим первую проблему на примере модели (2). Можно ли определить параметры а0, а1, b0, b1 поведенческих уравнений? Построим графики спроса и предложения.
 и уровень спроса и предложения по равновесной цене и уровень спроса и предложения по равновесной цене  .Знание точки Е не позволяет определить ни параметры кривой спроса, ни предложения. .Знание точки Е не позволяет определить ни параметры кривой спроса, ни предложения.
Поясним эту мысль, составив приведенную форму (случайные остатки пока опустим)
Опр: Поведенческое уравнение модели (1) является идентифицируемым, если по известным коэффициентам приведенной формы модели можно определить коэффициенты данного поведенческого уравнения.
57. Эконометрические модели в виде систем линейных одновременных уравнений (СЛОУ): примеры и проблема оценивания параметров структурной формы (на примере макромодели Кейнса). В общем случае экономическая модель может включать в себя несколько текущих эндогенных переменных. Линейная экономическая модель в общем случае имеет спецификацию Пример – модель Кейнса Модель (1) называют моделью из одновременных уравнений, поскольку какие-то эндогенные переменные модели в некоторых поведенческих уравнениях могут играть роль объясняющих переменных, например, в модели (2) У объясняет С. Моделям (1) присущи 2 проблемы – проблема идентификации и проблема оценивания параметров структурной формы. Рассмотрим вторую проблему на примере модели Кейнса (2). Проблема состоит в зависимости (коррелированности) эндогенных объясняемых переменных и случайных остатков соответствующих поведенческих уравнений. Запишем приведенную форму модели (2): Рассматривая второе уравнение в (3), мы констатируем, что Y является линейной функцией случайного остатка u. По теории вероятности 59. Необходимое условие идентифицируемости поведенческого уравнения модели СЛОУ (правило порядка). Сверхидентифицируемость параметров поведенческого уравнения. Запишем исследуемое поведенческое уравнение модели СЛОУ в виде
Поведенческое уравнение в компактной записи: Теорема. Пусть поведенческое уравнение (1) идентифицируемо. Тогда справедливо неравенство Неравенство (2) позволяет определить неидентифицируемое уравнение, но не позволяет определить идентифицируемое. Такое определение может дать критерий (необходимое и достаточное условие). Если имеет место неравенство
60. Необходимое условие идентифицируемости поведенческого уравнения модели СЛОУ (правило порядка) Рассмотрим модель СЛОУ и запишем ее исследуемое поведенческое уравнение в следующем виде:
Здесь G – число текущих эндогенных (объясняемых) переменных модели; К – кол-во предопределенных переменных, в состав которых, возможно, входит 1. Например, в модели Кейнса: G =2, K=2.
Равенство Можем записать поведенческое уравнение компактнее:
Справедлива следующая теорема: Пусть поведенческое уравнение (1) идентифицируемо. Тогда справедливо следующее неравенство: Где Замечание: неравенство (2) позволяет определить неидентифицируемые поведенческие уравнения, но не позволяет определить идентифицируемые. Такое определение способен дать критерий идентифицируемости. Пример: простейшая модель спроса- предложения блага на конкурентном рынке. Рассмотрим первое поведенческое уравнение:
61. Критерий идентифицируемости поведенческого уравнения модели СЛОУ (правило ранга) Обратимся к записи исследуемого поведенческого уравнения модели
Компактная запись: Обычно вектор коэф-ов
|
|||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 430; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.255.196 (0.009 с.) |

 (1).
(1). (2)
(2)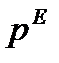


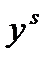
 (3). Рассматривая (3), констатируем, что эта форма состоит из двух уравнений с четырьмя искомыми параметрами. Определить их однозначно нельзя. В этом и заключается неидентифицируемость обоих уравнений модели (2). Например, если (3) разрешить относительно а1 и b1:
(3). Рассматривая (3), констатируем, что эта форма состоит из двух уравнений с четырьмя искомыми параметрами. Определить их однозначно нельзя. В этом и заключается неидентифицируемость обоих уравнений модели (2). Например, если (3) разрешить относительно а1 и b1: 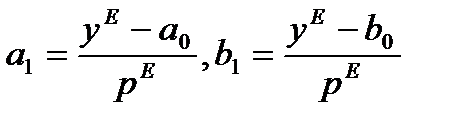 , то задаваясь любыми подходящими а0, b0 получим то или иное решение уравнений (3).
, то задаваясь любыми подходящими а0, b0 получим то или иное решение уравнений (3). (2)
(2) (3)
(3) , значение Y коррелирует со значением случайного остатка u. Следовательно, в силу наличия ненулевой ковариации в уравнениях наблюдений модели Кейнса оказывается нарушенной последняя предпосылка теоремы ГМ. Нарушение этой предпосылки порождает несостоятельность оценок параметров модели (1), вычисленных МНК, ВМНК или ОМНК.
, значение Y коррелирует со значением случайного остатка u. Следовательно, в силу наличия ненулевой ковариации в уравнениях наблюдений модели Кейнса оказывается нарушенной последняя предпосылка теоремы ГМ. Нарушение этой предпосылки порождает несостоятельность оценок параметров модели (1), вычисленных МНК, ВМНК или ОМНК.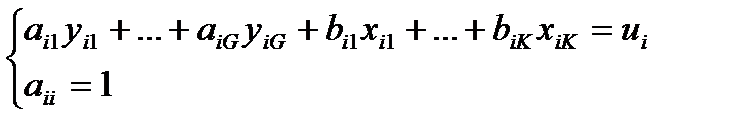 (1), где G – количество текущих эндогенных переменных, К – кол-во предопределенных переменных.
(1), где G – количество текущих эндогенных переменных, К – кол-во предопределенных переменных. - условие нормализации, оно означает, что в исследуемом поведенческом уравнении объясняемая эндогенная переменная выражена в явном виде через объясняющие переменные и, возможно, через другие эндогенные переменные.
- условие нормализации, оно означает, что в исследуемом поведенческом уравнении объясняемая эндогенная переменная выражена в явном виде через объясняющие переменные и, возможно, через другие эндогенные переменные. .
. (2), где Кi, — количество предопределенных переменных модели, входящих в i-е уравнение; Gi — количество эндогенных переменных модели, входящих в i-е уравнение модели.
(2), где Кi, — количество предопределенных переменных модели, входящих в i-е уравнение; Gi — количество эндогенных переменных модели, входящих в i-е уравнение модели. , то говорят о сверхидентифицируемости i-того уравнения модели. В этой ситуации количество уравнений в системе превышает количество ее неизвестной, то есть система является переопределенной и совместной.
, то говорят о сверхидентифицируемости i-того уравнения модели. В этой ситуации количество уравнений в системе превышает количество ее неизвестной, то есть система является переопределенной и совместной.

 называется условием нормализации, оно означает, что в исследуемом поведенческом уравнении объясняемая эндогенная переменная выражена в явном виде через объясняющие переменные и, возможно, какие-то другие эндогенные переменные. Например, в модели Кейнса в поведенческом уравнении эндогенная переменная
называется условием нормализации, оно означает, что в исследуемом поведенческом уравнении объясняемая эндогенная переменная выражена в явном виде через объясняющие переменные и, возможно, какие-то другие эндогенные переменные. Например, в модели Кейнса в поведенческом уравнении эндогенная переменная 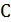 выражена в явном виде (является явной функцией от переменных Y(эндогенной) и 1).
выражена в явном виде (является явной функцией от переменных Y(эндогенной) и 1). , где
, где 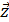 - вектор переменных модели: эндогенных и экзогенных;
- вектор переменных модели: эндогенных и экзогенных;  - коэф. при объясняемых и объясняющих переменных.
- коэф. при объясняемых и объясняющих переменных. (2)
(2) число объясняющих переменных, входящих в данное исследуемое поведенческое уравнение.
число объясняющих переменных, входящих в данное исследуемое поведенческое уравнение. 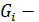 кол-во эндогенных переменных входящих в исследуемое поведенческое уравнение.
кол-во эндогенных переменных входящих в исследуемое поведенческое уравнение.

 , где
, где 
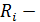 горизонтальная прямоугольная матрица, кол-во строк которой совпадает с числом априорно нулевых коэффициентов. С позиции линейной алгебры ограничения (1) на параметры повед.ур-я являются системой линейных однородных ур-ний.
горизонтальная прямоугольная матрица, кол-во строк которой совпадает с числом априорно нулевых коэффициентов. С позиции линейной алгебры ограничения (1) на параметры повед.ур-я являются системой линейных однородных ур-ний.


