
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Критерий (необходимое и достаточное условие) идентифицируемости поведенческого уравнения.Содержание книги
Поиск на нашем сайте
Пусть символом Пример: м-ль Кейнса.
Матрица коэф-ов компактной записи структурной формы данной модели имеет вид: Следовательно, критерий идентифицируемости выполняется, и,значит, повед.ур-е данной модели идентифицируемо.
62. Понятие инструментальных переменных. Оценивание параметров структурной формы двухшаговым м-ом наименьших квадратов на примере простейшей макромодели Кейнса 2МНК – двухшаговый метод наименьших квадратов – наиболее удобный для расчетов метод состоятельного оценивания коэф-ов идентифицируемых поведенческих ур-ний. Алгоритм 2МНК обсудим на примере оценивания м-ли Кейнса: 1 шаг. Оценить МНК параметры приведенной формы м-ли для эндогенных переменных Для м-ли Кейнса уравнения наблюдений:
2 шаг. Вычислить прогнозн.значения
3 шаг. Оценить МНК структурные параметры поведенч.ур-я, рассматривая оценки Для м-ли Кейнса уравнен.наблюдений на 2-ом шаге имеют вид:
Полученные МНК по этим уравнениям оценки Упомянутые в алгоритме 2МНК прогнозные значения эндогенных переменных служат примером инструментальных переменных, которые экономисты используют для вычисления состоятельных оценок коэф-ов повед.ур-ний в ситуации нарушения последней предпосылки теоремы Гаусса-Маркова. Определение: Пусть объясняющие переменные в ЛММР коррелируют в пределе со случайным остатком 1. в пределе не коррелируются случайным остатком модели 2. матрица Тогда оценки модели ЛММР, вычисленные по правилу
63. Теорема Слуцкого и оценивание параметров структурной формы косвенным методом наименьших квадратов (КМНК) – на примере простейшей макромодели Кейнса. Рассмотрим структурную форму модели СЛОУ и трансформируем ее к приведенной форме, т.е. выразим вектор Добавим, что матрица М может быть оценена по результатам наблюдений эндогенных и предопределенных переменных данной модели, например, методом наим.кв-ов. Теорема Слуцкого Пусть
Запишем с учетом отмеченного выражения матрицы Рассматривая эту систему, констатируем, что искомый вектор коэф-ов Согласно теореме Слуцкого, оценка вектора КМНК для м-ли Кейнса 1. Структурная форма 2. Приведенная форма
Пусть в результате оценивания МНК приведенной формы модели получились оценки параметров
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 302; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.211.190 (0.007 с.) |

 обозначена матрица коэф-ов компактного вида
обозначена матрица коэф-ов компактного вида обозначена матрица линейных ограничений на параметры исследуемого пов.ур-я. Это уравнение идентифицируемо т.и т.т.,к. справедливо рав-во:
обозначена матрица линейных ограничений на параметры исследуемого пов.ур-я. Это уравнение идентифицируемо т.и т.т.,к. справедливо рав-во:  .
.  ранг матрицы,
ранг матрицы,  тек.эндог.переменные м-ли.
тек.эндог.переменные м-ли.
 век-р эндогенных переменных
век-р эндогенных переменных 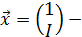 в-р экзогенных переменных. Из векторов
в-р экзогенных переменных. Из векторов  собираем
собираем 


 , включенных в правую часть оцениваемого поведенческого уравнения.
, включенных в правую часть оцениваемого поведенческого уравнения.
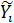 по оцененной приведенной форме модели. Для модели Кейнса формула расчета прогнозных значений выглядит так:
по оцененной приведенной форме модели. Для модели Кейнса формула расчета прогнозных значений выглядит так: оптимальное прогнозное значение дохода
оптимальное прогнозное значение дохода как значения объясняющих переменных.
как значения объясняющих переменных.
 являются состоятельными оценками коэф-ов (
являются состоятельными оценками коэф-ов ( и носят название оценок структурных параметров двухшаговым мет-ом наим.кв-ов (2МНК).
и носят название оценок структурных параметров двухшаговым мет-ом наим.кв-ов (2МНК).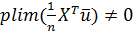 , т.е. нарушена последняя предпос.т.Гаусса-Маркова. Переменные
, т.е. нарушена последняя предпос.т.Гаусса-Маркова. Переменные  инструментальные, если они удовлетворяют 2 требованиям:
инструментальные, если они удовлетворяют 2 требованиям:
 невырожденная
невырожденная являются состоятельными.
являются состоятельными. через вектор
через вектор  Символом
Символом  обозначим матрицу коэффициентов приведенной формы модели.Эта матрица следующим образом зависит от
обозначим матрицу коэффициентов приведенной формы модели.Эта матрица следующим образом зависит от  и
и  (
( )
)  .
. матрица состоятельных МНК-оценок коэф-ов приведенной формы модели СЛОУ, т.е.
матрица состоятельных МНК-оценок коэф-ов приведенной формы модели СЛОУ, т.е.  . Пусть
. Пусть  любая рациональная вектор-функция, такая что значение
любая рациональная вектор-функция, такая что значение  конечно. Тогда
конечно. Тогда  .
.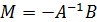 , линейного ограничения на параметры
, линейного ограничения на параметры  и условия нормализации
и условия нормализации  систему уравнений, которой удовлетворяет вектор искомых параметров
систему уравнений, которой удовлетворяет вектор искомых параметров  исследуемого поведенческого уравнения
исследуемого поведенческого уравнения  I- единичная матрицца
I- единичная матрицца рациональная функция матрицы
рациональная функция матрицы 
 , вычисленная в процессе решения системы (1)
, вычисленная в процессе решения системы (1)  оказывается состоятельной оценкой вектора
оказывается состоятельной оценкой вектора 
 - оценки поведенческого уравнения косвенным методом наименьших квадратов.
- оценки поведенческого уравнения косвенным методом наименьших квадратов.
 и
и  (
( . Подставляя эти оценки в наше уравнение и разрешая эти уравнения относительно
. Подставляя эти оценки в наше уравнение и разрешая эти уравнения относительно  и
и  , получим оценки косвенным м-ом наименьших квадратов, т.е.
, получим оценки косвенным м-ом наименьших квадратов, т.е.  и
и  .
.


