
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классификация кривых второго порядкаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Невырожденные кривые Кривая второго порядка называется невырожденной, если
Вырожденные кривые Кривая второго порядка называется вырожденной, если Δ = 0. Могут возникать следующие варианты:
Диаметры и центр кривой второго порядка Диаметром кривой второго порядка называется геометрическое место середин параллельных хорд этой кривой. Полученный таким образом диаметр называется сопряжённым этим хордам или их направлению. Диаметр, сопряжённый хордам, образующих угол θ с положительным направлением оси Ox, определяется уравнением:
Если выполняется условие Координаты центра
Решая эту систему относительно x 0 и y 0, получим:
Если кривая центральная, то перенос начала координат в её центр приводит уравнение к виду
где Главные оси и вершины кривой второго порядка Главной осью кривой второго порядка называется её диаметр, перпендикулярный к сопряжённым к ним хордам. Этот диаметр является осью симметрии кривой. Каждая центральная кривая Направляющие косинусы нормалей к главным осям удовлетворяют уравнениям
где λ — отличный от нуля корень характеристического уравнения. Направления главных осей и сопряжённых им хорд называются главными направлениями кривой. Угол между положительным направлением оси Ox и каждым из двух главных направлений определяется формулой
Из всех видов кривых второго порядка только окружность имеет неопределённые главные направления. Уравнения Общее уравнение в матричном виде Общее уравнение кривой можно записать в матричном виде
Канонический вид Вводом новой системы координат можно привести уравнения кривых второго порядка к стандартному каноническому виду (см. таблицу). Параметры канонических уравнений весьма просто выражаются через инварианты
Для центральной кривой в каноническом виде её центр Через эксцентриситет Каноническое уравнение любой невырожденной кривой второго порядка при помощи подходящего преобразования начала координат может быть приведено к виду
В этом случае кривая проходит через начало новой системы координат, а ось Ox является осью симметрии кривой. Данное уравнение выражает тот факт, что невырожденная кривая второго порядка является геометрическим местом точек, отношение расстояний которых Уравнение директрисы кривой выражается уравнением Если кривая второго порядка центральная (эллипс или гипербола), то прямая
является осью симметрии и, следовательно, кривая имеет два фокуса и две директрисы. Параметр p называется фокальным параметром и равен половине длины хорды, проходящей через фокус и перпендикулярной к фокальной оси (фокальная хорда). Полярные координаты Если взять в качестве полюса полярной системы координат
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 2347; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

 Могут возникать следующие варианты:
Могут возникать следующие варианты:

 то все диаметры кривой пересекаются в одной точке — центре, а сама кривая называется центральной. В противном случае (D = 0) все диаметры кривой либо параллельны, либо совпадают.
то все диаметры кривой пересекаются в одной точке — центре, а сама кривая называется центральной. В противном случае (D = 0) все диаметры кривой либо параллельны, либо совпадают. определяются системой уравнений:
определяются системой уравнений:


 — координаты относительно новой системы.
— координаты относительно новой системы.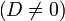 либо имеет две взаимно перпендикулярные оси, либо все диаметры являются главными осями. В последнем случае кривая является окружностью. Нецентральные кривые
либо имеет две взаимно перпендикулярные оси, либо все диаметры являются главными осями. В последнем случае кривая является окружностью. Нецентральные кривые  имеют лишь одну главную ось. Точки пересечения главной оси с самой кривой называются её вершинами.
имеют лишь одну главную ось. Точки пересечения главной оси с самой кривой называются её вершинами.


 и корни характеристического уравнения
и корни характеристического уравнения  (см. выше раздел «Характеристическая квадратичная форма и характеристическое уравнение»).
(см. выше раздел «Характеристическая квадратичная форма и характеристическое уравнение»).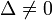 )
)













 (эксцентриситет) от данной точки (фокуса) и от данной прямой (директрисы) постоянно. Кроме того, при
(эксцентриситет) от данной точки (фокуса) и от данной прямой (директрисы) постоянно. Кроме того, при  кривая является окружностью, при
кривая является окружностью, при  — эллипсом, при
— эллипсом, при  — параболой, при
— параболой, при  — гиперболой.
— гиперболой. а координаты фокуса
а координаты фокуса  Директриса перпендикулярна оси симметрии, проходящей через фокус и вершину кривой (фокальная ось). Расстояние между фокусом и директрисой равно
Директриса перпендикулярна оси симметрии, проходящей через фокус и вершину кривой (фокальная ось). Расстояние между фокусом и директрисой равно 

 фокус невырожденной кривой второго порядка, а в качестве полярной оси — её ось симметрии, то в полярных координатах ρ, φ уравнение кривой будет иметь вид
фокус невырожденной кривой второго порядка, а в качестве полярной оси — её ось симметрии, то в полярных координатах ρ, φ уравнение кривой будет иметь вид



