
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства транспонированных матрицСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Свойства транспонированных матриц
.
2. Определители и их свойства .Определитель матрицы является многочленом от элементов квадратной матрицы (то есть такой, у которой количество строк и столбцов равны)
Меняя столбцы или строки местами, величина определителя не меняется. Перестановив строки или столбцы местами определитель умножается на -1. Если есть нулевая строка(столбец) то определитель равен нулю Раевн нулю если есть пропорциональные или равные строки Если к элементам одной строки(столбца) прибавить элементы другого столбца(строки) То величина определителя не изменится.
3. Определение минора и алгебраического дополнения данного элемента матрицы. Две теоремы связанные с понятием алгебраического дополнения Минором элемента
Алгебраическим дополнением элемента Обозначение: Теорема (о разложении определителя по заданной строке или столбцу). Определитель равен сумме произведений элементов какой–либо его строки (или столбца) на их алгебраические дополнения.
4. Понятие обратной матрицы теорема о существовании обратной матрицы .Понятие обратной матрицы вводится только для квадратных матриц. Если A – квадратная матрица, то обратной для неё матрицей называется матрица, обозначаемая A-1 и удовлетворяющая условию Справедлива следующая теорема: Теорема. Для того чтобы квадратная матрица A имела обратную, необходимо и достаточно, чтобы её определитель был отличен от нуля.
5. Решение матричных уравнений с помощью обратной матрицы. Решение систем линейных алгебраических уравнений с невырожденной матрицей. Метод Крамера.
5.Матричные уравнения могут иметь вид: АХ = В, ХА = В, АХВ = С, где А,В,С — задаваемые матрицы, Х- искомая матрица. Матричные уравнения решаются с помощью умножения уравнения на обратные матрицы. Например, чтобы найти матрицу Х из уравнения АХ = В, необходимо умножить это уравнение на А-1 слева и справа. Тогда: Описание метода(краммер) Для системы n линейных уравнений с n неизвестными (над произвольным полем)
с определителем матрицы системы Δ, отличным от нуля, решение записывается в виде
(i-ый столбец матрицы системы заменяется столбцом свободных членов).
6. Метод Гаусса. Теорема о наличии ненулевого решения однородной системы линейных алгебраических уравнений с прямоугольной матрицей А(mxn) при n>m. Ме́тодГа́усса [1] — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные Рангом системы строк (столбцов) матрицы A с m строк и n столбцов называется максимальное число линейно независимых строк (столбцов). Несколько строк (столбцов) называются линейно независимыми, если ни одна из них не выражается линейно через другие. Ранг системы строк всегда равен рангу системы столбцов, и это число называется рангом матрицы.
Если ранг меньше числа строк то система имеет свободные переменные и бесконечное число решений. Если арнг равен строкам то есть одно решение. Когда n>m то есть число неизвестных больше то решений очень много. Пример Решим систему Перепишем её в матричном виде:
Путём элементарных преобразований над строками приведём её основную матрицу к ступенчатому виду:
Таким образом ранг системы (ранг её основной матрицы) равен двум. Это значит, что существует Перепишем полученную систему в виде уравнений:
Возьмём
Подставим по очереди единицы в качестве одной из свободных переменных:
Тогда общее решение рассматриваемой системы может быть записано так:
а вектора
12. Структура решения неоднородной системы линейных алгебраических уравнений.
Неоднородной системой линейных уравнений называется система вида:
§ если § если Пример Решим систему Преобразуем её к Тогда переменные Заметим, что Составим однородную систему: Тогда, подставив единицу в качестве свободной переменной
Общее решение системы может быть записано так:
13. Теорема о связи ранга квадратной матрицы и ее определителя. Решение однородной и неоднородной систем уравнений с квадратной матрицей. Пусть
14. Понятие геометрического вектора. Линейные операции над векторами. Невырожденные кривые Кривая второго порядка называется невырожденной, если
Вырожденные кривые Кривая второго порядка называется вырожденной, если Δ = 0. Могут возникать следующие варианты:
Уравнения Канонический вид Вводом новой системы координат можно привести уравнения кривых второго порядка к стандартному каноническому виду (см. таблицу). Параметры канонических уравнений весьма просто выражаются через инварианты
Для центральной кривой в каноническом виде её центр Через эксцентриситет Каноническое уравнение любой невырожденной кривой второго порядка при помощи подходящего преобразования начала координат может быть приведено к виду
В этом случае кривая проходит через начало новой системы координат, а ось Ox является осью симметрии кривой. Данное уравнение выражает тот факт, что невырожденная кривая второго порядка является геометрическим местом точек, отношение расстояний которых Уравнение директрисы кривой выражается уравнением Если кривая второго порядка центральная (эллипс или гипербола), то прямая
является осью симметрии и, следовательно, кривая имеет два фокуса и две директрисы. Параметр p называется фокальным параметром и равен половине длины хорды, проходящей через фокус и перпендикулярной к фокальной оси (фокальная хорда). Полярные координаты Если взять в качестве полюса полярной системы координат
Касательные и нормали Уравнение касательной к кривой второго порядка f (x, y) в её точке
Уравнение нормали к кривой второго порядка в точке
Полюсы и поляры Уравнение
помимо касательной опряделяет прямую, называемую полярой точки Теоремы о полюсах и полярах:
Из этих утверждений, в частности, следует, что:
26. Общее уравнение плоскости Общее уравнение плоскости
Определение. Плоскостью называется поверхность, все точки которой удовлетворяют общему уравнению: Ax + By + Cz + D = 0 где А, В, С – координаты вектора
Возможны следующие частные случаи: А = 0 – плоскость параллельна оси Ох В = 0 – плоскость параллельна оси Оу С = 0 – плоскость параллельна оси Оz D = 0 – плоскость проходит через начало координат А = В = 0 – плоскость параллельна плоскости хОу А = С = 0 – плоскость параллельна плоскости хОz В = С = 0 – плоскость параллельна плоскости yOz А = D = 0 – плоскость проходит через ось Ох В = D = 0 – плоскость проходит через ось Оу С = D = 0 – плоскость проходит через ось Oz А = В = D = 0 – плоскость совпадает с плоскостью хОу А = С = D = 0 – плоскость совпадает с плоскостью xOz В = С = D = 0 – плоскость совпадает с плоскостью yOz
27. Неполные уравнения плоскости. Уравнение плоскости в отрезках. Угол между двумя прямыми
Плоскость 1) пересекаются 2) прямая лежит в плоскости 3) параллельны Если 1) 2) 3)
37. Точка пересечения прямой и плоскости. Определение точки пересечения прямой и плоскости Будем считать, что плоскость
38. Уравнение плоскости, проходящей через точку и прямую.
Берём 2 точки на прямой затем
уравнение плоскости, проходящей через три точки:
39. Расстояние от точки до прямой (в пространстве) Расстояние точки A (x 1, y 1) до прямой Ax + By + C = 0 есть длина перпендикуляра, опущенного из этой точки на прямую. Она определяется по формуле
Правило. Чтобы определить расстояние точки A (x 1, y 1) до прямой Ax + By + C = 0, нужно привести уравнение прямой к нормальному виду, взять левую часть полученного уравнения и подставить в нее вместо текущих координат координаты данной точки. Абсолютная величина полученного числа и даст искомое расстояние:
Расстояние от точки до прямой есть всегда величина положительная. Кроме расстояния от точки до прямой, рассматривается еще так называемое отклонение точки от прямой. Отклонение Расстояние от точки до прямой есть абсолютная величина отклонения этой точки от прямой.
40. Расстояние между скрещивающимися прямыми. Определение Линейное, или векторное пространство 1. сложения, то есть каждой паре элементов множества 2. умножения на скаляр (то есть элемент поля P), то есть любому элементу При этом на операции накладываются следующие условия: 1. 2. 3. существует такой элемент 4. для любого 5. 6. 7. 8. Элементы множества L называют векторами, а элементы поля P — скалярами. Свойства 1-4 совпадают с аксиомами абелевой группы. Простейшие свойства 1. Векторное пространство является абелевой группой по сложению. 2. Нейтральный элемент 3. 4. Для любого 5. 6. 7.
43. Определение базиса линейного пространства. Теорема о единственности разложения вектора по данному базису. Базис - любая упорядоченная система Обозначение: Для каждого вектора
Числа
Теорема. (О разложении вектора по базису.) Любой вектор векторного пространства можно разложить по его базису и притом единственным способом. Доказательство. 1) Пусть L произвольная прямая (или ось) и
44. Координаты вектора линейного пространства в данном базисе. Способ определения линейно зависимости векторов линейного пространства. . Пусть e1,e2,…,en – базис пространства V, x,y – произвольные элементы пространства V. При сложении элементов их координаты складываются, при умножении произвольного элемента х на любое число l все координаты этого элемента умножаются на l. [Док-во]: x=a1e1+a2e2+…+anen=i=1ånaiei=(e1,e2,…,en)(a1,a2,…,an). y=b1e1+b2e2+…+bnen=i=1ånbiei=(e1,e2,…,en)(b1,b2,…,bn). 1) x+y= i=1ånaiei+i=1ånbiei=i=1ån(aI+bI)ei=(e1,e2,…,en)(a1+b1,…,an+bn)= (a1+b1)e1+…+(an+bn)en; 2) lx=l* i=1ånaiei= i=1ånlaiei=(e1,e2,…,en)(la1,…,lan)= (la1)e1+…+(lan)en [Лемма]: Пусть e1,e2,…,en базис в пространстве V, f1, f2,…, fn – элементы пространства V. Векторы f1, f2,…, fn линейно зависимы в том и только том случае, когда линейно зависимы столбы их координат. [Док-во]: f1= (e1,e2,…,en)(a1,a2,…,an) l1f1+l2f2+…+lnfn=(e1,e2,…,en)[l1(a11,a12,…,a1n)+…+ln(an1,an2,…,ann)] => вектора f1,f2,…,fnлинейно зависимы в том и только том случае, когда l1(a11,a12,…,a1n)+…+ln(an1,an2,…,ann) = (0,0,…,0) а это значит, что столбцы их координат должны быть линейно зависимыми. Система векторов e 1, e 2,..., e k линейного пространства L называется линейно независимой системой, если равенство С1· e 1+С2 ·e 2+...+Сk · e k = 0 возможно только когда все коэффициенты С1, С2,..., Сk равны нулю. Здесь 0 — нулевой вектор линейного пространства L, С1, С2,..., Сk — числовые коэффициенты. Если система векторов e 1, e 2,..., e k линейного пространства L не является линейно независимой системой, то она называется линейно зависимой системой векторов.
45. Связь между базисами линейного пространства. Матрица перехода (теорема о невырожденной матрицы перехода) Матрица перехода Ма́трицейперехо́да от базиса Обозначается . Так как
Матрица перехода это
46. Преобразование координаты вектора при замене базиса. . Пусть системы векторов e = {e 1,..., e n } и f = {f 1,..., f n } — два базиса n -мерного линейного пространства Ln. Обозначим xe = (x 1, x 2,..., x n) и xf = (x' 1, x' 2,..., x' n) — координаты вектора x ∈ Ln соответственно в базисах e и f. Справедливо следующее xe = Ce→f·xf:
Здесь Ce→f — матрица перехода от базиса e к базису f, это матрица, столбцами которой являются координаты базисных векторов f1,..., f n в базисе e 1,..., e n: f1 = с 11· e2 + с 21 ·e1+... + с n 1 ·e n, f2 = с 12· e1 + с 22 ·e2+... + с n 2 ·e n, ..., f n = с 1 n · e2 +... + с nn ·e n. Формулу преобразования координат вектора при изменении базиса принято записывать в виде xf = (Ce→f)− 1·xe
47. Понятие линейного подпространства. Подпространства решений однородной системы линейных алгебраических уравнений. Подпространство Алгебраическое определение: Линейное подпространство или векторное подпространство ― непустое подмножество K линейного пространства L такое, что K само является линейным пространством по отношению к определенным в L действиям сложения и умножения на скаляр. Множество всех подпространств обычно обозначают как Lat (L). Чтобы подмножество было подпространством, необходимо и достаточно, чтобы § § для всякого вектора § для всяких векторов Последние два утверждения эквивалентны следующему: § для всяких векторов В частности, пространство, состоящее из одного элемента {θ}, является подпространством любого пространства; любое пространство является само себе подпространством. Подпространства, не совпадающие с этими двумя, называют собственными или нетривиальными. Свойства подпространств: § Пересечение любого семейства подпространств — снова подпространство; § Сумма конечного семейства подпространств — снова подпространство. Сумма подпространств
В функциональном анализе в бесконечномерных пространствах особо выделяют замкнутые подпространства.
48. Линейные операторы (примеры) Примеры линейных однородных операторов: § оператор дифференцирования: § оператор интегрирования: § оператор умножения на определённую функцию § оператор интегрирования с заданным «весом» § оператор взятия значения функции f в конкретной точке x 0: L { f } = f (x 0)[4]; § оператор умножения вектора на матрицу: b = Ax; § оператор поворота вектора. Примеры линейных неоднородных операторов: § Любое аффинное преобразование; § § § где
49. Матрица линейного оператора. Определение координат образа вектора линейного пространства при действии на него линейного оператора. Матрица линейного оператора — матрица, выражающая линейный оператор в некотором базисе. Для того, чтобы ее получить, необходимо подействовать опер
|
||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 2638; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.70.69 (0.012 с.) |

 Дважды транспонированная матрица А равна исходной матрице А.
Дважды транспонированная матрица А равна исходной матрице А. Транспонированная сумма матриц равна сумме транспонированных матриц.
Транспонированная сумма матриц равна сумме транспонированных матриц.  Транспонированное произведение матриц равно произведению транспонированных матриц
Транспонированное произведение матриц равно произведению транспонированных матриц При транспонировании можно выносить скаляр
При транспонировании можно выносить скаляр Определитель транспонированной матрицы равен определителю исходной матрицы.
Определитель транспонированной матрицы равен определителю исходной матрицы. определителя
определителя  – го порядка называют определитель
– го порядка называют определитель  – го порядка, который получается из данного определителя вычеркиванием
– го порядка, который получается из данного определителя вычеркиванием 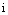 - й строки и
- й строки и  – го столбца, на пересечении которых стоит элемент
– го столбца, на пересечении которых стоит элемент  – четное число и со знаком минус в противном случае.
– четное число и со знаком минус в противном случае. .
. . (Это определение вводится по аналогии с умножением чисел)
. (Это определение вводится по аналогии с умножением чисел)





 линейно независимых решения системы.
линейно независимых решения системы.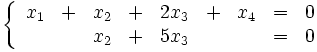
 и
и  в качестве главных переменных. Тогда:
в качестве главных переменных. Тогда:
 и
и  .
.
 ,
, составляют фундаментальную систему решений.
составляют фундаментальную систему решений.
 — её расширенная матрица.
— её расширенная матрица. (т.е. система (2) совместна), тогда:
(т.е. система (2) совместна), тогда: , где
, где  — число переменных системы (2), то решение (2) существует и оно единственно;
— число переменных системы (2), то решение (2) существует и оно единственно; , то общее решение системы (2) имеет вид
, то общее решение системы (2) имеет вид  , где
, где  — общее решение системы (1), называемое общим однородным решением,
— общее решение системы (1), называемое общим однородным решением,  — частное решение системы (2), называемое частным неоднородным решением.
— частное решение системы (2), называемое частным неоднородным решением.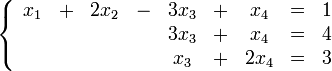

 и
и  обязательно будут главными, возьмём также
обязательно будут главными, возьмём также  является частным решением.
является частным решением.


 . Определитель матрицы
. Определитель матрицы  равен нулю, так как третья строка равна сумме первых двух. Минор второго порядка, расположенный в первых двух строках и первых двух столбцах, равен
равен нулю, так как третья строка равна сумме первых двух. Минор второго порядка, расположенный в первых двух строках и первых двух столбцах, равен 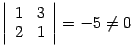 . Следовательно, ранг матрицы равен двум, и рассмотренный минор является базисным.
. Следовательно, ранг матрицы равен двум, и рассмотренный минор является базисным. Могут возникать следующие варианты:
Могут возникать следующие варианты:
 и корни характеристического уравнения
и корни характеристического уравнения  (см. выше раздел «Характеристическая квадратичная форма и характеристическое уравнение»).
(см. выше раздел «Характеристическая квадратичная форма и характеристическое уравнение»).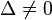 )
)












 находится в начале координат.
находится в начале координат.
 (эксцентриситет) от данной точки (фокуса) и от данной прямой (директрисы) постоянно. Кроме того, при
(эксцентриситет) от данной точки (фокуса) и от данной прямой (директрисы) постоянно. Кроме того, при  кривая является окружностью, при
кривая является окружностью, при  — эллипсом, при
— эллипсом, при  — параболой, при
— параболой, при  — гиперболой.
— гиперболой. а координаты фокуса
а координаты фокуса  Директриса перпендикулярна оси симметрии, проходящей через фокус и вершину кривой (фокальная ось). Расстояние между фокусом и директрисой равно
Директриса перпендикулярна оси симметрии, проходящей через фокус и вершину кривой (фокальная ось). Расстояние между фокусом и директрисой равно 

 фокус невырожденной кривой второго порядка, а в качестве полярной оси — её ось симметрии, то в полярных координатах ρ, φ уравнение кривой будет иметь вид
фокус невырожденной кривой второго порядка, а в качестве полярной оси — её ось симметрии, то в полярных координатах ρ, φ уравнение кривой будет иметь вид
 имеет вид:
имеет вид:



 -вектор нормали к плоскости.
-вектор нормали к плоскости.
 или
или 
 и прямая
и прямая

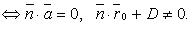
 то случаи 1 - 3 имеют место, когда:
то случаи 1 - 3 имеют место, когда:


 задана точкой
задана точкой  и двумя векторами
и двумя векторами  и
и  Прямая в пространстве задана двумя точками
Прямая в пространстве задана двумя точками  и
и  (рис.1-1). Если точка
(рис.1-1). Если точка  является точкой пересечения плоскости
является точкой пересечения плоскости 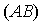 , то ее координаты должны удовлетворять уравнению
, то ее координаты должны удовлетворять уравнению  . С другой стороны, точка
. С другой стороны, точка  . Подставив в уравнение принадлежности точки
. Подставив в уравнение принадлежности точки  . Откуда следует, что:
. Откуда следует, что: 


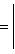









 данной точки от данной прямой есть расстояние от этой точки до прямой, которому приписывается знак плюс, если точка и начало координат находятся по разные стороны от прямой, и знак минус, если точка и начало координат находятся по одну сторону от прямой.
данной точки от данной прямой есть расстояние от этой точки до прямой, которому приписывается знак плюс, если точка и начало координат находятся по разные стороны от прямой, и знак минус, если точка и начало координат находятся по одну сторону от прямой.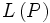 над полем P — это непустое множество L, на котором введены операции
над полем P — это непустое множество L, на котором введены операции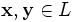 ставится в соответствие элемент того же множества, обозначаемый
ставится в соответствие элемент того же множества, обозначаемый 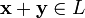 и
и и любому элементу
и любому элементу  ставится в соответствие элемент из
ставится в соответствие элемент из 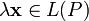 .
.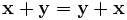 , для любых
, для любых  , для любых
, для любых  (ассоциативность сложения);
(ассоциативность сложения);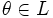 , что
, что 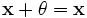 для любого
для любого  , что
, что 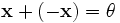 (существование противоположного элемента).
(существование противоположного элемента).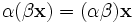 (ассоциативность умножения на скаляр);
(ассоциативность умножения на скаляр);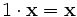 (умножение на нейтральный (по умножению) элемент поля P сохраняет вектор).
(умножение на нейтральный (по умножению) элемент поля P сохраняет вектор).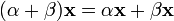 (дистрибутивность умножения на вектор относительно сложения скаляров);
(дистрибутивность умножения на вектор относительно сложения скаляров);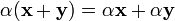 (дистрибутивность умножения на скаляр относительно сложения векторов).
(дистрибутивность умножения на скаляр относительно сложения векторов). для любого
для любого 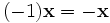 для любого
для любого 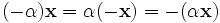 для любых
для любых 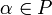 и
и  для любого
для любого 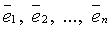 из n линейно независимых векторов пространства
из n линейно независимых векторов пространства 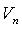 .
.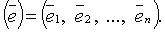
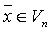 существуют числа
существуют числа 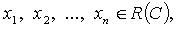 такие что
такие что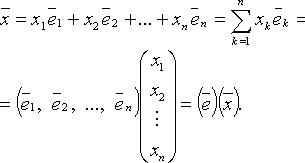
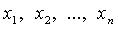 называются координатами вектора
называются координатами вектора 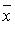 в базисе (
в базисе (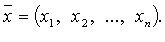
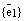 –базис
–базис 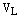 . Возьмем произвольный вектор
. Возьмем произвольный вектор  . Так как оба вектора
. Так как оба вектора  и
и 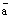 коллинеарные одной и той же прямой L, то
коллинеарные одной и той же прямой L, то 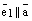 . Воспользуемся теоремой о коллинеарности двух векторов. Так как
. Воспользуемся теоремой о коллинеарности двух векторов. Так как 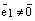 , то найдется (существует) такое число
, то найдется (существует) такое число 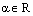 , что
, что 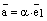 и тем самым мы получили разложение вектора
и тем самым мы получили разложение вектора 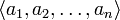 к базису
к базису  является матрица, столбцы которой — координаты разложения векторов
является матрица, столбцы которой — координаты разложения векторов 
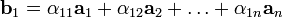 .
.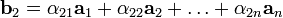 .
.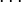 .
. .
.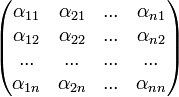

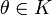 ;
;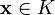 , вектор
, вектор 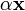 также принадлежал K, при любом
также принадлежал K, при любом 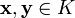 , вектор
, вектор 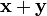 также принадлежал K.
также принадлежал K.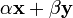 также принадлежал K для любых
также принадлежал K для любых 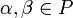 .
.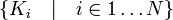 определяется как множество, содержащее всевозможные суммы элементов Ki:
определяется как множество, содержащее всевозможные суммы элементов Ki: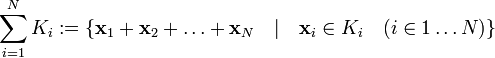 .
.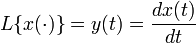 ;
;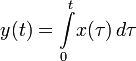 ;
;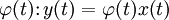 ;
;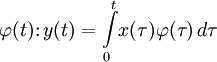
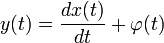 ;
;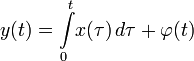 ;
;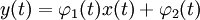 ;
;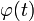 ,
,  ,
, 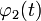 — вполне определённые функции, а x (t) — преобразуемая оператором функция.
— вполне определённые функции, а x (t) — преобразуемая оператором функция.


