
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейные операции над матрицами.Содержание книги Поиск на нашем сайте
Матрицы
Основные понятия.
Опр. Числовая матрица размерности m´n – это прямоугольная таблица чисел, состоящая из m строк и n столбцов. Строки матрицы – это горизонтальные ряды чисел, столбцы матрицы – это вертикальные ряды чисел. Числа матрицы называются элементами матрицы. Матрицы обычно заключены в круглые скобки. Обозначаются матрицы заглавными буквами латинского алфавита, а их элементы - соответствующими малыми буквами с двумя индексами. Например, для матрицы А, ее элементы обозначаются символами аij, где первый индекс i указывает номер строки, а второй индекс j – номер столбца данного элемента (i =
i
Рисунок 1.1
Матрица А размерности m´n кратко обозначается символом Am´n и имеет вид
Am´n =
Виды матриц.
Если в матрице Am´n число строк не равно числу столбцов (m
An =
NB. Квадратная матрица 1-го порядка А1 состоит из одного элемента а11. Матрица, состоящая из одной строки (m=1), называется матрицей-строкой или строчной матрицей. Например, A1´n = (a11 a12 … a1n) Матрица, состоящая из одного столбца (n = 1), называется матрицей–столбцом или столбцевой матрицей. Например, Am´1 =
Нулевая матрица – это матрица, у которой все элементы равны нулю. Нулевая матрица обозначается буквой О: О = NB. В матричном исчислении нулевая матрица играет ту же роль, что и число 0 в арифметике. Квадратные матрицы.
Элементы с одинаковыми индексами a11, а22, …, ann образуют главную диагональ квадратной матрицы. Поэтому эти элементы называются диагональными элементами. Геометрически главная диагональ проходит через левый верхний и правый нижний угол квадратной матрицы (рис.1.2).
Рисунок 1.2
Соответственно побочная диагональ квадратной матрицы проходит через ее правый верхний и левый нижний угол (рис.1.3).
Рисунок 1.3
Диагональная матрица – это квадратная матрица, у которой все элементы, лежащие вне главной диагонали равны нулю. A = NB. В диагональной матрице среди ее диагональных элементов могут быть и нули, но только не на концах главной диагонали, т.е. а11¹0, аnn¹0.
Частным случаем диагональной матрицы является единичная матрица. Единичная матрица - это диагональная матрица, у которой все диагональные элементы равны единице. Она обозначается буквой Е. E = Ее краткое обозначение E = NB. В матричном исчислении единичная матрица играет ту же роль, что и число 1 в арифметике. Треугольная матрица – это квадратная матрица, у которой все элементы, расположенные выше (или ниже) главной диагонали, равны нулю. В верхней треугольной матрице равны нулю все элементы, расположенные ниже главной диагонали. В нижней треугольной матрице равны нулю все элементы, расположенные выше главной диагонали.
Действия над матрицами
Транспонирование матриц. Опр. Если в матрице А поменять местами строки на столбцы с сохранением их нумерации, то получится транспонированная матрица Ат. Пример. Дано: А= А2×4 Решение: 1) Ат =
Свойства операции транспонирования: 1) (Ат)т=А; 2) (А+В)т=Ат+Вт; 3) (l×А)т=l×Ат; 4) (А×В)т=Вт×Ат. NB. Транспонирование квадратной матрицы сводится к повороту ее элементов вокруг главной диагонали на угол p. Опр. Симметрические матрицы – это квадратные матрицы, у которых равны элементы, симметричные относительно главной диагонали, то есть aij = aji.
Определители
Понятие определителя.
Определитель – это число, которое является характеристикой данной квадратной матрицы. Определители существуют только для квадратных матриц. Чтобы подчеркнуть связь между квадратной матрицей и ее определителем, его обозначают также как и матрицу, к которой он относится, только меняют форму скобок. Если в матрице элементы ограничены двумя круглыми скобками, то, выпрямив скобки до прямых вертикальных линий, мы получим определитель. При этом элементы матрицы автоматически становятся элементами определителя, который кратко обозначается одним из символов D, |An|, detA. An = NB. Хотя внешне квадратная матрица и ее определитель отличаются только формой скобок, но между ними есть принципиальное отличие. Матрица – это таблица чисел, а ее определитель – это одно число, которое характеризует эту квадратную матрицу.
Свойства определителей.
1) При транспонировании определителя его значение не меняется, (то есть значение определителя не меняется при замене его строк столбцами с теми же номерами). Доказательство: D = NB. Следовательно, строки и столбцы определителя равноправны, поэтому его свойства можно формулировать и доказывать либо для строк, либо для столбцов. 2) При взаимной перестановке любых двух строк (столбцов) определителя его знак меняется на противоположный. Доказательство: D =
3) Определитель с двумя одинаковыми строками (столбцами) равен нулю. Доказательство. Пусть определитель D имеет две одинаковые строки. Если поменять их местами, то, с одной стороны, величина определителя не изменится, так как строки одинаковы, а с другой стороны определитель должен поменять свой знак на противоположный по свойству 2. Таким образом, имеем: D = -D Þ D = 0. 4) Общий множитель элементов какой-либо строки (столбца) можно выносить за знак определителя. Доказательство: D= Следствие: D = NB. Правило умножения определителя на число. Чтобы умножить определитель на число, надо все элементы какой-то одной его строки (столбца) умножить на это число. 5) Определитель с нулевой строкой (столбцом) равен нулю. Доказательство. По свойству 4 вынесем общий множитель l = 0 элементов нулевой строки (столбца) за знак определителя. Получим 0×D = 0. 6) Определитель с двумя и более пропорциональными строками (столбцами) равен нулю. Доказательство. Если вынести за знак определителя коэффициент пропорциональности двух строк (столбцов) l≠0, то получится определитель с двумя одинаковыми строками (столбцами), равный нулю по свойству 3. 7) Если каждый элемент какой-либо строки (столбца) определителя представить в виде суммы k слагаемых, то такой определитель равен сумме k определителей, у которых элементы этой строки (столбца) заменены соответствующими слагаемыми, а все остальные элементы такие же как у исходного определителя. Доказательство: D=
Опр. n-ая строка определителя называется линейной комбинацией его остальных (n-1) строк, если ее можно представить в виде суммы произведений этих строк на соответствующие числа l1, l2, …, ln-1. Например, в определителе
3–я строка является линейной комбинацией первых двух строк. NB. Линейная комбинация называется тривиальной, если в ней "li = 0. В противном случае линейная комбинация называется нетривиальной (if $li ¹ 0). 8 а) Если одна строка (столбец) определителя является линейной комбинацией других его строк (столбцов), то такой определитель равен нулю. Доказательство: D =
Доказательство: Пусть D= Þ 9) Сумма произведений элементов какой-либо строки (столбца) определителя на алгебраические дополнения соответствующих элементов любой другой строки (столбца) определителя равна нулю, то есть
D = Тогда а11А21 + а12А22 + а13А23 = 0, так как выполнено умножение элементов 1-ой строки определителя на алгебраические дополнения соответствующих элементов 2-ой строки. Доказательство: а11А21 + а12А22 + а13А23 = а11×(-1)2+1 ={это есть разложение по 1-й строке определителя (-1)× Если определитель D¹0, то по свойству 8 б) в нем всегда можно «обнулить» i-ю строку (j-й столбец) до единственного ненулевого элемента и разложить определитель по этой строке (столбцу). Применяя эту операцию нужное число раз, всегда можно из определителя n-го порядка получить определитель 2-го порядка. Пример 1. Вычислить определитель D = Решение: Используя свойство 8 б) определителей, проще всего 2-ую строку «обнулить» до единственного ненулевого элемента, так как ее элементы минимальны по абсолютной величине и она уже содержит один ноль. Для этой цели выберем в определителе так называемый активный столбец, ненулевой элемент которого стоящий на пересечении с обнуляемой строкой должен быть минимальным по модулю из всех элементов этой строки (оптимально, если он равен ±1.). В данном случае таких столбцов два: 1-ый и 3-ий. Возьмем в качестве активного 3-ий столбец, так как у него со 2-ой строкой общий элемент а23=1 и по сравнению с 1-ым столбцом его элементы по модулю меньше. Чтобы обнулить 1-ый элемент 2-ой строки, умножим активный столбец на (-1) и прибавим его к 1-му столбцу. Аналогично, чтобы обнулить 4-ый элемент 2-ой строки, умножим активный столбец на (-2) и прибавим его к 4-му столбцу. В результате, во 2-ой строке останется только один ненулевой элемент а23=1 (который принадлежит активному столбцу). Запишем эти действия:
Пример 2. Вычислить определитель D =
NB 1. В случае если обнуляющий элемент активной строки (столбца) не равен ±1, то, используя линейную комбинацию соответствующих строк (столбцов), всегда можно добиться того, чтобы он стал равен ±1.
Пример 3. Вычислить определитель
NB 2. Определитель треугольного вида равен произведению его диагональных элементов, то есть
Доказательство. Последовательно разлагая определитель треугольного вида D= D = а11×а22 ×××аnn = Пример 4. Вычислить определитель сведением его к треугольному виду. D= Решение. Чтобы свести определитель к треугольному виду, необходимо в 1-ом столбце обнулить три элемента, во 2-ом – два, в 3-ем – один и опустить их вниз, чтобы все они были под главной диагональю. Начнем обнуление с 1-го столбца. Для этой цели выберем в качестве активной 2-ую строку, у которой 1-ый элемент равен 1, а остальные элементы минимальны по модулю по сравнению с элементами 1-ой и 4-ой строк. С помощью этой активной строки обнулим 1-ый столбец.
Невырожденные матрицы.
Обратная матрица. Опр. Матрица
Опр. Квадратная матрица А называется вырожденной (особенной), если ее определитель |A|=0, и невырожденной, если ее определитель |A|¹0. Опр. Квадратная матрица А-1 называется обратной (инверсной) к квадратной матрице А, если выполняется условие А-1×А = А×А-1= Е (3.2) NB. Обратная матрица А-1 возможна только для невырожденной матрицы А. Теорема. Для любой невырожденной квадратной матрицы А существует единственная обратная матрица А-1, которая находится по формуле А-1 = Доказательство. 1) Из определения А-1×А = А×А-1 следует, что А и А-1- это квадратные матрицы одного порядка.
Пусть матрица А – невырожденная, то есть |A|¹0. Тогда, по правилу умножения матриц, по теореме Лапласа и по свойству 9 определителей, получим А× = |A|× Следовательно, А× Из А× 2) Докажем единственность обратной матрицы. Предположим, что для матрицы А существует еще одна обратная матрица В. Тогда, согласно определению произведение А×В=Е. Обе части последнего равенства умножим слева на обратную матрицу А-1 и получим: А-1×А×В = А-1×Е Þ Е×В = А-1×Е Þ В = А-1. Fin.
Свойства обратной матрицы: 1) |A-1| = 2) (A×B)-1 = B-1×A-1; 3) (A-1)т = (Ат)-1.
3.1.1. Вычисление обратной матрицы А-1 с помощью присоединенной матрицы
Для этого необходимо: 1) Вычислить определитель |A|. Если |A|=0, следовательно матрица А – вырожденная и для нее нет обратной матрицы А-1. Если же |A|¹0, то следует выполнить следующие действия. 2) Вычислить алгебраические дополнения Aij всех элементов aij матрицы А и построить матрицу АА, в которой на местах элементов aij будут стоять их алгебраические дополнения Aij: АА = 3) Транспонировать матрицу АА, чтобы получить присоединенную матрицу
4) Вычислить обратную матрицу А-1 по формуле: А-1 = 5) Выполнить проверку: А-1×А = Е.
Пример. Дано: А= Решение: 1) Вычислим определитель |A|. Для этого сначала «обнулим» первый столбец, а затем приведем определитель к треугольному виду.
А11=(-1)2 А21=(-1)3 А31=(-1)4 3) Составим матрицу АА из алгебраических дополнений Aij и транспонируем ее, чтобы получить присоединенную матрицу АА= 4) Найдем обратную матрицу по формуле: А-1 = NB. В случае, когда |A| ¹ ±1, множитель 5) Проверка: А-1×А = Ответ: А-1 = 3.1.2. Вычисление обратной матрицы А-1 методом элементарных преобразований над строками матрицы.
Элементарными преобразованиями матрицы называются: 1) перестановка строк (столбцов) матрицы; 2) умножение элементов строки (столбца) на число l¹0; 3) прибавление элементов одной строки (столбца) к соответствующим элементам другой строки (столбца); 4) вычеркивание нулевой строки (столбца) матрицы. NB. При элементарных преобразованиях получают только эквивалентные матрицы. Опр. Матрицы А и В называются эквивалентными (A~B), если одна из них получается из другой в результате конечного числа элементарных преобразований. Суть метода элементарных преобразований над строками матрицы. К исходной квадратной матрице An справа через разделительную вертикальную черту приписывают единичную матрицу Е того же порядка, что и А, и таким образом получают расширенную матрицу (A|E). Далее, с помощью элементарных преобразований над строками приводят матрицу (A|E) сначала к ступенчатому виду (А1|B), где А1 – верхняя треугольная матрица, а затем к виду (Е|А-1). Таким образом, имеет место преобразование: (А|Е)Þ(Е|А-1).
Пример. Дано: А=
Проверка: А-1×А =
Ранг матрицы
Если в прямоугольной матрице Аm´n выделить любые k строк и k столбцов (k Опр. Минор k–го порядка Мk матрицы А называется базисным минором, если сам он не равен нулю, а все миноры более высоких порядков равны нулю. NB. В матрице может быть несколько базисных миноров, но все они будут одного порядка. NB. Строки и столбцы базисного минора называются базисными строками и столбцами. Опр. Ранг матрицы есть порядок ее базисного минора. Ранг матрицы А обозначается символом r(A) или rang A. NB.Только для нулевой матрицы О ее ранг r(O)=0.
Ранг матрицы не меняется:
1) при транспонировании матрицы; 2) если в матрице приписать или вычеркнуть нулевую строку (столбец); 3) при элементарных преобразованиях матрицы.
Опр. Матрица называется ступенчатой, если в каждой ее строке, начиная со второй, первый ненулевой элемент от начала строки расположен строго правее, чем первый ненулевой элемент предыдущей строки. Например,
NB. С помощью элементарных преобразований матрицу всегда можно привести к ступенчатому виду Опр. Ранг ступенчатой матрицы равен числу ее ненулевых строк. NB. В ступенчатой матрице всегда можно выделить базисный минор треугольного вида с ненулевыми диагональными элементами, порядок которого равен числу ненулевых строк. Например, в матрице А можно выделить два таких базисных минора
Пример. Найти ранг матрицы А= Решение. Элементарными преобразованиями приведем матрицу А к ступенчатому виду.
Ответ: r(A) = 3
Основные понятия.
Опр. Система линейных алгебраических уравнений (СЛАУ), состоящая из m уравнений с n неизвестными x1, …, xn имеет следующий вид
где числа aij (i = NB. Система алгебраических уравнений называется линейной, если все уравнения системы содержат неизвестные только в первой степени, причем они между собой не перемножаются. СЛАУ называется квадратной, если в ней число уравнений равно числу неизвестных, то есть m = n. СЛАУ называется однородной, если все ее свободные члены равны нулю, то есть "bi=0 (i = СЛАУ называется неоднородной, если среди ее свободных членов хотя бы один не равен нулю, то есть $bi¹0. Решением СЛАУ называется такая совокупность значений неизвестных x1= C1, x2= C2,…, xn = Cn, которая каждое уравнение СЛАУ обращает в верное числовое равенство (тождество). СЛАУ называется совместной, если она имеет хотя бы одно решение, и, соответственно, несовместной, есл
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 383; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.254.160 (0.015 с.) |

 ; j =
; j =  ) (рис.1.1).
) (рис.1.1).

 j
j

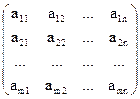
 n), то такая матрица называется прямоугольной, а если m = n, то такая матрица называется квадратной матрицей n-го порядка и она обозначается символом An:
n), то такая матрица называется прямоугольной, а если m = n, то такая матрица называется квадратной матрицей n-го порядка и она обозначается символом An: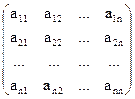







 , где dij – это символ Кронекера,
, где dij – это символ Кронекера, 

 . Найти: 1) Ат, 2) А∙ Ат
. Найти: 1) Ат, 2) А∙ Ат С2×2
С2×2 ; 2) А∙ Ат =
; 2) А∙ Ат =  ∙
∙  =
= 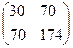
 = D, |An|, detA.
= D, |An|, detA. =
=  = a11×a22 - а12×а21
= a11×a22 - а12×а21
 = la11×a22 - lа12×а21 = l(a11×a22 - а12×а21) = l
= la11×a22 - lа12×а21 = l(a11×a22 - а12×а21) = l 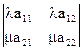 = l×m
= l×m  .
. = (а11 + b11)а22 - (а12 + b12)а21 = (а11а22 - а12а21) + (b11а22 - b12а21) = =
= (а11 + b11)а22 - (а12 + b12)а21 = (а11а22 - а12а21) + (b11а22 - b12а21) = =  .
.

 =
=  = 0 (if i ≠ j).Например, пусть
= 0 (if i ≠ j).Например, пусть ¹ 0
¹ 0 + а12×(-1)2+2
+ а12×(-1)2+2 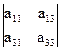 + а13×(-1)2+3
+ а13×(-1)2+3 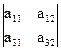 =
=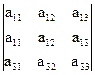 = 0}= 0.
= 0}= 0.


 -1 -2
-1 -2 D=
D=  = {разложим определитель по 2-ой строке согласно правилу разложения определителя по элементам строки (столбца)} = а23×А23 = =1×(-1)2+3×М23 = -
= {разложим определитель по 2-ой строке согласно правилу разложения определителя по элементам строки (столбца)} = а23×А23 = =1×(-1)2+3×М23 = -  = {вынесем за знак определителя множитель (-2) 1-й строки и для «обнуления» этой строки используем 2-ой столбец в качестве активного}=
= {вынесем за знак определителя множитель (-2) 1-й строки и для «обнуления» этой строки используем 2-ой столбец в качестве активного}=

 1 1
1 1 = 2×
= 2×  = 2×
= 2×  = {разложим определитель по 1-ой строке}= =2×(-1)×(-1)1+2×
= {разложим определитель по 1-ой строке}= =2×(-1)×(-1)1+2×  ={вынесем за знак определителя множитель (3) 1-го столбца}= =2×3×
={вынесем за знак определителя множитель (3) 1-го столбца}= =2×3×  = 6×(-3-1) = -24.
= 6×(-3-1) = -24.






 Решение. D=
Решение. D=  = 2
= 2  = 2×а24×А24 =2×1×(-1)6×М24 =2
= 2×а24×А24 =2×1×(-1)6×М24 =2  = =2×4×(-1)3×
= =2×4×(-1)3×  = 8×
= 8×  = 8×(11-20) = -72
= 8×(11-20) = -72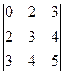



 Решение.
Решение.  =
=  -2 =
-2 =  = 1×(-1)3+1
= 1×(-1)3+1  = 4-3 = 1
= 4-3 = 1 =
=  = а11×а22×××аnn
= а11×а22×××аnn .
.
















 D=
D=  =
=  = {Вынесем общий множитель 1-ой и 2-ой строк за знак определителя и переставим местами эти строки, чтобы опустить вниз все нули в1-м столбце}= 2×
= {Вынесем общий множитель 1-ой и 2-ой строк за знак определителя и переставим местами эти строки, чтобы опустить вниз все нули в1-м столбце}= 2×  = {Получилась так называемая 1-ая ступенька, которая отделяет 1-ую строку от остальных трех симметричных строк одинаково начинающихся с нулевых элементов. Это означает, что 1-ая строка больше не участвует в дальнейших преобразованиях, а мы продолжаем работать с тремя оставшимися симметричными строками. Из этих строк выбираем в качестве активной 2-ую строку, так как ее элементы минимальны по модулю, и с ее помощью обнуляем два элемента во 2-ом столбце, согласно схемы}= 2×
= {Получилась так называемая 1-ая ступенька, которая отделяет 1-ую строку от остальных трех симметричных строк одинаково начинающихся с нулевых элементов. Это означает, что 1-ая строка больше не участвует в дальнейших преобразованиях, а мы продолжаем работать с тремя оставшимися симметричными строками. Из этих строк выбираем в качестве активной 2-ую строку, так как ее элементы минимальны по модулю, и с ее помощью обнуляем два элемента во 2-ом столбце, согласно схемы}= 2×  = {Получился определитель с двумя ступеньками, которые означают, что 1-ая и 2-ая строки завершены и больше не участвуют в дальнейших преобразованиях. Мы продолжаем работать с двумя оставшимися симметричными строками, из которых выбираем в качестве активной 3-ю строку и обнуляем последний элемент в 3-ем столбце. В результате получился определитель треугольного вида, у которого все элементы ниже главной диагонали равны нулю}=
= {Получился определитель с двумя ступеньками, которые означают, что 1-ая и 2-ая строки завершены и больше не участвуют в дальнейших преобразованиях. Мы продолжаем работать с двумя оставшимися симметричными строками, из которых выбираем в качестве активной 3-ю строку и обнуляем последний элемент в 3-ем столбце. В результате получился определитель треугольного вида, у которого все элементы ниже главной диагонали равны нулю}=

 = 2∙(1∙1∙3∙(-4)) = 2×(-12) = -24
= 2∙(1∙1∙3∙(-4)) = 2×(-12) = -24

 называется присоединенной (союзной) к квадратной матрице А, если она состоит из алгебраических дополнений элементов транспонированной матрицы Ат. Чтобы получить присоединенную матрицу
называется присоединенной (союзной) к квадратной матрице А, если она состоит из алгебраических дополнений элементов транспонированной матрицы Ат. Чтобы получить присоединенную матрицу  (3.1)
(3.1) (3.3)
(3.3) =
= = |A|×E
= |A|×E = А-1×|A|×E Þ Е×
= А-1×|A|×E Þ Е×  ;
; .
.
 :
: =
=  =
=  , А-1=?
, А-1=?



 |A| =
|A| =  =
=  = –
= –  = -(–7) = 7 ¹ 0 Þ $ А-1.
= -(–7) = 7 ¹ 0 Þ $ А-1. 2) Найдем алгебраические дополнения Aij всех элементов aij матрицы А:
2) Найдем алгебраические дополнения Aij всех элементов aij матрицы А: = -2; А12=(-1)3
= -2; А12=(-1)3  = 1; А13=(-1)4
= 1; А13=(-1)4  = 0;
= 0; = -3; А22=(-1)4
= -3; А22=(-1)4  = –16; А23=(-1)5
= –16; А23=(-1)5  = 14;
= 14; = 3; А32=(-1)5
= 3; А32=(-1)5  = 9; А33=(-1)6
= 9; А33=(-1)6 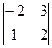 = –7.
= –7. Þ
Þ  =
=  .
. ∙
∙ 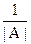 лучше оставлять вне обратной матрицы А-1 для удобства проверки.
лучше оставлять вне обратной матрицы А-1 для удобства проверки. =
=  =
=  = Е.
= Е. . Методом элементарных преобразований над строками найти обратную матрицу А-1.
. Методом элементарных преобразований над строками найти обратную матрицу А-1.



 Решение. (A|E) =
Решение. (A|E) =  -1 ~
-1 ~  ~ ~
~ ~  ~
~  ~
~  -1 ~
-1 ~
 ~
~  ~
~  Þ ÞА-1=
Þ ÞА-1= 
 ×
×  = Е
= Е min(m,n)), то элементы, стоящие на пересечении этих строк и столбцов, образуют квадратную матрицу k–го порядка Аk. Определитель квадратной матрицы Аk называется минором k–го порядка исходной прямоугольной матрицы Аm´n, который обозначается символом Мk.
min(m,n)), то элементы, стоящие на пересечении этих строк и столбцов, образуют квадратную матрицу k–го порядка Аk. Определитель квадратной матрицы Аk называется минором k–го порядка исходной прямоугольной матрицы Аm´n, который обозначается символом Мk.


 или В =
или В = 


 и М’4=
и М’4=  , а в матрице В только один: М4=
, а в матрице В только один: М4= 








 А=
А=  ~
~  ~
~  ~
~

 = В Þ r(B) = 3. Так как А~В Þ r(А) = r(B) = 3.
= В Þ r(B) = 3. Так как А~В Þ r(А) = r(B) = 3. , (4.1)
, (4.1)


