
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Образец выполнения индивидуальной домашней работы (ИДР).Содержание книги
Поиск на нашем сайте
1) Пользуясь свойствами определителей, доказать тождество Решение. Пользуясь свойствами определителей 7), 4) и 6), получим
2) Дано: А = Решение.
3) Решить квадратную СЛАУ а) матричным способом; б) по формулам Крамера. 3а) Решение квадратной СЛАУ матричным способом В этой СЛАУ А= α) Методом элементарных преобразований найдем обратную матрицу А-1:
β) Проверка: А-1×А = γ) По формуле (4.3) находим решение СЛАУ: Х=А-1×В Þ δ) Проверка. Подставляя значения х1 = 1, х2 = 2, х3 = -1 в исходную систему уравнений, получим 2×1+3×2+5×(-1)=3 Û 3º3 1+2+(-1)=2 Û 2º2 1+3×2-2×(-1)=9 Þ 9º9 Ответ: х1 = 1, х2 = 2, х3 = -1. 3б) Решение квадратной СЛАУ по формулам Крамера: Главный определитель системы равен
Þ х1 =
Ответ: х1 = 1, х2 = 2, х3 = -1. 4) Выполнить действия над матрицами: (А-1)2 + В×А, если А= а) Методом элементарных преобразований над строками найдем обратную матрицу А-1.
Проверка: А-1×А = б) (А-1)2 = в) В×А = 5) Найти значения l, для которых существует обратная матрица А-1, если А= Решение. Обратная матрица А-1 существует, когда исходная матрица А является невырожденной, то есть ее определитель |А| ¹ 0. Найдем значения l, при которых определитель |А| = 0 и, исключив их, определим те значения l, при которых обратная матрица А-1 существует. Для этого разложим определитель данной матрицы по 3–му столбцу, так как он содержит только один ненулевой элемент (λ–2):
а) l = 2; б) (l-2)2 - –1 = 0 Þ l2 - 4l + 3 = 0 Þ Таким образом, при l = 1; 2; 3 обратная матрица А-1 не существует. Значит, она существует во всех остальных случаях, когда l ¹ 1; 2; 3. Ответ: Обратная матрица А-1 существует при l ¹ 1; 2; 3. 6) Найти ранг r(А) матрицы А, если А=
Решение. Элементарными преобразованиями приведем матрицу А к ступенчатому виду.
7(а) Исследовать СЛАУ на совместность и решить методом Гаусса.
Решение. Запишем расширенную матрицу СЛАУ и элементарными преобразованиями над строками приведем ее к ступенчатому виду.
Проверка: 2×(-2)-2×1+3+3=0 Û 0º0 2×(-2)+3×1+4-3×3+6=0 Û 0º0 3×(-2)+4×1-4+2×3=0 Û 0º0 -2+3×1+4-3-2=0 Û 0º0 Ответ: х1 = -2, х2 = 1, х3 = 4, х4 = 3. 7(б) Исследовать СЛАУ на совместность и решить методом Гаусса.
Решение. Запишем расширенную матрицу СЛАУ и элементарными преобразованиями над строками приведем ее к ступенчатому виду.
Поскольку число уравнений больше числа неизвестных, то нужно выбрать базисные неизвестные. В качестве базисных можно взять неизвестные х1, х2, так как коэффициенты при них образуют один из базисных миноров М2 = Следовательно, остальные неизвестные х3, х4 – свободные. Зафиксируем их и, чтобы отличить от базисных неизвестных, переобозначим: пусть х3 = с3, х4 = с4. Перенесем их в правую часть соответствующих уравнений и выразим через них базисные неизвестные х1 и х2:
Ответ: х1 = 1/11(1-14с3+2с4); х2 = 1/11(2-6с3-7с4); х3 = с3; х4 = с4 8) Найти ненулевые решения однородной СЛАУ.
Решение. Запишем расширенную матрицу системы и элементарными преобразованиями над строками приведем ее к ступенчатому виду.
Число неизвестных n = 4 > 2 = r(A) = r(A|B), тогда, по теореме 1 (п.4.6), однородная СЛАУ помимо нулевого решения имеет и ненулевые решения. Найдем их. Полученной ступенчатой матрице В соответствует ступенчатая СЛАУ Чтобы решить ее, в качестве базисных неизвестных можно взять неизвестные х1 и х2, так как коэффициенты при них образуют один из базисных миноров М2 =
Ответ: х1 = 2с3-с4; х2 = 3с3+2с4; х3 = с3; х4 = с4, где с3, с4 - const.
Требования к оформлению студентами индивидуальных домашних работ (ИДР)
1. Вариант ИДР должен соответствовать порядковому номеру фамилии студента в журнале его группы. 2. Каждая ИДР выполняется в отдельной тетради чернилами любого цвета, кроме красного. В тетради должны быть поля для замечаний проверяющего, а в конце тетради должно быть несколько чистых листов для работы над ошибками в соответствии с замечаниями проверяющего. 3. Оформление обложки тетради должно соответствовать образцу: Индивидуальная домашняя работа по высшей математике на тему: Линейная алгебра студента (ки) гр. ……… Ф.И.О. ………………… вариант № ……………. 4. Работа, выполненная по чужому варианту, не засчитывается. 5. Задачи и их решения располагаются в порядке возрастания их номеров в соответствии с нумерацией ИДР. 6. Условие задачи полностью переписывается с заменой общих данных на конкретные из своего варианта. 7. Решение задачи записывается аккуратно и подробно с необходимыми выкладками, чтобы было понятно, откуда что получено. 8. Незачтенная ИДР возвращается студенту для исправления ошибок. Студент должен в конце ИДР в работе над ошибками исправить их и вновь сдать ИДР на проверку.
Список рекомендуемой литературы
1. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры.-М.: Наука, 1984. -320с. 2. Ляпин Е.С., Евсеев А.Е. Алгебра и теория чисел. Ч.2. Линейная алгебра и полиномы.-М.: Просвещение, 1978. - 448с. 3. Гурский Е.И. Основы линейной алгебры и аналитической геометрии.-Минск: Вышейш. шк., 1982. - 272с. 4. Гусак А.А. Высшая математика. Т.1.- Минск: ТетраСистемс, 2001. - 544с. 5. Письменный Д.Т. Конспект лекций по высшей математике. 1 часть.-М.: Рольф, 2000. - 288с. 6. Добротин Д.А. Основы линейной алгебры и аналитической геометрии.-Л.: Изд-во Ленингр. ун-та, 1977. - 120 с. 7. Лунгу К.Н. и др. Сборник задач по высшей математике. 1 курс.-М.: Айрис-пресс, 2003. -576с.
Оглавление Стр.
1. Матрицы…………………………………………………….………………………………….1 1.1. Основные понятия……………………………………….…………………………………..1 1.2. Виды матриц…………………………………………………………………………………1 1.3. Квадратные матрицы………………………………………………………………………..2 1.4. Действия над матрицами……………………………………………………………………3 1.4.1. Линейные действия над матрицами……………………………………………………...3 1.4.2. Умножение матриц………………………………………………………………………..4 1.4.3. Многочлены от квадратных матриц……………………………………………………...6 1.4.4. Транспонирование матриц………………………………………………………………..6 2. Определители………………………………………………………………………………….7 2.1. Понятие определителя………………………………………………………………………7 2.2. Свойства определителей……………………………………………………………………9 3. Невырожденные матрицы…………………………………………………………………...13 3.1. Обратная матрица………………………………………………………………………….13 3.1.1. Вычисление обратной матрицы А-1 с помощью присоединенной матрицы 3.1.2. Вычисление обратной матрицы А-1 методом элементарных преобразований над строками матрицы…….………………………………………………………………………...15
3.2. Ранг матрицы……………………………………………………………………………….16 3.3. Понятие линейной зависимости и линейной независимости..………………………….18 4. Системы линейных алгебраических уравнений (СЛАУ)………………………………….19 4.1. Основные понятия………………………………………………………………………….19 4.2. Матричный способ решения квадратной СЛАУ…………………………………………21 4.3. Формулы Крамера для решения квадратной СЛАУ...…………………………………...22 4.4. Исследование СЛАУ. Теорема Кронекера-Капелли…………………………………….25 4.5. Метод Гаусса исключения неизвестных………………………………………………….26 4.6. Однородная СЛАУ…………………………………………………………………………28 Приложение 1. Индивидуальные задания по теме: «Линейная алгебра»………………..….31 Приложение 2. Образец выполнения индивидуальной домашней работы (ИДР)………….62 Требования к оформлению студентами индивидуальной домашней работы (ИДР)……….68 Список рекомендуемой литературы …………………………………………………………..69
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 251; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.83.45 (0.012 с.) |

 = 0
= 0 +
+  = x×
= x×  +2x×
+2x×  = 0 + 0 = 0.
= 0 + 0 = 0. . Найти АТ; А×АТ и ½А½.
. Найти АТ; А×АТ и ½А½.














 1) АТ =
1) АТ =  ; 2) А×АТ =
; 2) А×АТ =  ; 3)
; 3)  =
=  = =2×
= =2×  = 2×
= 2×  = 2×
= 2×  = 2×(-12) = -24.
= 2×(-12) = -24.
 .
. .
.


 (A|E) =
(A|E) =  ~
~  ~
~  ~
~



 ~
~  -3 ~
-3 ~  ~
~  Þ А-1=
Þ А-1= 
 ×
×  =
=  = Е
= Е =
=  Þ х1 = 1; х2 = 2; х3 = -1
Þ х1 = 1; х2 = 2; х3 = -1


 D=
D=  =
=  =
=  =
=  = 9 ¹ 0 Þ данная СЛАУ имеет единственное решение, определяемое формулами Крамера.
= 9 ¹ 0 Þ данная СЛАУ имеет единственное решение, определяемое формулами Крамера.




 D1 =
D1 =  = -
= -  = -
= -  = -
= -  =
=  = 9 Þ
= 9 Þ = 1.
= 1.





 D2 =
D2 =  =
= 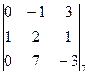 =
=  = -
= -  = 18 Þ х2 =
= 18 Þ х2 =  = 2.
= 2.


 =
=  =
=  = -
= -  = -9 Þ х3 =
= -9 Þ х3 =  = -1.
= -1. , В=
, В=  .
.




 -1 ~
-1 ~  ~
~  ~
~  ~
~  -1 ~
-1 ~

 ~
~  ~
~  Þ ÞА-1=
Þ ÞА-1=  .
. ×
×  = Е;
= Е; ;
; ; г) (А-1)2 + В×А =
; г) (А-1)2 + В×А =  =
=  .
. .
.

 = (-1)6×(l-2)
= (-1)6×(l-2)  = (l-2)×((l-2)2 -1) = 0
= (l-2)×((l-2)2 -1) = 0 = 1; 3.
= 1; 3. .
.



 А=
А=  ~
~  ~
~  ~
~

 = В Þ r(A) = r(B) = 3. Ответ: r(A) = 3
= В Þ r(A) = r(B) = 3. Ответ: r(A) = 3







 ~
~  ~
~  ~
~



























 ~
~  ~
~ 
 ~
~  ~
~ 

 ~
~  ~
~  ~
~  Þ Число неизвестных n = 4 = r(A) = =r(A|B), то есть ранги матрицы коэффициентов и расширенной матриц равны числу неизвестных. Тогда по теореме Кронекера-Капелли данная СЛАУ совместная и определенная. Полученная ступенчатая расширенная матрица СЛАУ соответствует ступенчатой СЛАУ
Þ Число неизвестных n = 4 = r(A) = =r(A|B), то есть ранги матрицы коэффициентов и расширенной матриц равны числу неизвестных. Тогда по теореме Кронекера-Капелли данная СЛАУ совместная и определенная. Полученная ступенчатая расширенная матрица СЛАУ соответствует ступенчатой СЛАУ 




 -2 ~
-2 ~  ~
~  ~ ~
~ ~  Þ Число неизвестных n = 4 > 2 = r(A) = r(A|B). По теореме Кронекера-Капелли данная система совместная и неопределенная. Полученная ступенчатая расширенная матрица СЛАУ соответствует ступенчатой СЛАУ
Þ Число неизвестных n = 4 > 2 = r(A) = r(A|B). По теореме Кронекера-Капелли данная система совместная и неопределенная. Полученная ступенчатая расширенная матрица СЛАУ соответствует ступенчатой СЛАУ 
 = 11 ¹ 0.
= 11 ¹ 0.







 -3 ~
-3 ~  ~
~  = B
= B
 =1¹0. Следовательно, остальные неизвестные – свободные. Переобозначим их: х3 = с3, х4 = с4, и перенесем в правую часть соответствующих уравнений.
=1¹0. Следовательно, остальные неизвестные – свободные. Переобозначим их: х3 = с3, х4 = с4, и перенесем в правую часть соответствующих уравнений.
 …......14
…......14


