
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства линейно зависимых и линейно независимых столбцов матрицСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Понятия линейной зависимости и линейной независимости определяются для строк и столбцов одинаково. Поэтому свойства, связанные с этими понятиями, сформулированные для столбцов, разумеется, справедливы и для строк. 1. Если в систему столбцов входит нулевой столбец, то она линейно зависима. 2. Если в системе столбцов имеется два равных столбца, то она линейно зависима. 3. Если в системе столбцов имеется два пропорциональных столбца 4. Система из 5. Любые столбцы, входящие в линейно независимую систему, образуют линейно независимую подсистему. 6. Система столбцов, содержащая линейно зависимую подсистему, линейно зависима. 7. Если система столбцов Докажем, например, последнее свойство. Так как система столбцов
В этом равенстве Значит, нетривиальная линейная комбинация столбцов
последовательно, линейная комбинация столбцов Пример 3.2. Доказать, что два ненулевых столбца Решение. В самом деле, если столбцы
Наоборот, если Пример 3.3. Рассмотреть всевозможные системы, образованные из столбцов
Рассмотрим системы, содержащие по два столбца:
– система – каждая из пяти систем Рассмотрим системы, содержащие три столбца: – каждая из шести систем – системы – системы Наконец, системы из четырех или из пяти столбцов линейно зависимы (по свойству 6).
Ранг матрицы В этом разделе рассмотрим еще одну важную числовую характиристику матрицы, связанную с тем, насколько ее строки (столбцы) зависят друг от друга. Определение 14.10 Пусть дана матрица Пример 14.9 Пусть Минором первого порядка является любой элемент матрицы. Так 2, Миноры второго порядка: 1. возьмем строки 1, 2, столбцы 1, 2, получим минор 2. возьмем строки 1, 3, столбцы 2, 4, получим минор 3. возьмем строки 2, 3, столбцы 1, 4, получим минор Миноры третьего порядка:
строки здесь можно выбрать только одним способом, 1. возьмем столбцы 1, 3, 4, получим минор 2. возьмем столбцы 1, 2, 3, получим минор
Предложение 14.23 Если все миноры матрицы Доказательство. Возьмем произвольный минор порядка
Определение 14.11 Рангом матрицы Единое, стандартное, обозначение ранга матрицы отсутствует. Следуя учебнику [1], мы будем обозначать его Пример 14.10 Матрица Ранг матрицы Ранг невырожденной квадратной матрицы порядка Предложение 14.24 При транспонировании матрицы ее ранг не меняется, то есть Доказательство. Транспонированный минор исходной матрицы
Определение 14.12 Пусть ранг матрицы равен Пример 14.11 Пусть Базисным минором является также минор, расположенный, скажем, в первой и третьей строках, первом и третьем столбцах: Минор в первой и второй строках, втором и третьем столбцах Так как столбцы (строки) матрицы можно складывать, умножать на числа, образовывать линейные комбинации, то можно ввести определения линейной зависимости и линейной независимости системы столбцов (строк) матрицы. Эти определения аналогичны таким же определениям 10.14, 10.15 для векторов. Определение 14.13 Система столбцов (строк) называется линейно зависимой, если существует такой набор коэффициентов, из которых хотя бы один отличен от нуля, что линейная комбинация столбцов (строк) с этими коэффициентами будет равна нулю. Определение 14.14 Система столбцов (строк) является линейно независимой, если из равенства нулю линейной комбинации этих столбцов (строк) следует, что все коэффициенты этой линейной комбинации равны нулю.
Верно также следующеее предложение, аналогичное предложению 10.6. Предложение 14.25 Система столбцов (строк) является линейно зависимой тогда и только тогда, когда один из столбцов (одна из строк) является линейной комбинацией других столбцов (строк) этой системы. Сформулируем теорему, которая называется теорема о базисном миноре. Теорема 14.2 Любой столбец матрицы является линейной комбинацией столбцов, проходящих через базисный минор. Доказательство можно найти в учебниках по линейной алгебре, например, в [1], [3]. Предложение 14.26 Ранг матрицы равен максимальному числу ее столбцов, образующих линейно независимую систему. Доказательство. Пусть ранг матрицы Предположим, что Предложение 14.27 Ранг матрицы равен максимальному числу ее строк, образующих линейно независимую систему. Доказательство. По предложению 14.24 ранг матрицы при транспонировании не меняется. Строки матрицы становятся ее столбцами. Максимальное число новых столбцов транспонированной матрицы, (бывших строк исходной) образующих линейно независимую систему, равно рангу матрицы.
Предложение 14.28 Если определитель матрицы равен нулю, то один из его столбцов (одна из строк) является линейной комбинацией остальных столбцов (строк).
Доказательство. Пусть порядок матрицы
Результаты предложений 14.15, 14.18 и 14.28 дают следующую теорему. Теорема 14.3 Определитель матрицы равен нулю тогда и только тогда, когда один из ее столбцов (одна из строк) является линейной комбинацией остальных столбцов (строк). Нахождение ранга матрицы с помощью вычисления всех ее миноров требует слишком большой вычислительной работы. (Читатель может проверить, что в квадратной матрице четвертого порядка 36 миноров второго порядка.) Поэтому для нахождения ранга применяется другой алгоритм. Для его описания потребуется ряд дополнительных сведений. Определение 14.15 Назовем элементарными преобразованиями матрицследующие действия над ними: 1) перестановка строк или столбцов; Предложение 14.29 При элементарных преобразованиях ранг матрицы не меняется. Доказательство. Пусть ранг матрицы Рассмотрим перестановку строк. Пусть Рассмотрим умножение строки на число Пусть к Если через минор Пусть через минор
Итак, в матрице Алгоритм вычисления ранга матрицы похож на алгоритм вычисления определителя и заключается в том, что с помощью элементарных преобразований матрица приводится к простому виду, для которого найти ранг не представляет труда. Так как при каждом преобразовании ранг не менялся, то, вычислив ранг преобразованной матрицы, мы тем самым находим ранг исходной матрицы.
|
|||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 1707; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.134.108.150 (0.012 с.) |

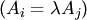 , то она линейно зависима.
, то она линейно зависима. столбцов линейно зависима тогда и только тогда, когда хотя бы один из столбцов есть линейная комбинация остальных.
столбцов линейно зависима тогда и только тогда, когда хотя бы один из столбцов есть линейная комбинация остальных. — линейно независима, а после присоединения к ней столбца
— линейно независима, а после присоединения к ней столбца  — оказывается линейно зависимой, то столбец
— оказывается линейно зависимой, то столбец  линейно зависима, то существуют числа
линейно зависима, то существуют числа  не все равные 0, что
не все равные 0, что
 . В самом деле, если
. В самом деле, если  , то
, то
 и тогда
и тогда 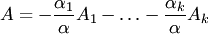 , т.е. столбец
, т.е. столбец 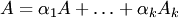 и
и  , причем не все коэффициенты разложений соответственно равны между собой (например,
, причем не все коэффициенты разложений соответственно равны между собой (например,  ). Тогда из равенства
). Тогда из равенства получаем (\alpha_1-\beta_1)A_1+\ldots+(\alpha_k-\beta_k)A_k=o
получаем (\alpha_1-\beta_1)A_1+\ldots+(\alpha_k-\beta_k)A_k=o ), то эта комбинация нетривиальная, что противоречит условию линейной независимости столбцов
), то эта комбинация нетривиальная, что противоречит условию линейной независимости столбцов  и
и  линейно зависимы тогда и только тогда, когда они пропорциональны, т.е.
линейно зависимы тогда и только тогда, когда они пропорциональны, т.е.  .
.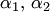 , не равные нулю одновременно, что
, не равные нулю одновременно, что 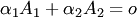 . Причем в этом равенстве
. Причем в этом равенстве  . Действительно, предположив, что
. Действительно, предположив, что 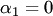 , получим противоречие
, получим противоречие  , поскольку
, поскольку 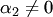 и столбец
и столбец  такое, что
такое, что  . Получили нетривиальную линейную комбинацию столбцов, равную нулевому столбцу. Значит, столбцы линейно зависимы.
. Получили нетривиальную линейную комбинацию столбцов, равную нулевому столбцу. Значит, столбцы линейно зависимы. , линейно независимы, а система, состоящая из одного нулевого столбца
, линейно независимы, а система, состоящая из одного нулевого столбца  и
и  линейно зависима, так как содержит нулевой столбец
линейно зависима, так как содержит нулевой столбец  линейно зависима, так как столбцы пропорциональны (свойство 3):
линейно зависима, так как столбцы пропорциональны (свойство 3): 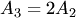 ;
; и
и  линейно независима, так как столбцы непропорциональные (см. утверждение примера 3.2).
линейно независима, так как столбцы непропорциональные (см. утверждение примера 3.2). и
и 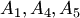 линейно зависима, так как содержит нулевой столбец
линейно зависима, так как содержит нулевой столбец  линейно зависимы, так как содержат линейно зависимую подсистему
линейно зависимы, так как содержат линейно зависимую подсистему  (свойство 6);
(свойство 6); и
и  линейно зависимы, так как последний столбец линейно выражается через остальные (свойство 4):
линейно зависимы, так как последний столбец линейно выражается через остальные (свойство 4):  и
и  соответственно.
соответственно. размеров
размеров  и число
и число  , не превосходящее наименьшего из чисел
, не превосходящее наименьшего из чисел  и
и  :
:  . Выберем произвольно
. Выберем произвольно  .
.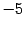 ,
,  -- миноры первого порядка.
-- миноры первого порядка. ;
; ;
;
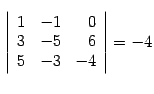 ;
; .
. , если такие существуют, тоже равны нулю.
, если такие существуют, тоже равны нулю. .
. равен 1, так как есть ненулевой минор первого порядка (элемент матрицы
равен 1, так как есть ненулевой минор первого порядка (элемент матрицы  ), а все миноры второго порядка равны нулю.
), а все миноры второго порядка равны нулю. .
. , и наоборот, любой минор
, и наоборот, любой минор 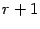 в исходной матрице равны нулю, то все миноры того же порядка в
в исходной матрице равны нулю, то все миноры того же порядка в  в исходной матрице отличен от нуля, то в
в исходной матрице отличен от нуля, то в  . Определитель матрицы
. Определитель матрицы  . Следовательно, ранг матрицы равен двум, и рассмотренный минор является базисным.
. Следовательно, ранг матрицы равен двум, и рассмотренный минор является базисным.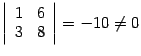 . Базисным будет минор во второй и третьей строках, первом и третьем столбцах:
. Базисным будет минор во второй и третьей строках, первом и третьем столбцах:  .
. равен нулю и поэтому не будет базисным. Читатель может самостоятельно проверить, какие еще миноры второго порядка будут базисными, а какие нет.
равен нулю и поэтому не будет базисным. Читатель может самостоятельно проверить, какие еще миноры второго порядка будут базисными, а какие нет. . Все миноры матрицы
. Все миноры матрицы  . Следовательно, система из
. Следовательно, система из  -- матрица, получившаяся в результате выполнения элементарного преобразования.
-- матрица, получившаяся в результате выполнения элементарного преобразования. -- минор матрицы
-- минор матрицы  , который или совпадает с
, который или совпадает с  матрицы
матрицы  .
. , отличное от нуля. Минору
, отличное от нуля. Минору  . Во всех случаях или
. Во всех случаях или  -ой строке матрицы
-ой строке матрицы  -ая строка, умноженная на число
-ая строка, умноженная на число  . Рассмотрим миноры порядка
. Рассмотрим миноры порядка  . Следовательно,
. Следовательно,  .
. , где
, где  -- минор порядка
-- минор порядка  " связан с возможным изменением порядка строк. Так как все миноры порядка
" связан с возможным изменением порядка строк. Так как все миноры порядка  , то есть при выполнении элементарного преобразования третьего типа ранг не может повыситься. Предположим, что
, то есть при выполнении элементарного преобразования третьего типа ранг не может повыситься. Предположим, что  , и
, и  . Тогда в матрице
. Тогда в матрице  . В результате получим исходную матрицу
. В результате получим исходную матрицу  . Получили противоречие:
. Получили противоречие:  . Предположение
. Предположение 


