
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные алгебраические структуры: векторные (линейные) пространства.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Определение. Пусть А и К – произвольные непустые множества. Другими словами, каждой паре элементов Пример 1. Пусть Пример 2. Пусть Определение. Пусть
Множество 1. Закон ассоциативности сложения:
2. Существование нулевого вектора:
3. Существование противоположного вектора:
4. Закон коммутативности сложения:
5. Закон ассоциативности умножения вектора на скаляр:
6. Закон дистрибутивности умножения вектора на скаляр относительносложения векторов:
7. Закон дистрибутивности умножения вектора на скаляр относительносложения скаляров:
8. Определение. Векторное пространство Теорема. (Простейшие свойства векторных пространств.) 1. В векторном пространстве существует единственный нулевой вектор. 2. В векторном пространстве любой вектор имеет единственный противоположный ему. 3. 4. Доказательство. Векторное пространство относительно сложенияобразует абелевую группу (аксиомы 1 – 4) откуда и следуют сразу же первые два утверждения теоремы. 3) а) Сначала мы докажем, что произведение нулевого скаляра на любой вектор равен нулевому вектору. Пусть
Применяя закон сокращения, получаем б) Теперь докажем утверждение 4): Пусть
Отсюда сразу же следует, что вектор в) Пусть теперь
г) Пусть Пример. Обозначим через
-23- Евклидово пространство
В математике термин евкли́дово простра́нство может обозначать один из двух сходных объектов: 1. Конечномерное вещественное векторное пространство
где 2. Метрическое пространство, которое является конечномерным векторным пространством
где Наглядными примерами евклидовых пространств могут служить пространства
-24- ----- -25-
|
||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 660; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 – декартово произведение этих множеств. Отображение
– декартово произведение этих множеств. Отображение 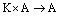 называют внешней бинарной алгебраической операцией, определенной на множестве А над множеством К.
называют внешней бинарной алгебраической операцией, определенной на множестве А над множеством К. из декартовапроизведения
из декартовапроизведения 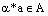 . (Обычно при написании результата алгебраическойоперации элемент
. (Обычно при написании результата алгебраическойоперации элемент  пишется слева от элемента
пишется слева от элемента  ).
).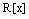 – множество многочленов от одной переменной х с действительными коэффициентами,
– множество многочленов от одной переменной х с действительными коэффициентами,  – поле действительных чисел. Тогда операция умножения многочлена на число является внешнейалгебраической операцией на множестве многочленов:
– поле действительных чисел. Тогда операция умножения многочлена на число является внешнейалгебраической операцией на множестве многочленов:  , т.е. в результате опять получается многочлен с действительными коэффициентами.
, т.е. в результате опять получается многочлен с действительными коэффициентами. – множество всех векторов как направленных отрезков. Тогда умножение вектора на число есть внешняя алгебраическая операция на множестве
– множество всех векторов как направленных отрезков. Тогда умножение вектора на число есть внешняя алгебраическая операция на множестве  , так как в результате получается вектор (направленный отрезок).
, так как в результате получается вектор (направленный отрезок). - произвольное множество, элементы которого мы будем называть векторами, К - поле, элементы которого мы будем называть скалярами. Пусть на множестве
- произвольное множество, элементы которого мы будем называть векторами, К - поле, элементы которого мы будем называть скалярами. Пусть на множестве  ;
; .
. .
. .
. .
. .
. .
. .
. .
. , где 1 - это единица поля К.
, где 1 - это единица поля К. называется вещественным векторным пространством.
называется вещественным векторным пространством. или х = 0.
или х = 0. .
. . Тогда, применяя аксиомывекторного пространства, получаем:
. Тогда, применяя аксиомывекторного пространства, получаем: .
. .
. – произвольный вектор. Тогда
– произвольный вектор. Тогда .
. является противоположным вектору х.
является противоположным вектору х. . Тогда, применяя аксиомы векторного пространства,
. Тогда, применяя аксиомы векторного пространства,  получаем:
получаем:
 .
. и допустим, что
и допустим, что 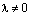 . Так как
. Так как  , где К – поле, то существует
, где К – поле, то существует  . Умножим равенство
. Умножим равенство  :
:  , откуда следует
, откуда следует  ,
,  и окончательно
и окончательно  Править
Править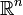 с введённой на нём нормой
с введённой на нём нормой
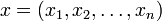 . Также назывется конечномерным гильбертовым пространством
. Также назывется конечномерным гильбертовым пространством

 размерности n = 1 (вещественная прямая) и
размерности n = 1 (вещественная прямая) и  размерности n = 2 (комплексная плоскость или евклидова плоскость).
размерности n = 2 (комплексная плоскость или евклидова плоскость).


