
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Смешанное произведение векторов.Содержание книги Поиск на нашем сайте Определение. Смешанным произведением упорядоченной тройки векторов называется скалярное произведение первого вектора навекторное произведение второго вектора на третий и обозначается . Теорема. (Геометрический смысл смешанного произведения.) 1) Модуль смешанного произведения трех векторов численно равен объему параллелепипеда, построенного на трех данных векторах, как на его ребрах: . 2), если тройка – правоориентированная и в противном случае. Доказательство. 1) Обозначим через объем параллелепипеда, построенного на данных векторах, как на его ребрах.
рис.3. Объем параллелепипеда V равен произведению площади основания S на высоту Н:. Площадь основания S численно равна модулю векторногопроизведения:, а высота Н равна модулю проекции вектора . Отсюда получаем: , ч.т.д. 2) Так как , где, то знак смешанного произведениязависит от угла. Если он острый, то смешанное произведение и, если угол – тупой. А это зависит, в свою очередь, от ориентации тройки векторов. На рисунке 3 изображена правая тройка векторов. Если смотреть со стороны третьего вектора Теорема доказана. Будем говорить, что тройки векторов и получились из тройки с помощью круговой перестановки векторов. В первом случае третий вектор Если же в тройке векторов меняются местами только два вектора, а один из векторов остается на своем месте, то такую перестановку мы будем называть не круговой перестановкой (или транспозицией). Так тройки,, получаются из тройки транспозицией векторов. Так, например, в тройке остался на третьем месте вектор Любую тройку векторов можно упорядочить 6-ю способами. Из них три тройки будут правыми и три тройки будут левыми. Если тройка правая (как на рис.3), то правыми будут и тройки полученные из нее круговой перестановкой: и. В то же время, тройка будет левой и левой же будут тройки, полученные из нее круговой перестановкой: и. Лемма. Круговая перестановка в тройке векторов не изменяет ее ориентации, а транспозиция векторов изменяет ориентацию тройки на противоположную. Доказательство проведите самостоятельно с использованием соответствующих картинок. 1); 2); 3). Доказательство. 1) По модулю все эти смешанные произведения равны друг другу, т.к. параллелепипед, построенный на данных трех векторах, как его ребрах, не зависит от того, в каком порядке мы записываем его ребра и, соответственно, не изменяется его объем. 2) Знак смешанного произведения упорядоченной тройки векторов зависит от ее ориентации, которая не меняется при круговой перестановке и меняется при транспозиции, откуда и следуют доказываемые равенства. 3) Воспользуемся уже доказанным равенством, определением смешанного произведения и свойством коммутативности скалярногопроизведения: . Следствие доказано.
-26-
Коллинеарные и компланарные векторы Определение. Векторы называются коллинеарными, если они расположены на одной или параллельных прямых. Нулевой вектор коллинеарен любому вектору. Определение. Векторы называются компланарными, если существует плоскость, которой они параллельны. Коллинеарные векторы всегда компланарны, но не все компланарные векторы коллинеарны. Определение. Векторы называются равными, если они коллинеарны, одинаково направлены и имеют одинаковые модули. Всякие векторы можно привести к общему началу, т.е. построить векторы, соответственно равные данным и имеющие общее начало. Из определения равенства векторов следует, что любой вектор имеет бесконечно много векторов, равных ему. -27- Общее уравнение прямой Общее уравнение прямой линии на плоскости в декартовых координатах:
где A, B и C — произвольные постоянные, причем постоянные A и B не равны нулю одновременно. Вектор с координатами (A, B)называется нормальным вектором и он перпендикулярен прямой. Вектор с координатами (-B,A) или (B,-A) называется направляющим вектором. При C = 0 прямая проходит через начало координат. Также уравнение можно переписать в виде:
|
||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 415; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.01 с.) |

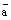 на вектор:
на вектор: , то кратчайший поворот первого вектора
, то кратчайший поворот первого вектора  осуществляется против часовой стрелки. В этом случае угол – острый и. Если же тройка – левая, то конец вектора
осуществляется против часовой стрелки. В этом случае угол – острый и. Если же тройка – левая, то конец вектора  и
и  . Отложим от произвольной точки O векторы
. Отложим от произвольной точки O векторы  и
и  . Углом между векторами
. Углом между векторами  . Обозначается
. Обозначается  .
Рассмотрим ось l и отложим на ней единичный вектор
.
Рассмотрим ось l и отложим на ней единичный вектор  (т.е. вектор, длина которого равна единице).
Под углом между вектором
(т.е. вектор, длина которого равна единице).
Под углом между вектором 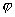 между векторами
между векторами  – вектор.
Обозначим через A1 и B1 проекции на ось l соответственно точек A и B. Предположим, что A1 имеет координату x1, а B1 – координату x2 на оси l.
Тогда проекцией вектора
– вектор.
Обозначим через A1 и B1 проекции на ось l соответственно точек A и B. Предположим, что A1 имеет координату x1, а B1 – координату x2 на оси l.
Тогда проекцией вектора  на ось l называется разность x1 – x2 между координатами проекций конца и начала вектора
на ось l называется разность x1 – x2 между координатами проекций конца и начала вектора  .
Ясно, что если угол между вектором
.
Ясно, что если угол между вектором  Доказательство. Ясно, что проекция вектора не изменится при его параллельном переносе, поэтому достаточно рассмотреть случай, когда начало вектора совпадает с началом отсчёта O оси l. Так как координата проекции начала равна нулю, то обозначим
Доказательство. Ясно, что проекция вектора не изменится при его параллельном переносе, поэтому достаточно рассмотреть случай, когда начало вектора совпадает с началом отсчёта O оси l. Так как координата проекции начала равна нулю, то обозначим 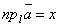 .
1. Если угол φ острый, то из прямоугольного
.
1. Если угол φ острый, то из прямоугольного  получаем
получаем  . Откуда
. Откуда  или
или  2. Если угол φ тупой, то x < 0,
2. Если угол φ тупой, то x < 0,  . Тогда из
. Тогда из 
 или
или  . Т.е.
. Т.е.  .
2. Проекция суммы двух векторов на ось равна сумме проекций векторов на ту же ось:
.
2. Проекция суммы двух векторов на ось равна сумме проекций векторов на ту же ось: 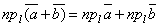 .
Доказательство. Пусть
.
Доказательство. Пусть  . Обозначим через x1, x2 и x3 координаты проекций A1, B1, C1 на ось l точек A, B и C. Тогда
. Обозначим через x1, x2 и x3 координаты проекций A1, B1, C1 на ось l точек A, B и C. Тогда  . Но
. Но  .
Это свойство можно обобщить на случай любого числа слагаемых.
3. Если вектор
.
Это свойство можно обобщить на случай любого числа слагаемых.
3. Если вектор 
 .
Доказательство. Пусть угол между вектором
.
Доказательство. Пусть угол между вектором  .
Если λ > 0, то вектор
.
Если λ > 0, то вектор  имеет то же направление, что и
имеет то же направление, что и  .
Если же λ < 0, то
.
Если же λ < 0, то  .
Следствие. Проекция разности двух векторов на ось равна разности проекций этих векторов на ту же ось.
.
Следствие. Проекция разности двух векторов на ось равна разности проекций этих векторов на ту же ось.












