
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поверхности второго порядка.Содержание книги
Поиск на нашем сайте
Линейные образы. 3.1.1. Прямая на плоскости. Кривые второго порядка. 3.2.1. Окружность. Поверхности второго порядка. 3.4. Преобразование координат. 3.4.1. Преобразование координат на плоскости. 4. Комплексные числа……………………………………………………………………..20 4.1. Алгебраическая форма комплексного числа. 5. Введение в анализ………………………………………………………………………22 5.1. Функции. Общие свойства. 6. Дифференциальное исчисление…………………………………………………..28 6.1. Определение производной. 7. Интегральное исчисление……………………………………………………………34 Неопределённый интеграл. 7.1.1. Определения и свойства. Определённый интеграл. 7.2.1. Определения и свойства.
Определители (детерминанты) Обозначения определителя матрицы А: D, det A, Определитель второго порядка: Определитель третьего порядка:
Разложение определителя n-го порядка по i-й строке:
Разложение определителя n-го порядка по j-ому столбцу:
Матрицы Равенство матриц: Квадратная матрица порядка n: Сложение матриц: Свойства сложения матриц: 1) ассоциативность: 2) коммутативность: Умножение матрицы на число: Умножение матриц: Свойства умножения матриц:
Транспонирование матрицы:
Свойство транспонирования произведения матриц: Невырожденная (неособая) матрица: Обратная матрица для невырожденной матрицы A: Свойства обратной матрицы: 1) 2) Виды матриц: единичная матрица: симметрическая матрица: ортогональная матрица: A - невырождена и кососимметрическая матрица: матрица-строка: матрица-столбец: Ранг матрицы Системы линейных уравнений
Матричный вид:
Совместность системы: Формулы Крамера (n=m):
Однородная система (B=0):
Линейные образы 3.1.1. Прямая на плоскости
Виды уравнений
Формулы для вычисления угла между двумя прямыми на плоскости:
где
Условия параллельности двух прямых на плоскости:
Условия перпендикулярности двух прямых на плоскости:
3.1.2. Плоскость в пространстве Виды уравнений
Выражение направляющих косинусов через координаты нормального вектора:
Формулы для вычисления угла между двумя плоскостями:
где Условие параллельности двух плоскостей:
Условие перпендикулярности двух плоскостей: n1 3.1.3. Прямая в пространстве Виды уравнений
Формулы для вычисления угла между двумя прямыми в пространстве:
где Условие параллельности двух прямых в пространстве:
Условие ортогональности двух прямых в пространстве: q1
Кривые второго порядка Общее уравнение кривой второго порядка:
3.2.1. Окружность
3.2.2. Эллипс
3.2.3. Гипербола
3.2.4. Парабола
3.3. Поверхности второго порядка
3.4. Преобразование координат 3.4.1. Преобразование координат на плоскости Преобразование декартовой прямоугольной системы координат.
где координаты точки Mв старой системе координат: координаты точки M в новой системе координат: координаты нового начала координат:
где координаты точки M в старой системе координат: координаты точки M в новой системе координат: угол поворота: j.
3.4.2. Преобразование координат в пространстве Переход от декартовых координат
Переход от декартовых координат
Мнимая единица Функции. Общие свойства Числовая функция определена на множестве D действительных чисел, если каждому значению переменной Аналитическое представление функции: в явном виде: в неявном виде: в параметрической форме: разными формулами в области определения (a,c]: Четная функция: Нечетная функция: Периодическая функция: Теория пределов Пределом функции Обозначение: Пределом функции
Обозначение: Формула для вычисления предела элементарной функции Бесконечно малая величина при Бесконечно большая величина при Первый замечательный предел: Следствия: Второй замечательный предел: Следствия: Эквивалентные бесконечно малые величиныпри x ~ sinx ~ tgx ~ arcsinx ~ arctgx ~ ex-1 ~ ln(1+x). Виды неопределенностей:
Непрерывность функции Функция Эквивалентные условия:
Классификация точек разрыва: разрыв I рода: - устранимый – односторонние пределы существуют и равны; - неустранимый (скачок) – односторонние пределы не равны; разрыв II рода: предел функции в точке не существует.
Определение производной Пусть Производная функции в точке x 0 и ее обозначения: Гиперболические функции
Обратные гиперболические функции
Графики гиперболических функций:
Исследование функций План полного исследования функции:
- найти область определения и область значений; - выяснить общие свойства: четность(нечетность), периодичность; - найти точки пересечения с осями координат; - определить участки знакопостоянства. 2. Исследование с помощью предела: - найти точки разрыва и выяснить их характер; - найти область непрерывности; - найти вертикальные и наклонные асимптоты. 3. Исследование с помощью - найти критические точки; - определить интервалы возрастания и убывания функции; - определить экстремумы. 4. Исследование с помощью - найти точки, в которых - найти участки выпуклости и вогнутости; - определить точки перегиба. 5. Построение графика функции. Рекомендации по применению плана исследования функции:
Неопределенный интеграл 7.1.1. Определения и свойства Функция Неопределенным интегралом от функции f(x) называется совокупность всех первообразных для этой функции. Обозначение: Свойства неопределенного интеграла
4а. Неопределенный интеграл от суммы (разности) двух функций: 4б. Вынесение постоянного множителя за знак неопределенного интеграла: 7.1.2. Основные методы интегрирования
а) замена
б) замена
7.1.3. Таблица интегралов
Определенный интеграл 7.2.1. Определения и свойства
Свойства определенного интеграла
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-25; просмотров: 196; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.155.227 (0.014 с.) |

 .
. .
.
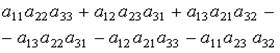

 -алгебраическое дополнение элемента
-алгебраическое дополнение элемента  ,
,  ,
, -минор элемента
-минор элемента  , если эти матрицы одного размера и
, если эти матрицы одного размера и  .
. .
. , где
, где  .
. ;
; ;
; .
. .
. ;
; .
. .
. .
. .
. .
. ;
; .
.



 ;
;
 .
. - наибольший порядок её ненулевого минора или наибольшее число линейно независимых строк (столбцов) матрицы.
- наибольший порядок её ненулевого минора или наибольшее число линейно независимых строк (столбцов) матрицы.
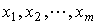 - неизвестные;
aij –коэффициент в i-ом уравнении при j-ом неизвестном;
- неизвестные;
aij –коэффициент в i-ом уравнении при j-ом неизвестном;
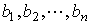 - свободные члены.
- свободные члены.
 ,
,  - матрица системы,
- матрица системы,

 , где
, где  - расширенная матрица системы (теорема Кронекера-Капелли).
- расширенная матрица системы (теорема Кронекера-Капелли). ,
, - определитель матрицы системы;
- определитель матрицы системы; -определитель, полученный при замене i-го столбца матрица A на столбец В.
-определитель, полученный при замене i-го столбца матрица A на столбец В.
 , то система им
, то система им  еет только нулевое решение.
Если
еет только нулевое решение.
Если 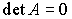 , то существуют ненулевые решения.
, то существуют ненулевые решения.



 a
a  b
b

 , e
, e 
 a| | b
a| | b


 только при условии
только при условии  .
.

 ,
,  ,
,  - координаты фиксированных точек на прямой;
k - угловой коэффициент прямой;
a - отрезок, отсекаемый прямой на оси х;
b - отрезок, отсекаемый прямой на оси y;
q=(l,m) - направляющий вектор прямой
- координаты фиксированных точек на прямой;
k - угловой коэффициент прямой;
a - отрезок, отсекаемый прямой на оси х;
b - отрезок, отсекаемый прямой на оси y;
q=(l,m) - направляющий вектор прямой



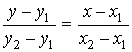


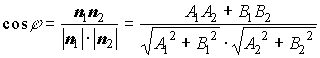 ;
;  ,
, и
и  -нормальный и направляющий векторы первой прямой;
-нормальный и направляющий векторы первой прямой; и
и  - нормальный и направляющий векторы второй прямой.
- нормальный и направляющий векторы второй прямой. ;
;  ;
; 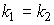 , где
, где  и
и  - угловые коэффициенты прямых.
- угловые коэффициенты прямых.  n1
n1 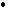 n2=0 или A1A2+B1B2=0;
n2=0 или A1A2+B1B2=0; 

 - нормальный вектор плоскости;
- нормальный вектор плоскости;

 - координаты фиксированных точек на плоскости;
a,b,c – отрезки, отсекаемые плоскостью на осях координат;
- координаты фиксированных точек на плоскости;
a,b,c – отрезки, отсекаемые плоскостью на осях координат;
 - направляющие косинусы нормального вектора плоскости;
p - длина перпендикуляра, опущенного из начала координат на плоскость
- направляющие косинусы нормального вектора плоскости;
p - длина перпендикуляра, опущенного из начала координат на плоскость





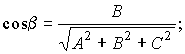
 .
.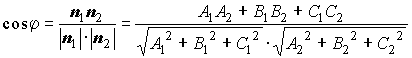 ;
; и
и  -нормальные векторы плоскостей.
-нормальные векторы плоскостей. .
.
 и
и  - нормальные векторы плоскостей;
- нормальные векторы плоскостей;
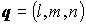 - направляющий вектор прямой;
- направляющий вектор прямой;
 ,
,  ,
,  - координаты фиксированных точек на прямой
- координаты фиксированных точек на прямой



 ,
, и
и  - направляющие векторы прямых.
- направляющие векторы прямых. .
. .
. .
Радиус окружности: a.
.
Радиус окружности: a.

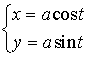

 с центром в точке с координатами
с центром в точке с координатами  :
:

 .
Полуоси эллипса:
.
Полуоси эллипса:  . Фокусное расстояние: c. Фокусы:
. Фокусное расстояние: c. Фокусы:  и
и  , где
, где  .
.
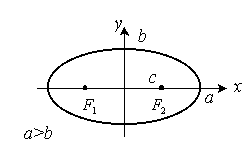
 ,
,  .
.
 .
.
 и
и  , где
, где  .
.

 ;
; 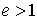 ;
;
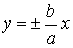

 ,
Параметр: p. Фокус:
,
Параметр: p. Фокус:  ; директриса:
; директриса:  .
.



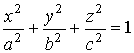 .
.
 - полуоси
- полуоси


 -действитель-ные полуоси,
-действитель-ные полуоси,
 - мнимая полуось
- мнимая полуось


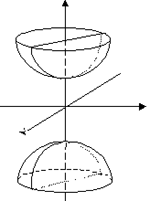

 - полуоси
- полуоси
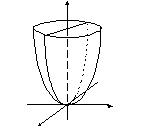


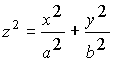







 ,
,

 ;
;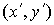 ;
; .
.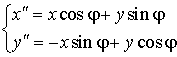 ,
,

 ;
; к полярным координатам
к полярным координатам  и обратно.
и обратно.  ;
;
 ;
;  ;
; 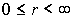 ;
; 

 к цилиндрическим координатам
к цилиндрическим координатам  и обратно:
и обратно:

 к сферическим координатам
к сферическим координатам  и обратно:
и обратно:
 ,
,
 ;
; 

 .
. поставлено в соответствие некоторое вполне определенное действительное значение переменной y, где D – область определения функции.
поставлено в соответствие некоторое вполне определенное действительное значение переменной y, где D – область определения функции. ;
;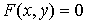 ;
; ;
; .
. .
. .
. , где T – период функции,
, где T – период функции,  .
. при
при  называется число b, если для любого
называется число b, если для любого  (e -сколь угодно малое положительное число) можно найти такое значение аргумента
(e -сколь угодно малое положительное число) можно найти такое значение аргумента  , начиная с которого выполняется неравенство
, начиная с которого выполняется неравенство  .
. .
. при
при  называется число b, если для любого
называется число b, если для любого  выполняется неравенство
выполняется неравенство  .
. , где
, где  :
:  .
. есть функция
есть функция 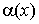 такая, что
такая, что  .
. есть функция
есть функция  такая, что
такая, что  .
. .
. ;
;  ;
;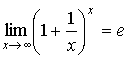 , где e=2,71828…
, где e=2,71828… ;
; 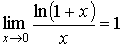 ;
;  ;
;  .
.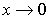 :
:







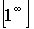





 непрерывна в точке
непрерывна в точке  , если предел функции при стремлении аргумента к a, существует и равен значению функции в этой точке.
, если предел функции при стремлении аргумента к a, существует и равен значению функции в этой точке. ;
;  , где
, где  ;
; ;
; .
.  - определена и непрерывна в окрестности x0
- определена и непрерывна в окрестности x0 




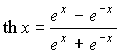












 :
: :
: или не существует;
или не существует; называется первообразной для
называется первообразной для  .
. , где
, где  - произвольная постоянная.
- произвольная постоянная. .
.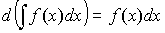 .
. .
. ;
;  ;
;
 в интеграле
в интеграле  :
: 
 где
где  - функция, интегрируемая легче, чем исходная;
- функция, интегрируемая легче, чем исходная;  - функция, обратная функции
- функция, обратная функции 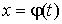 ;
;  - первообразная функции
- первообразная функции  ;
; в интеграле вида
в интеграле вида  :
:
 ;
;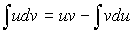 .
.

 ,
, 

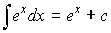

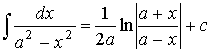







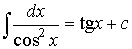

 , где
, где 



