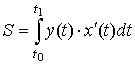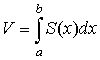Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Производные высших порядков и формула ТейлораСодержание книги
Поиск на нашем сайте
Производная второго порядка функции y=f(x): Производная n-го порядка (n-ая производная) функции y=f(x): Формула Тейлора:
где Формула Маклорена (a=0):
Исследование функций План полного исследования функции:
- найти область определения и область значений; - выяснить общие свойства: четность(нечетность), периодичность; - найти точки пересечения с осями координат; - определить участки знакопостоянства. 2. Исследование с помощью предела: - найти точки разрыва и выяснить их характер; - найти область непрерывности; - найти вертикальные и наклонные асимптоты. 3. Исследование с помощью - найти критические точки; - определить интервалы возрастания и убывания функции; - определить экстремумы. 4. Исследование с помощью - найти точки, в которых - найти участки выпуклости и вогнутости; - определить точки перегиба. 5. Построение графика функции. Рекомендации по применению плана исследования функции:
Неопределенный интеграл 7.1.1. Определения и свойства Функция Неопределенным интегралом от функции f(x) называется совокупность всех первообразных для этой функции. Обозначение: Свойства неопределенного интеграла
4а. Неопределенный интеграл от суммы (разности) двух функций: 4б. Вынесение постоянного множителя за знак неопределенного интеграла:
7.1.2. Основные методы интегрирования
а) замена
б) замена
7.1.3. Таблица интегралов
Определенный интеграл 7.2.1. Определения и свойства
Свойства определенного интеграла
а)
б) 7.2.2. Приложения определенного интеграла
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-25; просмотров: 232; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.200.142 (0.007 с.) |



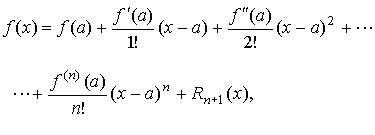
 - остаточный член в форме Лагранжа.
- остаточный член в форме Лагранжа.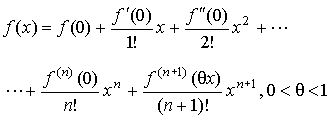
 :
: :
: или не существует;
или не существует; называется первообразной для
называется первообразной для  , если
, если  .
. , где
, где  - произвольная постоянная.
- произвольная постоянная. .
.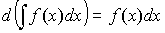 .
. .
. ;
;  ;
;
 в интеграле
в интеграле  :
: 
 где
где  - функция, интегрируемая легче, чем исходная;
- функция, интегрируемая легче, чем исходная;  - функция, обратная функции
- функция, обратная функции 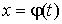 ;
;  - первообразная функции
- первообразная функции  ;
; в интеграле вида
в интеграле вида  :
:
 ;
;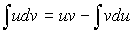 .
.

 ,
, 

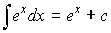

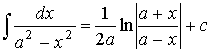







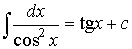

 , где
, где 
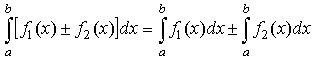 .
.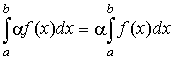 .
. .
. ,
,  , то
, то  .
.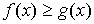 и
и  , то
, то  .
. , где
, где 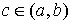 ,
,  .
. , где
, где  - первообразная для
- первообразная для  .
.
 , где
, где  ,
,  ,
,  и
и  , а
, а 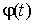 непрерывна и монотонна на
непрерывна и монотонна на 
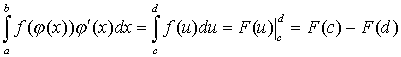 , где u=j (x), c=j (a), d=j (b).
, где u=j (x), c=j (a), d=j (b).