Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгебраическая форма комплексного числаСодержание книги
Поиск на нашем сайте
a - действительная часть комплексного числа, b - мнимая часть комплексного числа; Обозначения действительной и мнимой части: Модуль комплексного числа: Сопряжённые комплексные числа: Действия над комплексными числами в алгебраической форме
Тригонометрическая форма комплексного числа
где Показательная форма комплексного числа
Формула Эйлера: Действия над комплексными числами в тригонометрической и показательной форме
где Формула Муавра:
Функции. Общие свойства Числовая функция определена на множестве D действительных чисел, если каждому значению переменной Аналитическое представление функции: в явном виде: в неявном виде: в параметрической форме: разными формулами в области определения (a,c]: Четная функция: Нечетная функция: Периодическая функция: Основные элементарные функции
Графики основных элементарных функций:
Теория пределов Пределом функции Обозначение: Пределом функции Обозначение: Формула для вычисления предела элементарной функции Бесконечно малая величина при Бесконечно большая величина при Первый замечательный предел: Следствия: Второй замечательный предел: Следствия: Эквивалентные бесконечно малые величиныпри x ~ sinx ~ tgx ~ arcsinx ~ arctgx ~ ex-1 ~ ln(1+x). Виды неопределенностей:
Непрерывность функции Функция Эквивалентные условия:
Классификация точек разрыва: разрыв I рода: - устранимый – односторонние пределы существуют и равны; - неустранимый (скачок) – односторонние пределы не равны; разрыв II рода: предел функции в точке не существует.
Определение производной Пусть Производная функции в точке x 0 и ее обозначения: Основные правила дифференцирования
Производные основных элементарных функций
Гиперболические функции
Обратные гиперболические функции
Графики гиперболических функций:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-25; просмотров: 298; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.47.157 (0.009 с.) |

 , где a, b – действительные числа;
, где a, b – действительные числа; .
. .
. и
и  .
. ;
; ;
; .
. ,
, - аргумент комплексного числа,
- аргумент комплексного числа,  .
. .
. .
. ,
, ,
, ,
, .
. .
. поставлено в соответствие некоторое вполне определенное действительное значение переменной y, где D – область определения функции.
поставлено в соответствие некоторое вполне определенное действительное значение переменной y, где D – область определения функции. ;
;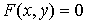 ;
; ;
; .
. .
. .
. , где T – период функции,
, где T – период функции,  .
.


 ;
;
 ;
;  ;
;
 ;
; 



 ;
; 
 ;
;  ;
;
 ;
;  .
.
 ;
;
 ;
;
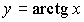 ;
;









 и косинусоида
и косинусоида 


 при
при  называется число b, если для любого
называется число b, если для любого  (e -сколь угодно малое положительное число) можно найти такое значение аргумента
(e -сколь угодно малое положительное число) можно найти такое значение аргумента  , начиная с которого выполняется неравенство
, начиная с которого выполняется неравенство  .
. .
. при
при  называется число b, если для любого
называется число b, если для любого  выполняется неравенство
выполняется неравенство  .
. , где
, где  :
:  .
. есть функция
есть функция 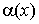 такая, что
такая, что  .
. есть функция
есть функция  такая, что
такая, что  .
. .
. ;
;  ;
;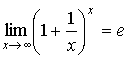 , где e=2,71828…
, где e=2,71828… ;
; 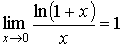 ;
;  ;
;  .
. :
:












 непрерывна в точке
непрерывна в точке  , если предел функции при стремлении аргумента к a, существует и равен значению функции в этой точке.
, если предел функции при стремлении аргумента к a, существует и равен значению функции в этой точке. ;
;  , где
, где  ;
; ;
; .
.  - определена и непрерывна в окрестности x0
- определена и непрерывна в окрестности x0 




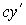





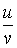


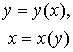









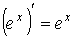


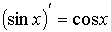 ;
;  ;
;  ;
;  ;
;
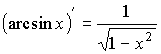 ;
;  ;
;  ;
;