
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: Построение кривых второго порядка.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Цель: Рассмотреть возможности построения кривых второго порядка в системе Mathcad Порядок выполнения работы: 1) Повторить некоторые теоретические сведения, известные из курса аналитической геометрии, необходимые для выполнения работы. 2) Рассмотреть примеры построения кривых второго порядка в Mathcad в Приложении В. 3) Выполнить задачи для самостоятельного решения по вариантам. Вариант соответствует порядковому номеру в журнале. 4) Написать отчет (в свободной форме).
Основные теоретические сведения, необходимые для выполнения лабораторной работы.
Общее уравнение кривой второго порядка относительно некоторой прямоугольной декартовой системы координат имеет вид:
где
Существует 9 кривых второго порядка на плоскости. Приведем канонические уравнения этих кривых ( 1) 2) 3) 4) 5) 6) 7) 8) 9) Чтобы определить тип кривой второго порядка достаточно вычислить знаки некоторых выражений, составленных из коэффициентов уравнения. Пусть кривая II порядка задана уравнением (3.1). Введем следующие обозначения
Числа D и В таблице 1 видно, какому сочетанию знаков определителей D и
Таблица 1
Эллипс Эллипсом называется геометрическое место точек, сумма расстояний которых до двух данных точек, называемых фокусами, есть постоянная величина 2 а, большая, чем расстояние между фокусами 2 с. Каноническое уравнение эллипса имеет вид
где
Отношение Расстояние точки М (х, y) эллипса до его фокусов (фокальные радиусы) находятся по формулам
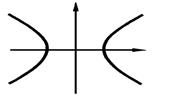
Гипербола Гиперболой называется геометрическое место точек, разность расстояний от которых до двух данных точек (фокусов) есть постоянная величина 2 а, причем 2 a <2 c, где 2 с – расстояние между фокусами. Каноническое уравнение гиперболы, симметричной относительно осей координат, имеет вид
где Параметр а называется вещественной полуосью гиперболы и представляет собой расстояние от начала координат до вершины гиперболы, параметр b называется мнимой полуосью. Эксцентриситетом гиперболы называется величина Расстояния текущей М (х,y) гиперболы до фокусов (фокальные радиусы) определяются по формулам
Прямые, заданные уравнениями
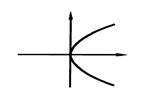
Парабола Параболой называется геометрическое место точек, одинаково удаленных от данной точки (фокуса) и данной прямой (директрисы). Каноническое уравнение параболы, проходящей через начало координат и симметричной оси Ох, имеет вид
Уравнение вида
описывает параболу, симметричную относительно оси Оу. Фокальный радиус точки М (х,y), т.е. ее расстояние до фокуса на оси Ох, находится по формуле
Парабола, ось которой параллельна оси Оу, описывается уравнением Задания для самостоятельного выполнения:
Построить кривые II порядка и определить их тип. Для эллипса найти координаты фокусов, эксцентриситет и фокальные радиусы. Для гиперболы найти координаты фокусов, эксцентриситет, фокальные радиусы и уравнения асимптоты. Для параболы найти координаты фокуса и фокальный радиус. 1 вариант а) г) ж) у 2 + 4 х = 0 з) х 2 – 4 = 0 и) у 2 + 4 = 0
к) 2 вариант а)
г)
ж) х 2 – 4 у = 0 з) у 2 – 18 = 0 и) х 2 + 10 = 0
к) 3 вариант а)
г) 5 х 2 + 10 у 2 = 0 д) х 2 – у 2 = 0 е) 10 у 2 = 0
ж) у 2 – 10 х =0 з) у 2 –16 = 0 и) у2 + 16 = 0
к) 4 вариант а) 15 х 2 +100 у 2 = 12 б)
г)
ж) к) 5 вариант а) 20 х 2 +120 у 2 = 10 б)
г)
ж) к) 6 вариант а) 15 х 2 + у 2 = 60 б)
г)
ж) к) 7 вариант а) 20 х 2 + 40 у 2 = 100 б)
г)
ж) к) 8 вариант а) 15 х 2 + 5 у 2 = 60 б)
г)
ж)
к) 9 вариант а) х 2 + 20 у 2 = 100 б)
г)
ж)
к)
10 вариант а) 5 у 2 + 20 х 2 = 60 б)
г)
ж) к) 11 вариант а) 5 х 2 + 6 у 2 = 120 б)
г)
ж) к) 12 вариант а) 15 х 2 + 16 у 2 = 80 б)
г)
ж) к) 13 вариант а) 8 х 2 + 16 у 2 = 20 б)
г)
ж) к) 14 вариант а) 18 х 2 +40 у 2 =36 б)
г)
ж) к) 15 вариант а) 15 х 2 + 45 у 2 = 100 б)
г)
ж) к) 16 вариант а) 5 х 2 + 40 у 2 = 50 б)
г)
ж) к)
|
|||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 994; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.76.151 (0.011 с.) |

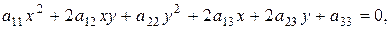 (3.1)
(3.1)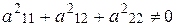
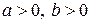 ).
). - уравнение эллипса
- уравнение эллипса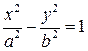 - уравнение гиперболы
- уравнение гиперболы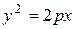 - уравнение параболы
- уравнение параболы - мнимый эллипс
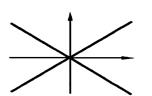
- мнимый эллипс - пара действительных пересекающихся прямых
- пара действительных пересекающихся прямых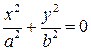 - пара мнимых пересекающихся прямых
- пара мнимых пересекающихся прямых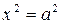 - пара действительных параллельных прямых
- пара действительных параллельных прямых - пара мнимых параллельных прямых
- пара мнимых параллельных прямых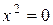 - пара действительных совпавших прямых.
- пара действительных совпавших прямых.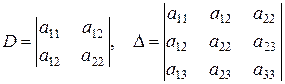
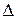 не зависят от выбора системы координат на плоскости и называются инвариантами.
не зависят от выбора системы координат на плоскости и называются инвариантами.
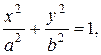
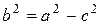 , если a>b и фокусы находятся на оси Ох. Параметры a и b называются полуосями эллипса.
, если a>b и фокусы находятся на оси Ох. Параметры a и b называются полуосями эллипса.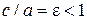 называется эксцентриситетом эллипса.
называется эксцентриситетом эллипса.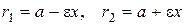 .
.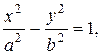
 .
. .
. .
. , являются асимптотами гиперболы.
, являются асимптотами гиперболы.
 .
. .
. б)
б) 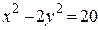 в)
в) 
 д)
д)  е) 5 у 2=0
е) 5 у 2=0
 б)
б)  в)
в) 
 д) 20 х 2 = 5 у 2 е) 150 х 2 = 0
д) 20 х 2 = 5 у 2 е) 150 х 2 = 0
 б)
б)  в) х 2 + у 2 + 1= 0
в) х 2 + у 2 + 1= 0
 в)
в) 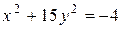
 д)
д) 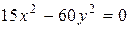 е) 20 х 2 = 0
е) 20 х 2 = 0 з) у 2 + 4 = 0 и) у 2 – 16 = 0
з) у 2 + 4 = 0 и) у 2 – 16 = 0
 в)
в) 
 д)
д)  е) 15 х 2 = 0
е) 15 х 2 = 0 з) 2 х 2 + 4 = 0 и) х 2 – 8 = 0
з) 2 х 2 + 4 = 0 и) х 2 – 8 = 0
 в)
в) 
 д)
д)  е) 100 х 2 = 0
е) 100 х 2 = 0 з) 12 у 2 + 8 = 0 и) у 2 – 12 = 0
з) 12 у 2 + 8 = 0 и) у 2 – 12 = 0
 в)
в) 
 д)
д) 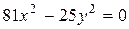 е) 64 х 2 = 0
е) 64 х 2 = 0 з) 5 у 2 + 10 = 0 и) 2 у 2 – 5 = 0
з) 5 у 2 + 10 = 0 и) 2 у 2 – 5 = 0
 в)
в) 
 д)
д)  е) 115 х 2 = 0
е) 115 х 2 = 0 з) х 2 + 3 = 0 и) 5 х 2 = 10
з) х 2 + 3 = 0 и) 5 х 2 = 10
 в)
в) 
 д)
д)  е) 22 у 2 = 0
е) 22 у 2 = 0 з) 5 у 2 +7 = 0 и) 5 у 2 =12
з) 5 у 2 +7 = 0 и) 5 у 2 =12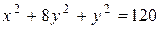
 в)
в) 
 д)
д)  е) 156 у 2 = 0
е) 156 у 2 = 0
 в)
в) 
 д)
д)  е) 1112 х 2 = 0
е) 1112 х 2 = 0
 в)
в) 
 д)
д)  е) 21 у 2 = 0
е) 21 у 2 = 0 з) 12 х 2 + 8 = 0 и) 5 х 2 = 10
з) 12 х 2 + 8 = 0 и) 5 х 2 = 10
 в)
в) 
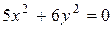 д)
д)  е) 51 х 2 = 0
е) 51 х 2 = 0 з) 5 у 2 + 6 = 0 и) 2 у 2 = 6
з) 5 у 2 + 6 = 0 и) 2 у 2 = 6
 в)
в) 
 д)
д)  з) 12 х 2 + 8 = 0 и) 3 х 2 = 8
з) 12 х 2 + 8 = 0 и) 3 х 2 = 8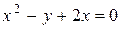
 в)
в) 
 д)
д)  е) 22 у 2 = 0
е) 22 у 2 = 0 з) 16 х 2 + 144 = 0 и) у 2 = 12
з) 16 х 2 + 144 = 0 и) у 2 = 12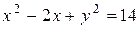
 в)
в) 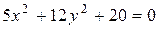
 е) 11 х 2 = 0
е) 11 х 2 = 0 з) 15 х 2 + 12 = 0 и) 16 у 2 = 8
з) 15 х 2 + 12 = 0 и) 16 у 2 = 8 .
.


