Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение поверхностей второго порядка в среде MathcadСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Построение поверхностей в Mathcad. Построение графика поверхности в системе Mathcad может осуществляться несколькими способами.
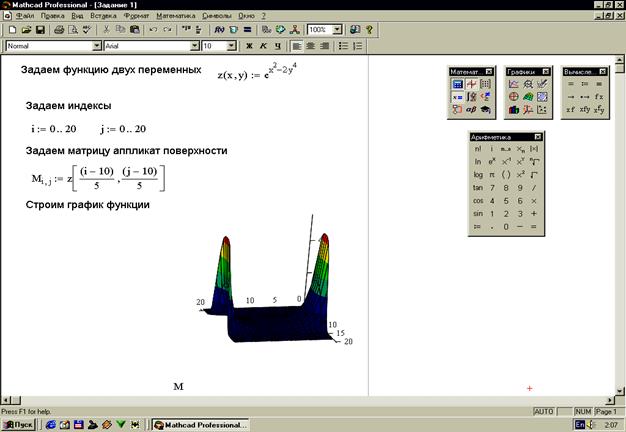
1 Построение поверхностей по матрице аппликат их точек. Поскольку элементы матрицы М – индексированные переменные с целочисленными индексами, то перед созданием матрицы требуется задать индексы в виде ранжированных переменных с целочисленными значениями, а затем из них сформировать сетку значений х и у – координат для аппликат z (x,y). Значения х и у могут быть любыми действительными числами. После указанных выше определений вводится шаблон графика (либо с помощью подменю меню Вставка, либо с помощью панели Graph). Левый верхний угол шаблона помещается в место расположения курсора. Шаблон содержит единственное место ввода – темный прямоугольник у левого нижнего угла основного шаблона. В него надо занести имя матрицы аппликат поверхности. После этого надо установить указатель мыши в стороне от графического блока и щелкнуть левой кнопкой. Следует заметить, так как график строится на основе матрицы, содержащей только координаты высот фигуры, то истинные масштабы по осям абсцисс и ординат неизвестны и на рисунках не проставляются. Однако можно выводить порядковые номера элементов матриц в заданном направлении. Необходимо следить за тем, как сформировать векторы Х и У, чтобы поверхность выглядела естественно и была видна нужная часть поверхности.
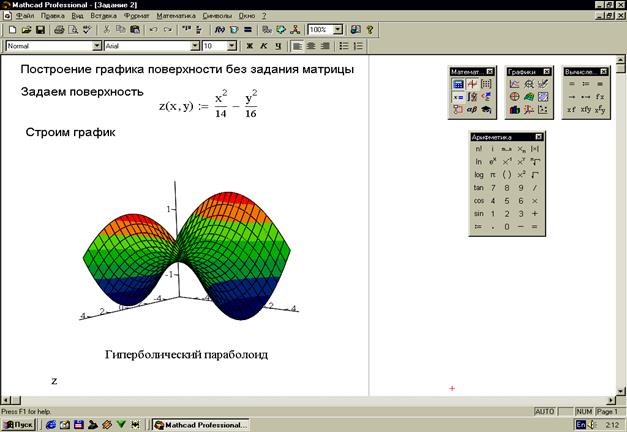
2 Построение трехмерных графиков без задания матрицы. В данном случае для построения достаточно задать функцию переменных х и у. В результате построение графиков поверхностей выполняется также просто, как и построение двухмерных графиков. Недостатками такого построения являются неопределенность в масштабировании и то, что не все поверхности второго порядка можно построить таким образом. Форматирование трехмерных графиков. Принцип форматирования трехмерных графиков такой же, как и форматирования двухмерных графиков. Отличие состоит лишь в большем количестве параметров форматирования. Задание 1. Построить поверхность по матрице аппликат ее точек (рисунок 30). Задание 2. Построить поверхность без задания матрицы (рисунок 31).
Рисунок 30
Рисунок 31
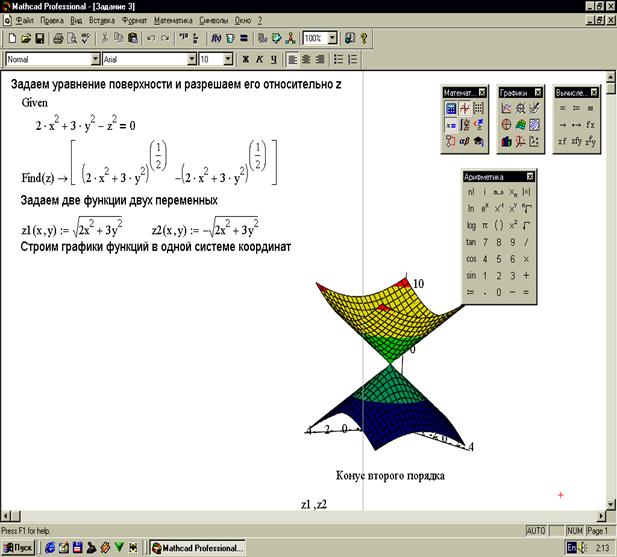
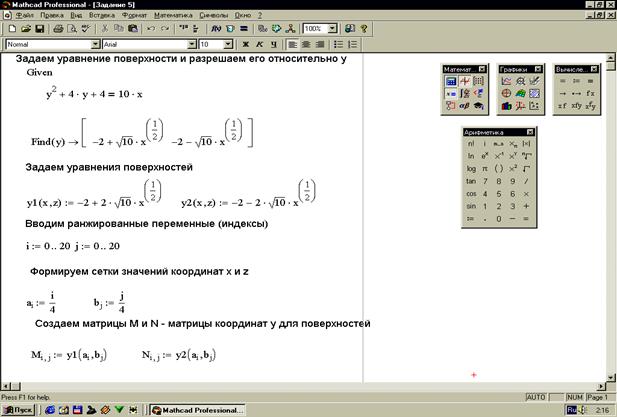
Уравнение поверхности не всегда задается в явном виде. Для того чтобы построить поверхность заданную неявно необходимо сначала уравнение данной поверхности разрешить относительно какой-либо переменной, а затем строить поверхности по полученным уравнениям. Задание 3. Построить поверхность, заданную уравнением Задание 4. Построить поверхность, заданную уравнением Возможности системы Mathcad позволяют строить пересекающиеся поверхности в одной системе координат. Задание 5. Построить поверхности В пакете Mathcad также возможно построение поверхностей, заданных в параметрической форме. Примеры таких построений приведены на рисунках 36 и 37.
Рисунок 32
Рисунок 33
Рисунок 34
Рисунок 35
Рисунок 36
Рисунок 37
|
||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 2563; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.011 с.) |

 (рисунок 32).
(рисунок 32).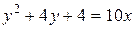 (рисунок 33).
(рисунок 33). ,
,  (рисунок 34).
(рисунок 34).