Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
А. Н. Благовисная, С. Т. ДусакаеваСодержание книги
Поиск на нашем сайте МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение высшего профессионального образования
«Оренбургский государственный университет»
Кафедра прикладной математики
А.Н. БЛАГОВИСНАЯ, С.Т. ДУСАКАЕВА
ПРИМЕНЕНИЕ МATHCAD ПРИ РЕШЕНИИ ЗАДАЧ ЛИНЕЙНОЙ АЛГЕБРЫ И АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Рекомендовано к изданию Редакционно-издательским советом государственного образовательного учреждения высшего профессионального образования «Оренбургский государственный университет»
Оренбург 2005 ББК
УДК
Рецензенты кандидат физико-математических наук, доцент Т.П. Петухова кандидат физико-математических наук, доцент Т.М. Отрыванкина
А.Н. Благовисная, С.Т. Дусакаева Применение Mathcad при решении задач линейной алгебры и аналитической геометрии: Методические указания. – Оренбург: ГОУ ОГУ, 2005. – 56с.
Методические указания предназначены для студентов специальности 010501 – Прикладная математика и информатика.
© А.Н. Благовисная, 2005 © С.Т. Дусакаева, 2005 © ГОУ ОГУ, 2005
Содержание
Введение
Предметы «Геометрия» и «Алгебра» нуждаются в применении информационных технологий, так как решение большинства задач в алгебре предполагает выполнение колоссального объема рутинной работы, что иногда затрудняет восприятие основных идей данного предмета, а в аналитической геометрии точное и наглядное выполнение рисунков существенно облегчает решение задачи. Для внедрения информационных технологий в образовательный процесс был выбран пакет Mathcad, который обладает дружественным по отношению к пользователю интерфейсом, а также математически и визуально ориентированным языком общения с пользователем, что поможет студентам первого курса достаточно легко овладеть основными навыками работы с данным пакетом. В методических указаниях приведены четыре лабораторных работы по дисциплине. В каждой лабораторной работе создана специальная система заданий, позволяющая закрепить и обобщить знания, полученные при изучении в линейной алгебры и аналитической геометрии. Методические указания содержат приложения, в которых наглядно показаны решения простейших задач в Mathcad на рисунках, отображающих диалоговое окно системы, что позволит студентам быстрее сориентироваться при выполнении задач для самостоятельного решения. Методические указания предназначены для студентов специальности 010501 – Прикладная математика и информатика и могут быть использованы при обучении студентов физико-математических, инженерных и экономических специальностей.
Лабораторная работа № 1
Тема: Выполнение матричных операций в среде Mathcad. Цель: Рассмотреть возможности применения пакета Mathcad при решении теоретических и практических задач линейной алгебры, в которых используются матричные операции. Порядок выполнения работы: 1) Повторить некоторые теоретические сведения, известные из курса линейной алгебры и необходимые для выполнения работы. 2) Рассмотреть примеры выполнения операций над матрицами в пакете Mathcad в Приложении А. 3) Выполнить задачи для самостоятельного решения по вариантам. Вариант соответствует порядковому номеру в журнале. 4) Написать отчет (в свободной форме).
Лабораторная работа № 2 Основные теоретические сведения, необходимые для выполнения лабораторной работы. Метод Крамера Пусть дана невырожденная система
тогда данная система совместна и единственное решение, которое может быть найдено по формулам Крамера
где
Метод Гаусса
Алгоритм этого метода состоит в следующем. Предположим, что коэффициент
Этого всегда можно добиться, переставляя в случае необходимости уравнения из системы или неизвестной в ней и меняя нумерацию неизвестных. Умножим первое уравнение на
В системе (2.2) следует вычеркнуть уравнения вида Следующие шаги прямого хода метода Гаусса осуществляются аналогично. Так, на втором шаге при Возможно, что на некотором шаге прямого хода метода Гаусса встретится уравнение вида
Тогда рассматриваемая система несовместна, и дальнейшие ее решение прекращается. Если же при выполнении прямого хода метода Гаусса не встретятся уравнения вида (2.3), то рассматриваемая система не более чем через
Для упрощения записи в системе (2.4) штрихи над коэффициентами опущены. В ней не более При
и в ней легко совершить обратный ход метода Гаусса. Для этого из последнего уравнения этой системы найдем значение неизвестного При
которые составляют общее решение системы (2.1). Из общего решения (2.6) при конкретных значениях На практике метод Гаусса обычно реализуют в матричной форме. Для этого выписывают расширенную матрицу системы, в которой для удобство отделяют вертикальной чертой столбец свободных членов, и преобразования проводят над этой матрицей, затем над полученной и т.д.
Матричный метод
Решение системы
Рассмотрим матрицы
Вопрос о совместности системы линейных уравнений (2.2) полностью решается следующей теоремой. Теорема Кронекера-Капелли: Система линейных уравнений (2.2) тогда и только тогда совместна, когда ранг основной матрицы равен рангу расширенной системы. Правило решения произвольной системы линейных уравнений. Пусть дана совместная система линейных уравнений (2.2) и пусть основная матрица А этой системы имеет ранг r. Выбираем в А r линейно независимых строк и оставляем в системе (2.2) лишь уравнения, коэффициенты которых вошли в выбранные строки. В этих уравнениях оставляем в левых частях такие r неизвестных, что определитель из коэффициентов при них отличен от нуля, а остальные неизвестные объявляем свободными и переносим в правые части уравнений. Давая свободным неизвестным произвольные числовые значения и вычисляя значения остальных неизвестных любым из методов, приведенных в пункте 1, мы получим все решения системы (2.2). Задания для самостоятельного выполнения.
В заданиях данной лабораторной работы N – номер варианта.
1. Доказать, что система имеет единственное решение и найти его матричным методом:
2. Исследовать систему на совместность. Если система совместна, то определить, сколько решений она имеет и, в зависимости от этого, найти решение системы или построить общее решение, используя метод Крамера. Сделать проверку.
а) б)
3. Исследовать систему на совместность. Если система совместна, то определить, сколько решений она имеет и, в зависимости от этого, найти решение системы методом Гаусса или построить общее решение, используя символьные вычисления системы Mathcad. Сделать проверку.
а)
б) в)
Лабораторная работа № 3
Эллипс Эллипсом называется геометрическое место точек, сумма расстояний которых до двух данных точек, называемых фокусами, есть постоянная величина 2 а, большая, чем расстояние между фокусами 2 с. Гипербола Гиперболой называется геометрическое место точек, разность расстояний от которых до двух данных точек (фокусов) есть постоянная величина 2 а, причем 2 a <2 c, где 2 с – расстояние между фокусами. Каноническое уравнение гиперболы, симметричной относительно осей координат, имеет вид
где Параметр а называется вещественной полуосью гиперболы и представляет собой расстояние от начала координат до вершины гиперболы, параметр b называется мнимой полуосью. Эксцентриситетом гиперболы называется величина Расстояния текущей М (х,y) гиперболы до фокусов (фокальные радиусы) определяются по формулам
Прямые, заданные уравнениями
Парабола Параболой называется геометрическое место точек, одинаково удаленных от данной точки (фокуса) и данной прямой (директрисы). Каноническое уравнение параболы, проходящей через начало координат и симметричной оси Ох, имеет вид
Уравнение вида
описывает параболу, симметричную относительно оси Оу. Фокальный радиус точки М (х,y), т.е. ее расстояние до фокуса на оси Ох, находится по формуле
Парабола, ось которой параллельна оси Оу, описывается уравнением Задания для самостоятельного выполнения:
Построить кривые II порядка и определить их тип. Для эллипса найти координаты фокусов, эксцентриситет и фокальные радиусы. Для гиперболы найти координаты фокусов, эксцентриситет, фокальные радиусы и уравнения асимптоты. Для параболы найти координаты фокуса и фокальный радиус. 1 вариант а) г) ж) у 2 + 4 х = 0 з) х 2 – 4 = 0 и) у 2 + 4 = 0
к) 2 вариант а)
г)
ж) х 2 – 4 у = 0 з) у 2 – 18 = 0 и) х 2 + 10 = 0
к) 3 вариант а)
г) 5 х 2 + 10 у 2 = 0 д) х 2 – у 2 = 0 е) 10 у 2 = 0
ж) у 2 – 10 х =0 з) у 2 –16 = 0 и) у2 + 16 = 0
к) 4 вариант а) 15 х 2 +100 у 2 = 12 б)
г)
ж) к) 5 вариант а) 20 х 2 +120 у 2 = 10 б)
г)
ж) к) 6 вариант а) 15 х 2 + у 2 = 60 б)
г)
ж) к) 7 вариант а) 20 х 2 + 40 у 2 = 100 б)
г)
ж) к) 8 вариант а) 15 х 2 + 5 у 2 = 60 б)
г)
ж)
к) 9 вариант а) х 2 + 20 у 2 = 100 б)
г)
ж)
к)
10 вариант а) 5 у 2 + 20 х 2 = 60 б)
г)
ж) к) 11 вариант а) 5 х 2 + 6 у 2 = 120 б)
г)
ж) к) 12 вариант а) 15 х 2 + 16 у 2 = 80 б)
г)
ж) к) 13 вариант а) 8 х 2 + 16 у 2 = 20 б)
г)
ж) к) 14 вариант а) 18 х 2 +40 у 2 =36 б)
г)
ж) к) 15 вариант а) 15 х 2 + 45 у 2 = 100 б)
г)
ж) к) 16 вариант а) 5 х 2 + 40 у 2 = 50 б)
г)
ж) к)
Лабораторная работа № 4
Приложение А
Выполнение матричных операций (сложение матриц, умножение матрицы на действительное число, умножение матриц, транспонирование матрицы, нахождение определителя квадратной матрицы, нахождение обратной матрицы, нахождение ранга матрицы) в среде Mathcad
Работа с матрицами в Mathcad. Большинство операций с матрицами в Mathcad можно выполнить тремя способами – с помощью панелей инструментов, выбором операций в меню или обращением к соответствующей функции. Панель операций с матрицами и векторами Matrix находится в панели математических инструментов (рисунок 1):
Рисунок 1 Открыть эту панель можно щелчком по соответствующей кнопке
Рисунок 2
Для того чтобы выполнить какую-либо операцию с помощью панели инструментов, нужно выделить матрицу и щелкнуть по кнопке операции либо щелкнуть по кнопке в панели и ввести в помеченной позиции имя матрицы. Меню символьных операций с матрицами (рисунок 2) содержит три функции – транспонирование, обращение матрицы и вычисление определителя матрицы. Чтобы произвести эти операции через меню нужно выделить матрицу и щелкнуть в меню по строке операции. Функции, предназначенные для работы с матрицами, находятся в разделе Vector and Matrix в пункте «Функция» в меню «Вставка» (рисунок 3).
Рисунок 3
Рассмотрим ряд необходимых нам функций. Функции определения матриц и операции с блоками матриц: matri x (m, n, f) – создает и заполняет матрицу размерности mxn, элемент которой, расположенный в i -той строке, j -том столбце, равен значению f (i, j) функции f (x,y); diag(v) – создает диагональную матрицу, элементы главной диагонали которой хранятся в векторе v; identity(n) – создает единичную матрицу порядка n; augment(A,B) – формирует матрицу, в первых столбцах которой содержится матрица A, а в последних – матрица B (матрицы A и B должны иметь одинаковое число строк); stak(A,B) – формирует матрицу, в первых строках которой содержится матрица A, а в последних – матрица B (матрицы A и B должны иметь одинаковое число столбцов). Функции вычисления числовых характеристик матриц: rows(A) – вычисление числа строк в матрице A; cols(A) – вычисление числа столбцов в матрице A; max(A) – вычисление наибольшего элемента в матрице A; min(A) – вычисление наименьшего элемента в матрице A; rank(A) – вычисление ранга матрицы A. Функции, реализующие численные алгоритмы решения задач линейной алгебры: rref(A) – приведение матрицы к ступенчатому виду с единичным базисным минором (выполняет элементарные операции со строками матрицы). lsolve(A,B) – решение системы линейных уравнений AX = B.
Задание 1. Задайте матрицу А размером 5х7 с использованием панели операций с матрицами и векторами Matrix и матрицу В того же размера с помощью функции определения матриц. Найдите 12 А -16 В (рисунок 4).
Рисунок 4
Задание 2. Задайте матрицу С размера 4х3 любым из описанных выше способов. Найдите транспонированную ей матрицу с помощью панели операций с матрицами и векторами Matrix, а также с использованием меню символьных операций с матрицами. Решение задания приведено на рисунке 5. Задание 3. Задайте матрицы P размера 6х8 и H размера 8х2. Найдите произведение матриц РН. Решение данного задания приведено на рисунке 6. Задание 4. Задайте квадратную матрицу D четвертого порядка и матрицу-столбец F с четырьмя строками любым из описанных выше способов, а также единичную матрицу соответствующей размерности с использованием функции определения матриц. Найдите произведения DF, DЕ и ЕD (рисунок 7). Задание 5. Задайте квадратную матрицу G четвертого порядка. Найдите обратную матрицу для матрицы G. Сделайте проверку (рисунок 8).
Рисунок 5
Рисунок 6
Рисунок 7
Рисунок 8
Задание 6. Найти 15 AB -29 CE + D 3-18 FGт +38 H -1, где Задание 7. Найдите определитель матрицы А четвертого порядка несколькими способами. Решение задания показано на рисунке 10. Задание 8. Найдите ранг матрицы размера 12х7. Решение задания на рисунке 11.
Рисунок 9
Рисунок 10
Рисунок 11.
Приложение Б Метод Крамера.
Задание 1. Решить систему линейных алгебраических уравнений методом Крамера
Возможности Mathcad позволяют использовать метод Крамера не только при нахождении решения невырожденной системы, но и для нахождения общего решения системы, имеющей бесконечно много решений. Для этого используется нахождение определителя как функции, зависящей от свободных переменных.
Задание 2. Решить систему
Метод Гаусса в системе Mathcad можно осуществить с помощью функции rref. Задание 3. Найдите решение системы линейных уравнений
Рисунок 12
Рисунок 13
Рисунок 14
Задание 4. Исследовать систему Возможен еще один способ решения системы линейных уравнений в Mathcad с помощью функции lsolve. Задание 5. Решить систему линейных уравнений
Рисунок 15
Рисунок 16
Приложение В Рисунок 20
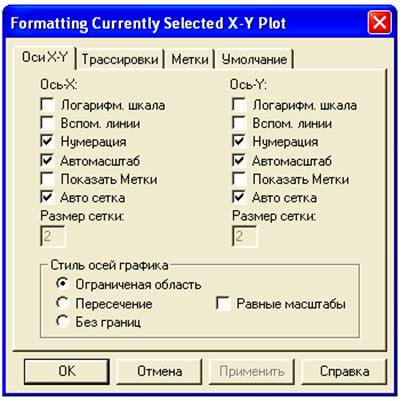
Диалоговое окно форматирования имеет четыре вкладки: Оси X-Y – задание параметров отображения осей; Трассировки (Линии) – задание параметров отображения линий графика; Метки – задание параметров отображения меток (надписей) у осей; Умолчание – задание параметров по умолчанию. Все параметры форматирования относятся к выделенному графику и могут при необходимости меняться.
Рисунок 21 Задание1. Построить график функции Задание 2. Построить в одной системе координат графики трех функций. Решение задания на рисунке 24. Задание 3. Построить кривую Задание 4. Построить кривые В пакете Mathcad также возможно построение кривых, заданных в полярных координатах и в параметрической форме. Примеры таких построений приведены на рисунках 28 и 29.
Рисунок 23
Рисунок 24
Рисунок 25
Рисунок 26
Рисунок 27
Рисунок 28
Рисунок 29
Приложение Г Рисунок 30
Рисунок 31
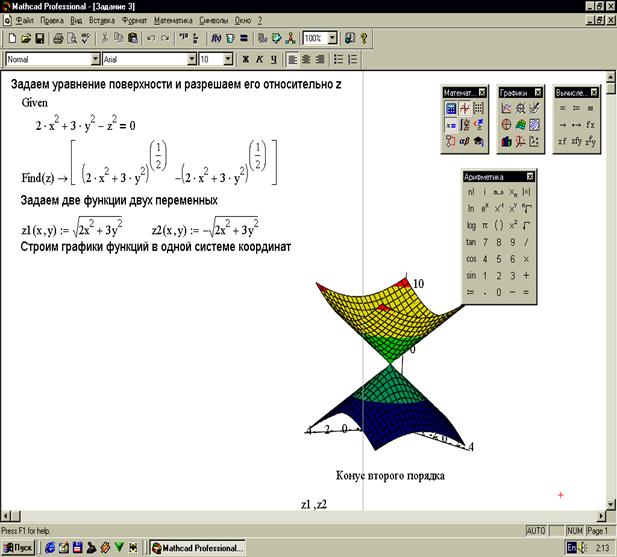
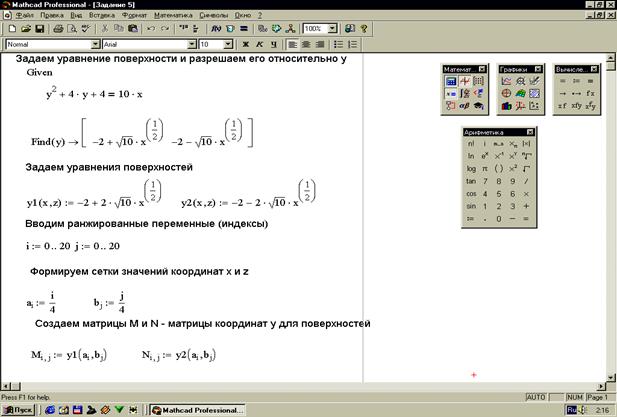
Уравнение поверхности не всегда задается в явном виде. Для того чтобы построить поверхность заданную неявно необходимо сначала уравнение данной поверхности разрешить относительно какой-либо переменной, а затем строить поверхности по полученным уравнениям. Задание 3. Построить поверхность, заданную уравнением Задание 4. Построить поверхность, заданную уравнением Возможности системы Mathcad позволяют строить пересекающиеся поверхности в одной системе координат. Задание 5. Построить поверхности В пакете Mathcad также возможно построение поверхностей, заданных в параметрической форме. Примеры таких построений приведены на рисунках 36 и 37.
Рисунок 32
Рисунок 33
Рисунок 34
Рисунок 35
Рисунок 36
Рисунок 37
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение высшего профессионального образования
«Оренбургский государственный университет»
Кафедра прикладной математики
А.Н. БЛАГОВИСНАЯ, С.Т. ДУСАКАЕВА
ПРИМЕНЕНИЕ МATHCAD ПРИ
|
||||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 461; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.014 с.) |

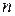 линейных уравнений с
линейных уравнений с  (2.1)
(2.1)
 - определитель основной матрицы системы,
- определитель основной матрицы системы,  - вспомогательные определители, получаемые из
- вспомогательные определители, получаемые из 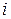 - ого столбца столбцов сводных членов.
- ого столбца столбцов сводных членов.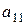 системы (2.1) отличен от нуля.
системы (2.1) отличен от нуля. (2.1)
(2.1) и вычтем из второго уравнения, затем на
и вычтем из второго уравнения, затем на  и вычтем из третьего уравнения и т.д. Наконец, умножим первое уравнение на
и вычтем из третьего уравнения и т.д. Наконец, умножим первое уравнение на  и вычтем из последнего уравнения. В результате неизвестной
и вычтем из последнего уравнения. В результате неизвестной  будет исключена из всех уравнений, кроме первого, и система примет вид:
будет исключена из всех уравнений, кроме первого, и система примет вид: (2.2)
(2.2) , если такие появились. На этом первый шаг метода Гаусса заканчивается. Элемент
, если такие появились. На этом первый шаг метода Гаусса заканчивается. Элемент  последовательно умножаем второе уравнение на
последовательно умножаем второе уравнение на  , ….,
, ….,  и вычитаем его из 3-го, 4-го, …,
и вычитаем его из 3-го, 4-го, …, 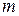 - го уравнений. В результате неизвестной
- го уравнений. В результате неизвестной  исключается из всех уравнений, кроме 1-го, 2-го. На третьем шаге неизвестное
исключается из всех уравнений, кроме 1-го, 2-го. На третьем шаге неизвестное  исключается из всех уравнений, кроме первых трех, и т.д.
исключается из всех уравнений, кроме первых трех, и т.д. (2.3)
(2.3) (2.4)
(2.4) , т.к. некоторые уравнения, возможны, были приведены к виду 0=0 и вычеркнуты.
, т.к. некоторые уравнения, возможны, были приведены к виду 0=0 и вычеркнуты.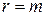 система (2.4) имеет треугольный вид:
система (2.4) имеет треугольный вид: (2.5)
(2.5) . Подставим его в предпоследнее уравнение, найдем значение
. Подставим его в предпоследнее уравнение, найдем значение  . Продолжая так далее, однозначно определим все неизвестные
. Продолжая так далее, однозначно определим все неизвестные  . Следовательно, если система (2.1) при прямом ходе метода Гаусса сводится к системе треугольного вида, то такая система определенная, т.е. имеет единственное решение.
. Следовательно, если система (2.1) при прямом ходе метода Гаусса сводится к системе треугольного вида, то такая система определенная, т.е. имеет единственное решение. система (2.4) имеет вид трапеции. В ней неизвестные
система (2.4) имеет вид трапеции. В ней неизвестные  принимают за базисные, а неизвестные
принимают за базисные, а неизвестные 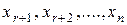 - за свободные. Свободные неизвестные могут принимать любые фиксированные значения. Полагая
- за свободные. Свободные неизвестные могут принимать любые фиксированные значения. Полагая  где
где  - произвольные постоянные, и проведя в системе обратный ход метода Гаусса получим формулы:
- произвольные постоянные, и проведя в системе обратный ход метода Гаусса получим формулы: (2.6)
(2.6)
 будут получатся частные решения системы (2.1). Так как каждое свободное неизвестное может принимать бесчисленное множество значений, система (2.1) при
будут получатся частные решения системы (2.1). Так как каждое свободное неизвестное может принимать бесчисленное множество значений, система (2.1) при  , т.е. в случае когда она приводится к трапецеидальному виду, обладает бесчисленным множеством решений. Это справедливо для совместных систем, имеющих меньше уравнений чем неизвестных, и, в частности, для однородных, имеющих меньше уравнений, чем неизвестных.
, т.е. в случае когда она приводится к трапецеидальному виду, обладает бесчисленным множеством решений. Это справедливо для совместных систем, имеющих меньше уравнений чем неизвестных, и, в частности, для однородных, имеющих меньше уравнений, чем неизвестных. в матричной форме имеет вид:
в матричной форме имеет вид: где
где 
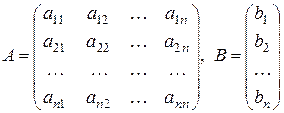
 - основная матрица системы (2.2)
- основная матрица системы (2.2) - расширенная матрица системы (2.2)
- расширенная матрица системы (2.2)
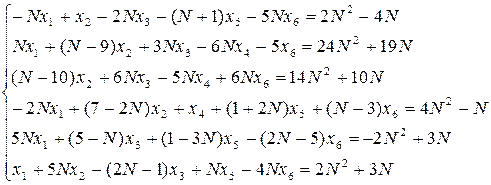

 ,
, ,
, .
.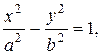
 .
. .
. .
. , являются асимптотами гиперболы.
, являются асимптотами гиперболы.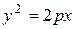 .
.
 .
. .
. б)
б) 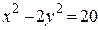 в)
в) 
 д)
д)  е) 5 у 2=0
е) 5 у 2=0
 б)
б)  в)
в) 
 д) 20 х 2 = 5 у 2 е) 150 х 2 = 0
д) 20 х 2 = 5 у 2 е) 150 х 2 = 0
 б)
б)  в) х 2 + у 2 + 1= 0
в) х 2 + у 2 + 1= 0
 в)
в) 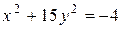
 д)
д) 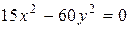 е) 20 х 2 = 0
е) 20 х 2 = 0 з) у 2 + 4 = 0 и) у 2 – 16 = 0
з) у 2 + 4 = 0 и) у 2 – 16 = 0
 в)
в) 
 д)
д)  е) 15 х 2 = 0
е) 15 х 2 = 0 з) 2 х 2 + 4 = 0 и) х 2 – 8 = 0
з) 2 х 2 + 4 = 0 и) х 2 – 8 = 0
 в)
в) 
 д)
д)  е) 100 х 2 = 0
е) 100 х 2 = 0 з) 12 у 2 + 8 = 0 и) у 2 – 12 = 0
з) 12 у 2 + 8 = 0 и) у 2 – 12 = 0
 в)
в) 
 д)
д) 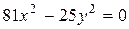 е) 64 х 2 = 0
е) 64 х 2 = 0 з) 5 у 2 + 10 = 0 и) 2 у 2 – 5 = 0
з) 5 у 2 + 10 = 0 и) 2 у 2 – 5 = 0
 в)
в) 
 д)
д)  е) 115 х 2 = 0
е) 115 х 2 = 0 з) х 2 + 3 = 0 и) 5 х 2 = 10
з) х 2 + 3 = 0 и) 5 х 2 = 10
 в)
в) 
 д)
д)  е) 22 у 2 = 0
е) 22 у 2 = 0 з) 5 у 2 +7 = 0 и) 5 у 2 =12
з) 5 у 2 +7 = 0 и) 5 у 2 =12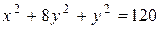
 в)
в) 
 д)
д)  е) 156 у 2 = 0
е) 156 у 2 = 0
 в)
в) 
 д)
д)  е) 1112 х 2 = 0
е) 1112 х 2 = 0
 в)
в) 
 д)
д)  е) 21 у 2 = 0
е) 21 у 2 = 0 з) 12 х 2 + 8 = 0 и) 5 х 2 = 10
з) 12 х 2 + 8 = 0 и) 5 х 2 = 10
 в)
в) 
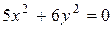 д)
д)  е) 51 х 2 = 0
е) 51 х 2 = 0 з) 5 у 2 + 6 = 0 и) 2 у 2 = 6
з) 5 у 2 + 6 = 0 и) 2 у 2 = 6
 в)
в) 
 д)
д)  з) 12 х 2 + 8 = 0 и) 3 х 2 = 8
з) 12 х 2 + 8 = 0 и) 3 х 2 = 8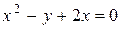
 в)
в) 
 д)
д)  е) 22 у 2 = 0
е) 22 у 2 = 0 з) 16 х 2 + 144 = 0 и) у 2 = 12
з) 16 х 2 + 144 = 0 и) у 2 = 12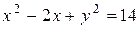
 в)
в) 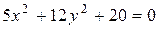
 е) 11 х 2 = 0
е) 11 х 2 = 0 з) 15 х 2 + 12 = 0 и) 16 у 2 = 8
з) 15 х 2 + 12 = 0 и) 16 у 2 = 8 .
.
 . За каждой кнопкой панели закреплены функции. Рассмотрим лишь необходимые нам кнопки и их функции:
. За каждой кнопкой панели закреплены функции. Рассмотрим лишь необходимые нам кнопки и их функции: определение размеров матрицы;
определение размеров матрицы; ввод нижнего индекса;
ввод нижнего индекса; нахождение обратной матрицы;
нахождение обратной матрицы; вычисление определителя матрицы;
вычисление определителя матрицы; выделение n-го столбца матрицы М (нумерация начинается с нуля).
выделение n-го столбца матрицы М (нумерация начинается с нуля).






 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  , E – единичная матрица соответствующей размерности. Решение задания на рисунке 9.
, E – единичная матрица соответствующей размерности. Решение задания на рисунке 9.


 . Решение задания на рисунке 12.
. Решение задания на рисунке 12. методом Крамера. Решение задания на рисунке 13.
методом Крамера. Решение задания на рисунке 13. с помощью функции rref. Решение задания на рисунке 14.
с помощью функции rref. Решение задания на рисунке 14.


 на совместность. Если система совместна, то найти ее общее решение. Решение задания на рисунке 15.
на совместность. Если система совместна, то найти ее общее решение. Решение задания на рисунке 15. с применением функции lsolve. Решение задания на рисунке 16.
с применением функции lsolve. Решение задания на рисунке 16.

 , выбрав шаблон любым из описанных способов. Задайте более подходящий масштаб. Измените стиль осей графика. Измените цвет линий графика. Задайте надписи у осей. Решение задания на рисунке 23.
, выбрав шаблон любым из описанных способов. Задайте более подходящий масштаб. Измените стиль осей графика. Измените цвет линий графика. Задайте надписи у осей. Решение задания на рисунке 23.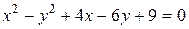 . Определить тип кривой. Решение задания на рисунке 25.
. Определить тип кривой. Решение задания на рисунке 25. и
и  , найти их точки пересечения. Решение задания на рисунках 26 и 27.
, найти их точки пересечения. Решение задания на рисунках 26 и 27.






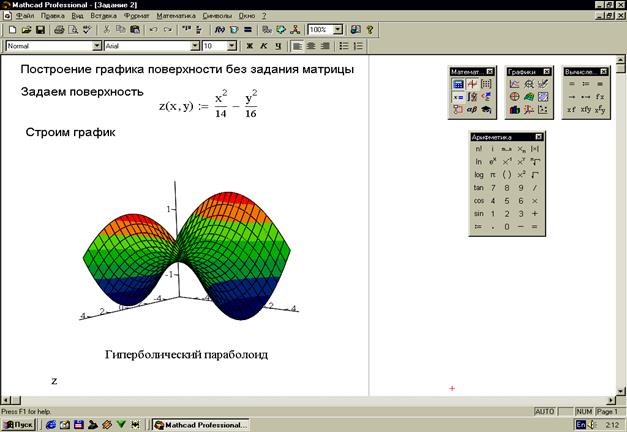
 (рисунок 32).
(рисунок 32).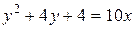 (рисунок 33).
(рисунок 33). ,
,  (рисунок 34).
(рисунок 34).