
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Найти точки пересечения кривых второго порядкаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1) 3) 5) 7) 9) 11) 13) 15)
3 Определить вид кривой, заданной уравнением а) б) в) г) д) е) ж)
Лабораторная работа № 4
Тема: Построение поверхностей второго порядка. Цель: Рассмотреть возможности построения поверхностей второго порядка в системе Mathcad Порядок выполнения работы: 1) Повторить некоторые теоретические сведения, известные из курса аналитической геометрии, необходимые для выполнения работы. 2) Рассмотреть примеры построения поверхностей второго порядка в Mathcad в Приложении Г. 3) Выполнить задачи для самостоятельного решения по вариантам. Вариант соответствует порядковому номеру в журнале. 4) Написать отчет (в свободной форме).
Основные теоретические сведения, необходимые для выполнения лабораторной работы.
Общее уравнение поверхности второго порядка. относительно некоторой прямоугольной системы координат имеет вид:
где
Существует 17 поверхностей второго порядка в пространстве, описываемых в таблице 2
Таблица 2.
Задания для самостоятельного выполнения:
Построить следующие поверхности второго порядка 1) 3) 5) 7) 9) 11) 13) 15)
2 Построить поверхности второго порядка и определить их тип:
1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16)
Построить линию пересечения поверхности с плоскостью 1) 2) 3) 4) 5) 6) 7)
8) 9) 10) 11) 12) 13) 14)
15) 16)
Найти линию пересечения поверхностей второго порядка
1) 3) 5) 7) 9) 11) 13) 15) Приложение А
Выполнение матричных операций (сложение матриц, умножение матрицы на действительное число, умножение матриц, транспонирование матрицы, нахождение определителя квадратной матрицы, нахождение обратной матрицы, нахождение ранга матрицы) в среде Mathcad
Работа с матрицами в Mathcad. Большинство операций с матрицами в Mathcad можно выполнить тремя способами – с помощью панелей инструментов, выбором операций в меню или обращением к соответствующей функции. Панель операций с матрицами и векторами Matrix находится в панели математических инструментов (рисунок 1):
Рисунок 1 Открыть эту панель можно щелчком по соответствующей кнопке
Рисунок 2
Для того чтобы выполнить какую-либо операцию с помощью панели инструментов, нужно выделить матрицу и щелкнуть по кнопке операции либо щелкнуть по кнопке в панели и ввести в помеченной позиции имя матрицы. Меню символьных операций с матрицами (рисунок 2) содержит три функции – транспонирование, обращение матрицы и вычисление определителя матрицы. Чтобы произвести эти операции через меню нужно выделить матрицу и щелкнуть в меню по строке операции. Функции, предназначенные для работы с матрицами, находятся в разделе Vector and Matrix в пункте «Функция» в меню «Вставка» (рисунок 3).
Рисунок 3
Рассмотрим ряд необходимых нам функций. Функции определения матриц и операции с блоками матриц: matri x (m, n, f) – создает и заполняет матрицу размерности mxn, элемент которой, расположенный в i -той строке, j -том столбце, равен значению f (i, j) функции f (x,y); diag(v) – создает диагональную матрицу, элементы главной диагонали которой хранятся в векторе v; identity(n) – создает единичную матрицу порядка n;
augment(A,B) – формирует матрицу, в первых столбцах которой содержится матрица A, а в последних – матрица B (матрицы A и B должны иметь одинаковое число строк); stak(A,B) – формирует матрицу, в первых строках которой содержится матрица A, а в последних – матрица B (матрицы A и B должны иметь одинаковое число столбцов). Функции вычисления числовых характеристик матриц: rows(A) – вычисление числа строк в матрице A; cols(A) – вычисление числа столбцов в матрице A; max(A) – вычисление наибольшего элемента в матрице A; min(A) – вычисление наименьшего элемента в матрице A; rank(A) – вычисление ранга матрицы A. Функции, реализующие численные алгоритмы решения задач линейной алгебры: rref(A) – приведение матрицы к ступенчатому виду с единичным базисным минором (выполняет элементарные операции со строками матрицы). lsolve(A,B) – решение системы линейных уравнений AX = B.
Задание 1. Задайте матрицу А размером 5х7 с использованием панели операций с матрицами и векторами Matrix и матрицу В того же размера с помощью функции определения матриц. Найдите 12 А -16 В (рисунок 4).
Рисунок 4
Задание 2. Задайте матрицу С размера 4х3 любым из описанных выше способов. Найдите транспонированную ей матрицу с помощью панели операций с матрицами и векторами Matrix, а также с использованием меню символьных операций с матрицами. Решение задания приведено на рисунке 5. Задание 3. Задайте матрицы P размера 6х8 и H размера 8х2. Найдите произведение матриц РН. Решение данного задания приведено на рисунке 6. Задание 4. Задайте квадратную матрицу D четвертого порядка и матрицу-столбец F с четырьмя строками любым из описанных выше способов, а также единичную матрицу соответствующей размерности с использованием функции определения матриц. Найдите произведения DF, DЕ и ЕD (рисунок 7). Задание 5. Задайте квадратную матрицу G четвертого порядка. Найдите обратную матрицу для матрицы G. Сделайте проверку (рисунок 8).
Рисунок 5
Рисунок 6
Рисунок 7
Рисунок 8
Задание 6. Найти 15 AB -29 CE + D 3-18 FGт +38 H -1, где Задание 7. Найдите определитель матрицы А четвертого порядка несколькими способами. Решение задания показано на рисунке 10. Задание 8. Найдите ранг матрицы размера 12х7. Решение задания на рисунке 11.
Рисунок 9
Рисунок 10
Рисунок 11.
Приложение Б
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 534; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.148.145.124 (0.011 с.) |

 ,
,  . 2)
. 2)  .
. 4)
4) 
 . 6)
. 6)  .
. . 8)
. 8)  .
. . 10)
. 10) 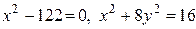 .
. . 12)
. 12)  .
. . 14)
. 14)  .
. . 16)
. 16)  .
. , построив её
, построив её ,
,
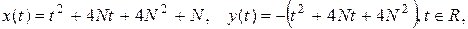





 (4.4)
(4.4) .
.





























 ; 2)
; 2) 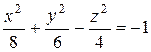 ;
; ; 4)
; 4)  ;
; ; 6)
; 6)  ;
; ; 8)
; 8)  ;
; ; 10)
; 10)  ;
; ; 12)
; 12)  ;
; ; 14)
; 14)  ;
; ; 16)
; 16)  .
. ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
;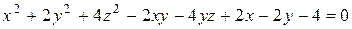 ;
; ;
; ;
; ;
; ;
; ;
; .
. и
и  ;
; ;
; и
и  ;
; и
и  ;
; ;
; и (хоу);
и (хоу); и (уоz);
и (уоz); и (zox);
и (zox);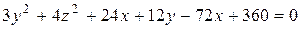 и x-y+z =1;
и x-y+z =1; и 2 х-у+z =0;
и 2 х-у+z =0; и
и  ;
; и
и  ;
; и x+y+ 7 z -13=0;
и x+y+ 7 z -13=0; и
и ;
; и
и  ;
; и
и  .
. ; 2)
; 2)  ;
; ; 4)
; 4)  ;
; ; 6)
; 6)  ;
; ; 8)
; 8)  ;
; ; 10)
; 10)  ;
; ; 12)
; 12)  ;
; ; 14)
; 14)  ;
; ; 16)
; 16)  .
.
 . За каждой кнопкой панели закреплены функции. Рассмотрим лишь необходимые нам кнопки и их функции:
. За каждой кнопкой панели закреплены функции. Рассмотрим лишь необходимые нам кнопки и их функции: определение размеров матрицы;
определение размеров матрицы; ввод нижнего индекса;
ввод нижнего индекса; нахождение обратной матрицы;
нахождение обратной матрицы; вычисление определителя матрицы;
вычисление определителя матрицы; выделение n-го столбца матрицы М (нумерация начинается с нуля).
выделение n-го столбца матрицы М (нумерация начинается с нуля).






 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  , E – единичная матрица соответствующей размерности. Решение задания на рисунке 9.
, E – единичная матрица соответствующей размерности. Решение задания на рисунке 9.





