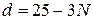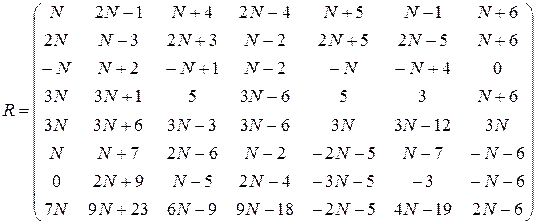Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные теоретические сведения, необходимые для выполнения лабораторной работы.Содержание книги
Поиск на нашем сайте
Определение 1. Матрицей называется совокупность
Кратко матрицу Определение 2. Определителем квадратной матрицы называется алгебраическая сумма всевозможных произведений элементов этой матрицы, взятых по одному из каждой строки и по одному из каждого столбца. Сомножители в каждом слагаемом записываются в порядке следования строк, тогда номера столбцов образуют перестановки; слагаемые, соответствующие четным перестановкам берутся со знаком «плюс», соответствующие нечетным – со знаком «минус». Определение 3. Квадратная матрица называется невырожденной, если ее определитель не равен нулю. Над матрицами определены пять действий: сложение, умножение на элементы основного поля (или кольца), умножение матрицы на матрицу, транспонирование, нахождение обратной. Определение 4. если для матрицы А существует матрица, обозначаемая Условия применимости и размеры результата поясняются следующими схемами:
Эти действия обладают свойствами: 1 2 3 4 5 6 7 8 Это – свойства векторного пространства, т.к. матрицы фиксированных размеров образуют векторное пространство. 9 10 11 12 13 14 15 16 17 18 19 20 21
Задания для самостоятельного выполнения:
В заданиях данной лабораторной работы N – номер варианта.
1. Проверить выполнение свойств 1-8 для матриц А, В, С и чисел
2. Среди указанных ниже матриц А, В, С, D, F и G найти те, которые удовлетворяют свойствам 9-13 и проверить выполнение этих свойств (
3. Проверить выполнение свойств 14-17 для матриц А и В. Будет ли выполняться равенство
Среди указанных ниже матриц найти перестановочные и проверить для них выполнение следующего равенства
где
5. Для каких матриц выполняются следующие утверждения: а) б)
6. Найти значение многочлена
7. Для данных квадратных матриц найти обратные матрицы, если такие существуют, и сделать проверку. Проверьте выполнимость свойств 18-21.
а) 8.Решить матричные уравнения и сделать проверку: а) б) 9. Найти
10. Вычислить определитель
где 11. Найти максимальное число линейно независимых столбцов матрицы R:
12. Найти линейно независимые строки матрицы T и показать, что данные строки линейно независимы:
Лабораторная работа № 2
|
|||||||||||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 318; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.132.23 (0.008 с.) |

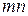 чисел, расположенных в виде прямоугольной таблицы
чисел, расположенных в виде прямоугольной таблицы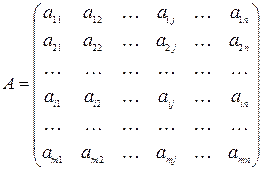 , содержащей
, содержащей 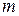 строк и
строк и 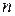 столбцов.
столбцов.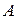 записывают в виде
записывают в виде 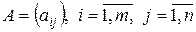 . Числа
. Числа 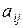 составляющие данную матрицу называют ее элементами. Если
составляющие данную матрицу называют ее элементами. Если  то матрица называется квадратной.
то матрица называется квадратной.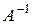 , обладающая свойством
, обладающая свойством  , то матрица
, то матрица 
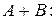

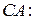

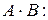

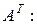
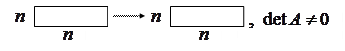
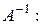
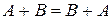
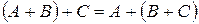
 O:
O: 
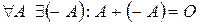
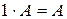


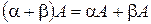
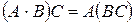

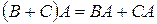
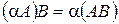
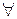
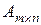
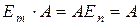
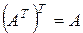



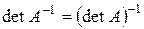
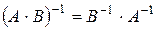

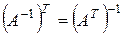
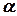 ,
, 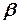 :
: ,
, ,
,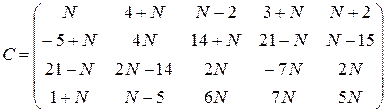 ,
,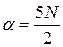 ,
, 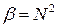 .
.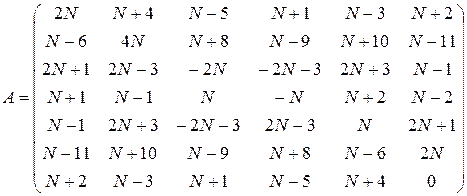 ,
,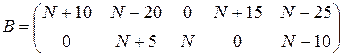 ,
,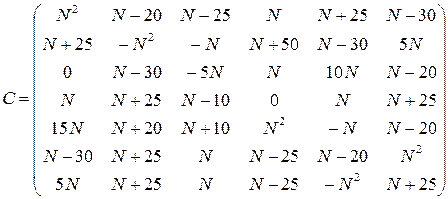 ,
, ,
, 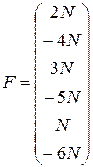 ,
,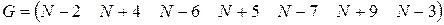 ,
,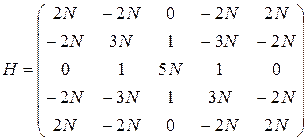 .
.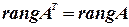 ?
?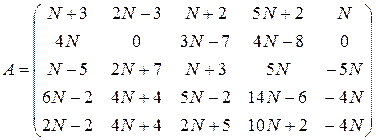 ,
,
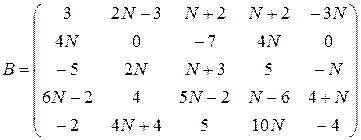 .
.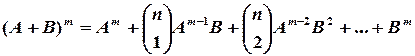 ,
,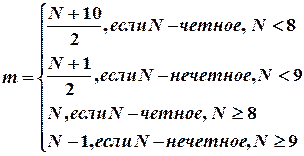
 ,
, 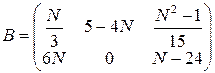 ,
,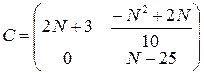 ,
, 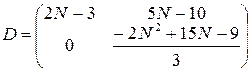 ,
,

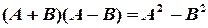 ?
?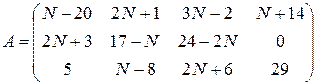 ,
, 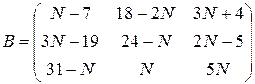 ,
,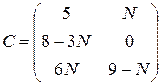 ,
, 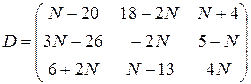
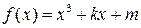 от матрицы Y, если
от матрицы Y, если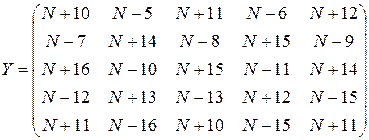 ,
, ,
, 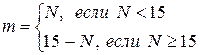
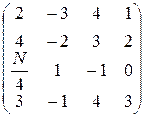 б)
б) 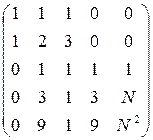
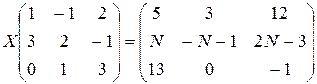
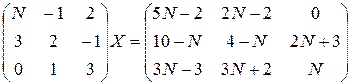
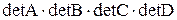 и
и 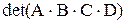 . Сделать вывод.
. Сделать вывод. ,
, 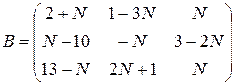 ,
,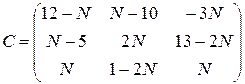 ,
, 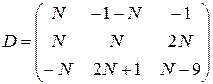
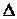 посредством умножения его на определитель
посредством умножения его на определитель 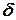 :
: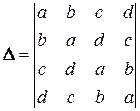 ,
, 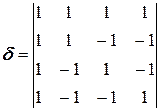 ,
,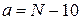 ,
, 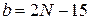 ,
, 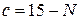 ,
,