
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общая теория линий второго порядкаСодержание книги
Поиск на нашем сайте
ОБЩАЯ ТЕОРИЯ ЛИНИЙ ВТОРОГО ПОРЯДКА Определение. Линией второго порядка называется множество всех точек плоскости, координаты которых в некоторой аффинной системе координат удовлетворяют алгебраическому уравнению второй степени
Пусть С каждым уравнением вида (1) связано число если если В свою очередь, каждый тип включает в себя несколько видов линий второго порядка (сопроводить примеры рисунками).
Линии эллиптического типа и их канонические уравнения: Эллипс: Мнимый эллипс: Пара мнимых прямых, пересекающихся в вещественной точке:
Линии гиперболического типа и их канонические уравнения: Гипербола с вещественной осью Ох: Пара пересекающихся прямых: Линии параболического типа и их канонические уравнения: Парабола с осью Ох: Пара параллельных прямых: Пара мнимых параллельных прямых: Пара совпавших прямых: РЕКОМЕНДАЦИИ: 1. Полезно заготовить таблицу на развороте тетради со следующими столбцами: 1) тип и Таблица заполняется по мере изучения материала рисунками и небольшими комментариями. 2) Хороший результат даёт следующий приём: задавать студентам на дом изготовление шпаргалок по каждой теме: название объекта (например, ЦЕНТР ЛИНИИ ВТОРОГО ПОРЯДКА), аналитическое задание изучаемого объекта, если надо – рисунок. Я разрешаю подсматривать в свои шпаргалки даже на контрольной работе. Но, как правило, к контрольной работе они уже не нужны…
ЦЕНТР ЛИНИИ ВТОРОГО ПОРЯДКА Определение. Точка С называется центром линии Теорема. Пусть
координаты удовлетворяют системе
где Если система (2) имеет единственное решение, то есть линия В остальных случаях (если система (2) не имеет решений (то есть линия Если каждое уравнение системы (2) рассматривать как уравнение прямой на плоскости, то становится очевидным (если забыли известные факты алгебры), что: система (2) имеет единственное решение система (2) не имеет решения система (2) имеет бесконечно много решений Для двух последних случаев Точка, принадлежащая линии Рассмотрите рисунки линий второго порядка и выясните, какие линии имеют особые точки.
ЗАДАЧИ. 1. Найдите центр для каждой из линий. Выясните вид каждой линии. а) Решение. Чтобы не делать «обидных» ошибок, подпишите под каждым коэффициентом в уравнении
Следите за знаками и не забывайте про «двойки». В данной задаче
Обязательно вычисляйте определитель
Решая систему, находим единственное решение С(3, -2). Чтобы определить вид линии, выясним, принадлежит ли центр С этой линии. Для этого подставим найденные координаты в уравнение линии Вычисляя, получаем, что координаты не удовлетворяют уравнению линии, то есть С не принадлежит ей. Значит, данная линия – гипербола.
б) Решение. Составим систему вида (2):
или
Очевидно, существует бесконечно много решений, все они описываются уравнением Выясним вид линии. Для этого найдём один из центров, например С(0,0), и выясним, принадлежит ли он линии В данном случае это несложно сделать подбором: А Подумайте, как быть, если не удаётся подобрать вещественную точку, принадлежащую линии.
2. а) б) в) Решение: а) б)
в)
3. Как выглядит общее уравнение линии второго порядка, если ось Ох является прямой её центров? Решение. Пусть Так как существует прямая центров, то Любая точка М(х, 0) является центром, поэтому
Точка О(0,0) – тоже центр, значит
Так как Окончательно получаем уравнение линии
4. Составьте уравнение линии второго порядка, проходящей через точки О(0, 0), А(0, 1), В(1, 0), если она симметрична относительно С(2, 3). Решение. Пусть О А В С – центр 2 Будем решать систему из пяти уравнений, в которой шесть неизвестных. Пусть Но тогда
СОПРЯЖЕННЫЕ ДИАМЕТРЫ.
Дана аффинная система координат Определение. Диаметром линии На лекции доказано, что диаметр – это прямая и получено её уравнение
или
Рекомендации: Показать (на эллипсе), как строится (задаём не асимптотическое направление; проводим [две] прямые этого направления, пересекающие линию; находим середины отсекаемых хорд; проводим через середины прямую – это и есть диаметр). Обсудить: 1. Почему в определении диаметра берётся вектор не асимптотического направления. Если не могут ответить, то попросите построить диаметр, например, для параболы. 2. Любая ли линия второго порядка имеет хотя бы один диаметр? Почему? 3. На лекции доказано, что диаметр – это прямая. Серединой какой хорды является точка М на рисунке?
М
4. Посмотрите на скобки в уравнении (7). Что они напоминают? Вывод: 1) каждый центр принадлежит каждому диаметру; 2) если существует прямая центров, то существует единственный диаметр. 5. Какое направление имеют диаметры линии параболического типа? (Асимптотическое) Доказательство (наверно, на лекции). Пусть диаметр d, заданный уравнением (7`) сопряжен вектору
6. Сколько диаметров у параболы? Их взаимное расположение? Сколько диаметров у остальных линий параболического типа? Почему? 7. Как построить общий диаметр некоторых пар линий второго порядка (см. вопросы 30, 31 далее). 8. Заполняем таблицу, обязательно делаем рисунки.
ЗАДАЧИ. 1. 2. Напишите уравнение диаметра d, проходящего через точку К(1,-2) для линии Этапы решения: 1-й способ. 1. Определяем тип (чтобы знать, как ведут себя диаметры этой линии). В данном случае линия центральная, тогда все диаметры проходят через центр С. 2. Составляем уравнение прямой, проходящей через две точки К и С. Это и есть искомый диаметр. 2-й способ. 1. Записываем уравнение диаметра d в виде (7`). 2. Подставив в это уравнение координаты точки К, находим зависимость между координатами вектора, сопряженного диаметру d. 3. Задаём этот вектор, учитывая найденную зависимость, и составляем уравнение диаметра d. В данной задаче вычислять проще вторым способом.
3.
4. Найдите середину хорды, отсекаемой линией
на прямой x + 3y – 12 =0. Указание к решению: Конечно, можно найти точки пересечения данных прямой и линии Возьмём направляющий вектор данной прямой и запишем уравнение диаметра, сопряжённого этому вектору. Далее, найдём точку пересечения данной прямой и найденного диаметра. СОПРЯЖЕННЫЕ НАПРАВЛЕНИЯ
Определение. Пусть Показать, как изобразить! Геометрический смысл: два диаметра сопряжены, если каждый из них делит пополам хорды, параллельные другому диаметру. Обсудить: У каждой ли линии второго порядка есть сопряжённые диаметры? Почему? Определение. Направления ненулевых векторов
На лекции доказывается, что сопряжённые диаметры имеют сопряжённые направления. ЗАДАЧИ. 5.(941) Напишите уравнения двух сопряжённых диаметров линии
6.(940) Напишите уравнения двух сопряжённых диаметров линии
Замечание. Прежде, чем приступать к вычислениям, сделайте иллюстрации к эти задачам! Обсудить: Какому направлению сопряжено асимптотическое направление относительно а) центральной линии Ответ: а) самому себе; б) любому направлению. (Возможно, это доказано на лекции. Если нет, можно рассмотреть в качестве задачи.)
Домашнее задание. [1] №№ 923, 924, 926, 938, 939, 945. Шпаргалки: 1) диаметры; 2) сопряженные диаметры.
ВОПРОСЫ ДЛЯ ПРОВЕДЕНИЯ ОТЧЁТА (ЗАЧЁТА) ОБЩАЯ ТЕОРИЯ ЛИНИЙ ВТОРОГО ПОРЯДКА Определение. Линией второго порядка называется множество всех точек плоскости, координаты которых в некоторой аффинной системе координат удовлетворяют алгебраическому уравнению второй степени
Пусть С каждым уравнением вида (1) связано число если если В свою очередь, каждый тип включает в себя несколько видов линий второго порядка (сопроводить примеры рисунками).
Линии эллиптического типа и их канонические уравнения: Эллипс: Мнимый эллипс: Пара мнимых прямых, пересекающихся в вещественной точке:
Линии гиперболического типа и их канонические уравнения: Гипербола с вещественной осью Ох: Пара пересекающихся прямых: Линии параболического типа и их канонические уравнения: Парабола с осью Ох: Пара параллельных прямых: Пара мнимых параллельных прямых: Пара совпавших прямых: РЕКОМЕНДАЦИИ: 1. Полезно заготовить таблицу на развороте тетради со следующими столбцами: 1) тип и Таблица заполняется по мере изучения материала рисунками и небольшими комментариями. 2) Хороший результат даёт следующий приём: задавать студентам на дом изготовление шпаргалок по каждой теме: название объекта (например, ЦЕНТР ЛИНИИ ВТОРОГО ПОРЯДКА), аналитическое задание изучаемого объекта, если надо – рисунок. Я разрешаю подсматривать в свои шпаргалки даже на контрольной работе. Но, как правило, к контрольной работе они уже не нужны…
ЦЕНТР ЛИНИИ ВТОРОГО ПОРЯДКА Определение. Точка С называется центром линии Теорема. Пусть координаты удовлетворяют системе
где Если система (2) имеет единственное решение, то есть линия В остальных случаях (если система (2) не имеет решений (то есть линия
Если каждое уравнение системы (2) рассматривать как уравнение прямой на плоскости, то становится очевидным (если забыли известные факты алгебры), что: система (2) имеет единственное решение система (2) не имеет решения система (2) имеет бесконечно много решений Для двух последних случаев Точка, принадлежащая линии Рассмотрите рисунки линий второго порядка и выясните, какие линии имеют особые точки.
ЗАДАЧИ. 1. Найдите центр для каждой из линий. Выясните вид каждой линии. а) Решение. Чтобы не делать «обидных» ошибок, подпишите под каждым коэффициентом в уравнении
Следите за знаками и не забывайте про «двойки». В данной задаче
Обязательно вычисляйте определитель
Решая систему, находим единственное решение С(3, -2). Чтобы определить вид линии, выясним, принадлежит ли центр С этой линии. Для этого подставим найденные координаты в уравнение линии Вычисляя, получаем, что координаты не удовлетворяют уравнению линии, то есть С не принадлежит ей. Значит, данная линия – гипербола.
б) Решение. Составим систему вида (2):
или Очевидно, существует бесконечно много решений, все они описываются уравнением Выясним вид линии. Для этого найдём один из центров, например С(0,0), и выясним, принадлежит ли он линии В данном случае это несложно сделать подбором: А Подумайте, как быть, если не удаётся подобрать вещественную точку, принадлежащую линии.
2. а) б) в) Решение: а) б)
в)
3. Как выглядит общее уравнение линии второго порядка, если ось Ох является прямой её центров? Решение. Пусть Так как существует прямая центров, то Любая точка М(х, 0) является центром, поэтому
Точка О(0,0) – тоже центр, значит
Так как Окончательно получаем уравнение линии
4. Составьте уравнение линии второго порядка, проходящей через точки О(0, 0), А(0, 1), В(1, 0), если она симметрична относительно С(2, 3). Решение. Пусть О А В С – центр 2 Будем решать систему из пяти уравнений, в которой шесть неизвестных. Пусть Но тогда
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 2585; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.241.93 (0.011 с.) |

 (1).
(1). - линия второго порядка, заданная уравнением (1).
- линия второго порядка, заданная уравнением (1). , которое называется определителем линии
, которое называется определителем линии 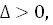
 - линия гиперболического типа,
- линия гиперболического типа,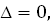


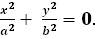
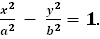
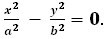
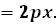
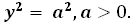

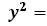 0.
0.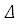 ; 2) каноническое уравнение; 3) название; 4) каноническая картинка в ПДСК; 5) центры; 6) асимптотические направления (асимптоты); 7) диаметры, сопряженные диаметры; 8) главные направления и главные диаметры (можно разбить на два столбца).
; 2) каноническое уравнение; 3) название; 4) каноническая картинка в ПДСК; 5) центры; 6) асимптотические направления (асимптоты); 7) диаметры, сопряженные диаметры; 8) главные направления и главные диаметры (можно разбить на два столбца).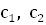 ) – центр линии
) – центр линии 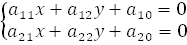 (2)
(2) 

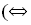 прямые пересекаются в одной точке)
прямые пересекаются в одной точке) 
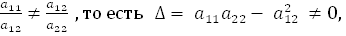 следовательно, центральными являются линии эллиптического и гиперболического типа;
следовательно, центральными являются линии эллиптического и гиперболического типа;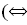 прямые параллельны)
прямые параллельны) 
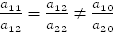 ;
; .
. второго порядка, называется особой точкой линии
второго порядка, называется особой точкой линии 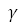 , если она является центром этой линии. В противном случае точка называется обыкновенной.
, если она является центром этой линии. В противном случае точка называется обыкновенной.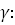 3
3 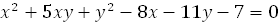
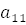 ,
, 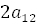 , и т.д.
, и т.д.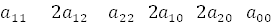
 =
=  ,
, 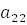 =1,
=1, 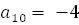 ,
,  ,
, 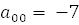 .
. так как выяснение типа влечёт за собой, как мы узнаем, много информации:
так как выяснение типа влечёт за собой, как мы узнаем, много информации:
 существует единственный центр. Найдём центр, для этого составим систему вида (2):
существует единственный центр. Найдём центр, для этого составим систему вида (2):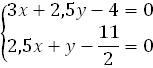

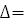 1
1 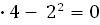
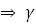 - параболического типа
- параболического типа 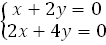
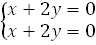 .
.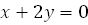 . Это означает, что существует прямая центров с уравнением
. Это означает, что существует прямая центров с уравнением 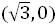 . Итак, окончательно получаем, что данная линия – пара вещественных параллельных прямых.
. Итак, окончательно получаем, что данная линия – пара вещественных параллельных прямых. . При каких
. При каких 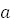 и
и 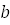 :
: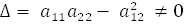
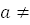 9.
9. 0 и
0 и 
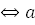 =9 и b
=9 и b  9.
9. .
.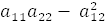 =0.
=0.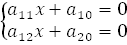 .
.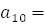
 . Но тогда
. Но тогда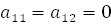 .
.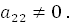
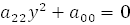 .
.
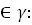
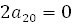

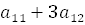 +
+ 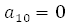
 + 3
+ 3 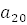
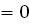 .
.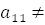 0. Удобно (в данном случае) считать
0. Удобно (в данном случае) считать 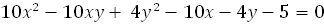 .
.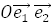 .
.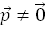 не асимптотического направления относительно
не асимптотического направления относительно 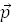 .
.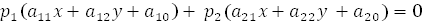 (7)
(7) (7`)
(7`)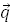 (-(
(-(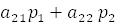 ),
), 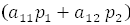 ). Покажем, что этот вектор имеет асимптотическое направление. Воспользуемся критерием вектора асимптотического направления для линии параболического типа (см.(5)). Подставляем и убеждаемся (не забываем, что
). Покажем, что этот вектор имеет асимптотическое направление. Воспользуемся критерием вектора асимптотического направления для линии параболического типа (см.(5)). Подставляем и убеждаемся (не забываем, что 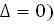 .
.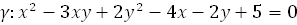 . Напишите уравнение множества середин всех хорд, параллельных вектору
. Напишите уравнение множества середин всех хорд, параллельных вектору 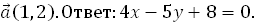
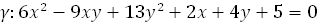 .
.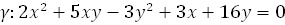 . Напишите уравнение диаметра, параллельного оси абсцисс.
. Напишите уравнение диаметра, параллельного оси абсцисс.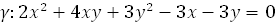
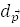 - диаметр, сопряжённый вектору
- диаметр, сопряжённый вектору 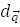 - диаметр, сопряжённый вектору
- диаметр, сопряжённый вектору 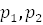 ) и
) и 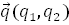 называются сопряжёнными направлениями относительно линии
называются сопряжёнными направлениями относительно линии 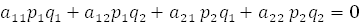 (8)
(8)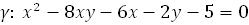 .
. если один из них проходит через точку М(-1,-2).
если один из них проходит через точку М(-1,-2). .
.


