
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Цепи с источниками гармонических воздействийСодержание книги
Поиск на нашем сайте ЦЕПИ С ИСТОЧНИКАМИ ГАРМОНИЧЕСКИХ ВОЗДЕЙСТВИЙ Основные характеристики гармонических сигналов Переменным током i(t) и напряжением u(t) называют токи и напряжения, изменяющиеся во времени. Сигналы, мгновенные значения которых повторяются через определенный фиксированный промежуток времени, называются периодическими, а этот промежуток времени – периодом. Такие сигналы описываются следующим образом:
где Т – период, с. Величина, обратная периоду, называется частотой
Также существует понятие угловой (циклической) частоты:
В электроэнергетике нашли широкое применение синусоидальные сигналы, как наиболее экономичные. Для передачи информации в технике связи и радиотехнике используют различные модуляции синусоидальных сигналов: амплитудную, частотную, фазовую. В общем случае любой несинусоидальный сигнал может быть представлен в виде суммы синусоидальных сигналов различной частоты с помощью разложения в ряд Фурье. И, таким образом, расчет подобных цепей может быть сведен к расчету цепей синусоидального тока и напряжения.
где
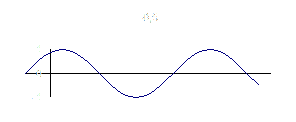
В дальнейшем под переменным сигналом будем понимать гармонический (синусоидальный) сигнал (рис. 3.1). О значениях периодических токов и напряжений обычно судят по их среднеквадратических значениях за период, которые называют действующим значением тока и напряжения и обозначают I, U:
За период Т на резисторе с сопротивлением R при синусоидальном изменении тока выделится тепловая энергия:
Таким образом, действующий ток численно равен такому постоянному току, который за время t = T выделяет в том же сопротивлении такое же количество тепла, что и переменный. В действующих величинах градуируются (тарируются) амперметры и вольтметры электродинамической и электромагнитной системы. Приборы магнитоэлектрической системы показывают постоянную составляющую тока или напряжения, или среднее значение за период:
Установим связь между действующим и амплитудным значением гармонического сигнала на примере тока. Если ток изменяется по закону
Произведя аналогичные действия для сигнала напряжения, получим
Введем понятие мощности переменного тока. Мгновенная мощность вычисляется как произведение мгновенных значений напряжения и тока
(3.10) где j – сдвиг фазы тока по отношению к напряжению,
Средняя мощность за период называется активной мощностью:
3.2. Элементы цепей гармонического тока
Электрическая цепь синусоидального тока кроме электротехнических устройств, назначение которых совпадает с назначением функционально аналогичных устройств цепи постоянного тока (источники энергии, измерительные приборы, коммутационные аппараты и др.), содержит также устройства, присущие только цепям синусоидального тока: конденсаторы и катушки индуктивности. Для расчета режима работы электротехнических устройств необходимо перейти от принципиальной схемы цепи к ее схеме замещения (математической модели). Элементами схем замещения цепей синусоидального тока являются источники синусоидальных тока и ЭДС (j (t), e (t)), резистивные (R), индуктивные (L) и емкостные (C) элементы. Рассмотрим картину распределения тока и напряжения на реальных элементах. Гармонический ток в емкости
Ток в ветви с емкостью равен скорости изменения заряда на электродах, и при указанном положительном направлении тока знак тока совпадает со знаком производной по времени от заряда q.
Единица измерения емкости – фарада (Ф). Пусть
Отсюда Емкостное сопротивление Полное сопротивление Z также равно XC. Фаза тока Таким образом, можно сделать следующие выводы: 1. Амплитуда и действующее значение напряжения и тока на емкости связаны законом Ома. 2. Напряжение uс отстает по фазе от тока iс на Мгновенная мощность
Емкостная проводимость
3.2.4. Последовательное соединение R, L, C
Для мгновенных значений токов и напряжений выполняются I и II законы Кирхгофа. При прохождении синусоидального тока
Из тригонометрии известно, что
Применим формулу (3.22) к выражению (3.21):
Реактивное сопротивление последовательной RLC – цепи
может принимать следующие значения:
Полное сопротивление цепи
угол разности фаз
определяется по оси Из выражений
что удобно представлять с помощью треугольника сопротивлений (рис. 3.10). Умножив левые и правые части выражений для сопротивлений (3.24) на действующее значение тока I, получим соответственно действующие значения напряжений на активном и реактивном сопротивлениях, которые называют активной и реактивной составляющими напряжения:
Тогда действующее значение суммарного напряжения можно определить как 3.2.5. Параллельное соединение R, L, C
Просуммируем:
Выражение (3.26) является тригонометрической формой записи I закона Кирхгофа для мгновенных значений. Активная проводимость цепи Реактивная проводимость цепи Для нахождения
т.е. ток отстает от напряжения на угол j. Здесь
Активная и реактивная проводимости цепи связаны с полной проводимостью формулами
Для проводимостей также можно построить треугольник проводимостей. Активная и реактивная составляющие тока определяются следующим образом:
Активная и реактивная составляющие тока связаны с действующим значением суммарного тока формулой Следует отметить, что описывать электрические цепи синусоидального тока, оперируя понятиями мгновенного значения тока и напряжения, достаточно трудоемко и применимо только для простейших электрических цепей, не содержащих большого числа контуров и источников. С усложнением электрических цепей такая форма расчета становится крайне затруднительной и требуется метод, позволяющий рассчитывать электрические цепи переменного тока алгебраически аналогично цепям постоянного тока. Таким удобным расчетным методом служит символический метод. Законы Ома и Кирхгофа По I закону Кирхгофа алгебраическая сумма мгновенных значений токов, сходящихся в любом узле электрической цепи, равна нулю, т.е.
В соответствии с теоремой о сумме I закон Кирхгофа в символической или комплексной форме записывается в виде
По II закону Кирхгофа алгебраическая сумма мгновенных значений падений напряжений в замкнутом контуре равна нулю, т.е.
Но в соответствии с теоремами символического метода II закон Кирхгофа в символической или комплексной форме записи имеет следующий вид:
Рассмотрим закон Ома в символической форме записи для элементов цепи гармонического тока (рис. 3.15).
На рис. 3.16 приведены векторные диаграммы напряжений и токов соответственно для сопротивления, индуктивности и емкости.
3.3.3. Последовательное соединение R, L, C
На основании теоремы о сумме
где На основании теоремы Эйлера
Полное сопротивление равно модулю полного комплексного сопротивления Комплексное сопротивление можно представить в виде
где R – действительная часть комплексного сопротивления, называется активным сопротивлением, X – мнимая часть комплексного сопротивления, называется реактивным сопротивлением, Таким образом, закон Ома в общем виде Введем понятие комплексной проводимости Для рассматриваемой цепи построим векторную диаграмму токов и напряжений. Поскольку для всех элементом общим является ток, вектор тока и выберем в качестве исходного вектора, направив его по действительной оси (рис. 3.18).
Возможны три режима работы такой цепи:
Угол j(разность начальных фаз напряжения и тока) определяется углом поворота вектора тока к вектору напряжения по кратчайшему пути: если поворот определяется против часовой стрелки, то 3.3.4. Параллельное соединение R, L, C Пусть к цепи, состоящей из параллельного соединения R, L, C элементов (рис. 3.19), приложено напряжение
Согласно теореме о сумме
Применим для каждой ветви закон Ома в комплексной форме:
Тогда где активная проводимость индуктивная проводимость емкостная проводимость На основании формулы Эйлера
Действительная часть комплексной проводимости мнимая часть комплексной проводимости Для рассматриваемой цепи построим векторную диаграмму токов и напряжений. Поскольку для всех элементом общим является напряжение
Возможны три режима работы такой цепи:
Таким образом, в параллельных ветвях характер цепи определяет большая реактивная проводимость или меньшее реактивное сопротивление. Баланс мощности Из закона сохранения энергии следует, что в любой цепи соблюдается баланс как мгновенных, так и активных мощностей. Сумма всех отдаваемых мощностей равна сумме всех получаемых мощностей. Рассмотрим, как соблюдается баланс для комплексных мощностей, а, следовательно, и для реактивных мощностей. Пусть общее число узлов схемы равно n. Запишем для каждого узла уравнение по I закону Кирхгофа для комплексных сопряженных токов:
Эти уравнения записаны в общей форме в предположении, что каждый узел (здесь узел – место соединения не менее двух ветвей) связан с остальными n – 1узлами. При отсутствии каких-либо ветвей соответствующие слагаемые в уравнениях становятся равными нулю. При наличии между какой-либо парой узлов нескольких ветвей число слагаемых соответственно увеличивается. Умножим каждое уравнение (3.59) на комплексный потенциал узла, для которого составлено уравнение:
Просуммируем все уравнения (3.60) с учетом того, что сопряженные комплексные токи входят в эти уравнения дважды (для двух различных направлений), причем
В этом выражении столько слагаемых, сколько ветвей и каждое слагаемое представляет собой комплексную мощность ветви
(3.62) При равенстве сумм комплексных величин суммы их модулей в общем случае не равны друг другу. Отсюда следует, что для полных мощностей S баланс не соблюдается. Метод контурных токов Алгоритм расчета цепей гармонического тока методом контурных токов аналогичен рассмотренному при изучении цепей постоянного тока (глава 2.3.2) с поправкой на символический метод. При решении задачи данным методом составляется система уравнений вида
где
Составим систему уравнений для контурных токов:
где
Метод узловых потенциалов Алгоритм расчета цепей гармонического тока методом узловых потенциалов аналогичен рассмотренному при изучении цепей постоянного тока (глава 2.3.3) с поправкой на символический метод. При решении задачи данным методом составляется система уравнений вида
где
Для представленной цепи на рис. 3.25 система уравнений вырождается в одно уравнение, поскольку в цепи два узла.
Метод наложения Алгоритм расчета аналогичен рассмотренному при изучении цепей постоянного тока (глава 2.3.4). Рассмотрим применение этого метода на примере схемы на рис. 3.25, которую можно заменить на две составляющие подсхемы (рис. 3.26):
ЦЕПИ С ИСТОЧНИКАМИ ГАРМОНИЧЕСКИХ ВОЗДЕЙСТВИЙ
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 824; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |

 (3.1)
(3.1)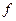 :
: . (3.2)
. (3.2)
 . (3.3)
. (3.3) , (3.4)
, (3.4)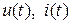 – мгновенное значение;
– мгновенное значение;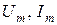 – амплитуда переменного сигнала – максимальная по модулю его величина;
– амплитуда переменного сигнала – максимальная по модулю его величина; – фаза гармонического сигнала – аргумент при синусе в каждый момент времени;
– фаза гармонического сигнала – аргумент при синусе в каждый момент времени; – начальная фаза – значение аргумента в начальный момент времени (t = 0). Фаза измеряется в радианах или градусах.
– начальная фаза – значение аргумента в начальный момент времени (t = 0). Фаза измеряется в радианах или градусах. (3.5)
(3.5)

 (3.6)
(3.6) . (3.7)
. (3.7) , то
, то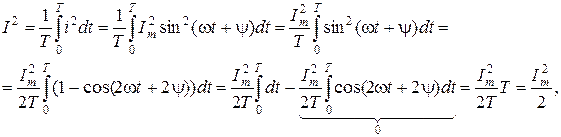
 . (3.8)
. (3.8) . (3.9)
. (3.9) Тогда
Тогда

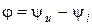 ;
; – постоянная составляющая мгновенной мощности;
– постоянная составляющая мгновенной мощности; – гармоническая составляющая, которая изменяется с двойной угловой частотой.
– гармоническая составляющая, которая изменяется с двойной угловой частотой. . (3.11)
. (3.11)
 Емкостный элемент цепи с емкостью С учитывает энергию электрического поля
Емкостный элемент цепи с емкостью С учитывает энергию электрического поля  .
. . (3.18)
. (3.18)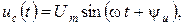 тогда
тогда . (3.19)
. (3.19)
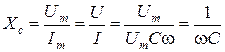 .
. , а сдвиг фаз
, а сдвиг фаз  .
. .
. .
. Мгновенная мощность может быть положительной, отрицательной и равной нулю (рис. 3.8). Если p (t)> 0, емкость заряжается энергией в виде энергии электрического поля; если p (t)< 0, емкость возвращает энергию источнику. Средняя мощность за период Pср = 0,а, следовательно, и активная мощность равна нулю, что означает, что происходит обмен энергией без потерь, емкость – реактивный элемент.
Мгновенная мощность может быть положительной, отрицательной и равной нулю (рис. 3.8). Если p (t)> 0, емкость заряжается энергией в виде энергии электрического поля; если p (t)< 0, емкость возвращает энергию источнику. Средняя мощность за период Pср = 0,а, следовательно, и активная мощность равна нулю, что означает, что происходит обмен энергией без потерь, емкость – реактивный элемент.
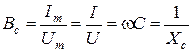 . (3.20)
. (3.20)
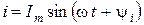 через электрическую цепь, состоящую из последовательно соединенных элементов R, L, C (рис. 3.9), на выводах a – b этой цепи создается синусоидальное напряжение, равное по II закону Кирхгофа алгебраической сумме синусоидальных напряжений на отдельных элементах:
через электрическую цепь, состоящую из последовательно соединенных элементов R, L, C (рис. 3.9), на выводах a – b этой цепи создается синусоидальное напряжение, равное по II закону Кирхгофа алгебраической сумме синусоидальных напряжений на отдельных элементах:

 (3.21)
(3.21) . (3.22)
. (3.22)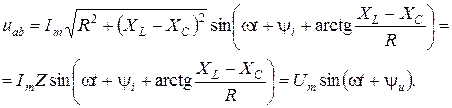 (3.23)
(3.23)
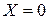 – цепь носит чисто активный характер (в цепи резонанс);
– цепь носит чисто активный характер (в цепи резонанс); – цепь носит индуктивный характер, т.е.
– цепь носит индуктивный характер, т.е.  ;
;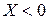 – цепь носит емкостный характер, т.е.
– цепь носит емкостный характер, т.е.  .
. ;
; ,
, от кривой напряжения к кривой тока и бывает острым или прямым: j < 0при емкостном характере цепи (ток опережает напряжение), j > 0при индуктивном характере цепи (ток отстает по фазе от напряжения), j = 0при резистивном характере цепи (индуктивное и емкостное сопротивления равны) – такой режим цепи называют резонансом напряжений.
от кривой напряжения к кривой тока и бывает острым или прямым: j < 0при емкостном характере цепи (ток опережает напряжение), j > 0при индуктивном характере цепи (ток отстает по фазе от напряжения), j = 0при резистивном характере цепи (индуктивное и емкостное сопротивления равны) – такой режим цепи называют резонансом напряжений. и
и  следует, что связь активного и реактивного сопротивления с полным сопротивлением выражается следующими формулами:
следует, что связь активного и реактивного сопротивления с полным сопротивлением выражается следующими формулами: , (3.24)
, (3.24)
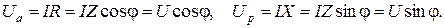 (3.25)
(3.25) Для напряжений также можно построить прямоугольный треугольник напряжений.
Для напряжений также можно построить прямоугольный треугольник напряжений. Если к выводам электрической цепи, состоящей из параллельно соединенных R, L, C (рис. 3.11), приложено синусоидальное напряжение
Если к выводам электрической цепи, состоящей из параллельно соединенных R, L, C (рис. 3.11), приложено синусоидальное напряжение  то по I закону Кирхгофа синусоидальный ток в неразветвленной части равен алгебраической сумме синусоидальных токов в параллельных ветвях
то по I закону Кирхгофа синусоидальный ток в неразветвленной части равен алгебраической сумме синусоидальных токов в параллельных ветвях 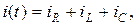 где
где – совпадает по фазе с напряжением u(t);
– совпадает по фазе с напряжением u(t); – отстает по фазе от напряжения u (t) на
– отстает по фазе от напряжения u (t) на  – опережает по фазе напряжение u (t) на
– опережает по фазе напряжение u (t) на 
 , всегда положительна.
, всегда положительна. , в зависимости от знака может иметь индуктивный (В > 0)или емкостный (B < 0)характер. Если В = 0, цепь носит активный характер.
, в зависимости от знака может иметь индуктивный (В > 0)или емкостный (B < 0)характер. Если В = 0, цепь носит активный характер.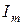 и jвоспользуемся приемом, приведенным в предыдущем разделе:
и jвоспользуемся приемом, приведенным в предыдущем разделе: , (3.27)
, (3.27) – начальная фаза напряжения;
– начальная фаза напряжения; – начальная фаза тока;
– начальная фаза тока; – разность фаз;
– разность фаз; – амплитудное значение тока;
– амплитудное значение тока; – полная проводимость цепи – величина, обратная полному сопротивлению
– полная проводимость цепи – величина, обратная полному сопротивлению  ;
; – угол разности фаз определяется по оси
– угол разности фаз определяется по оси  в направлении от напряжения к току и является острым или прямым
в направлении от напряжения к току и является острым или прямым  .
. – при индуктивном характере цепи, т.е. при B > 0; при этом ток опережает по фазе напряжение.
– при индуктивном характере цепи, т.е. при B > 0; при этом ток опережает по фазе напряжение. – при емкостном характере цепи, т.е. при B < 0; при этом ток опережает по фазе напряжение.
– при емкостном характере цепи, т.е. при B < 0; при этом ток опережает по фазе напряжение. – при резистивном характере цепи, т.е. при равенстве индуктивной и емкостной проводимостей
– при резистивном характере цепи, т.е. при равенстве индуктивной и емкостной проводимостей  ; при этом ток совпадает по фазе с напряжением. Такой режим работы электрической цепи называют резонансом токов.
; при этом ток совпадает по фазе с напряжением. Такой режим работы электрической цепи называют резонансом токов. . (3.28)
. (3.28) . (3.29)
. (3.29)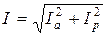 . Для токов также можно построить треугольник токов.
. Для токов также можно построить треугольник токов. .
. (3.31)
(3.31) или
или  или
или  . (3.32)
. (3.32) или
или 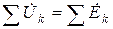 . (3.33)
. (3.33)


 ,
,  (по теореме о линейном преобразовании), то
(по теореме о линейном преобразовании), то 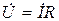 . Это закон Ома в символической форме.
. Это закон Ома в символической форме.

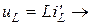
 (по теореме о производной)
Закон Ома:
(по теореме о производной)
Закон Ома:  .
.

 (по теореме об интеграле)
Закон Ома:
(по теореме об интеграле)
Закон Ома:  .
.



 По II закону Кирхгофа
По II закону Кирхгофа .
.
 , (3.34)
, (3.34) – комплексное сопротивление цепи.
– комплексное сопротивление цепи. . (3.35)
. (3.35)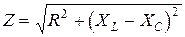 , аргумент полного комплексного сопротивления равен разности фаз напряжения и тока
, аргумент полного комплексного сопротивления равен разности фаз напряжения и тока  .
. (3.36)
(3.36)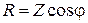 ;
; .
. , где
, где 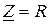 , для индуктивности
, для индуктивности  , для емкости
, для емкости 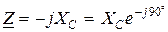 .
. . (3.37)
. (3.37)

 – индуктивный режим,
– индуктивный режим,  – резонанс напряжений,
– резонанс напряжений,  ;
; – емкостный режим,
– емкостный режим,  , которому соответствует
, которому соответствует  . Определим токи во всех ветвях.
. Определим токи во всех ветвях. По I закону Кирхгофа мгновенное значение тока
По I закону Кирхгофа мгновенное значение тока .
. .
. ,
, ,
, .
. , (3.38)
, (3.38) – полная комплексная проводимость
– полная комплексная проводимость 
 ;
; ;
; .
. . (3.39)
. (3.39) , называется активной проводимостью;
, называется активной проводимостью; , называется реактивной проводимостью.
, называется реактивной проводимостью. , вектор напряжения и выберем в качестве исходного вектора, направив его по действительной оси (рис. 3.20).
, вектор напряжения и выберем в качестве исходного вектора, направив его по действительной оси (рис. 3.20).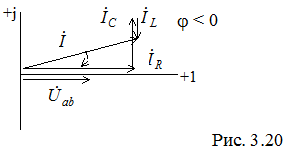

 – индуктивный режим,
– индуктивный режим, 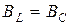 – резонанс токов,
– резонанс токов,  – емкостный режим,
– емкостный режим,  (3.59)
(3.59) (3.60)
(3.60) и т.д. В результате получим
и т.д. В результате получим (3.61)
(3.61) . Таким образом, сумма комплексных получаемых мощностей во всех ветвях равна нулю. Полученное равенство выражает баланс мощностей
. Таким образом, сумма комплексных получаемых мощностей во всех ветвях равна нулю. Полученное равенство выражает баланс мощностей  . Из него следует равенство нулю в отдельности суммы определяемых активных и суммы определяемых реактивных мощностей.
. Из него следует равенство нулю в отдельности суммы определяемых активных и суммы определяемых реактивных мощностей. Следует отметить, что взаимное направление токов и напряжений на потребителях и на источниках противоположно, как показано на рис. 3.24. Поскольку отрицательные получаемые мощности представляют собой мощности отдаваемые, то можно утверждать, что суммы всех отдаваемых и всех получаемых реактивных мощностей равны друг другу:
Следует отметить, что взаимное направление токов и напряжений на потребителях и на источниках противоположно, как показано на рис. 3.24. Поскольку отрицательные получаемые мощности представляют собой мощности отдаваемые, то можно утверждать, что суммы всех отдаваемых и всех получаемых реактивных мощностей равны друг другу:  или
или  .
. .
. , (3.63)
, (3.63)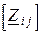 – квадратная матрица комплексных сопротивлений, в которой
– квадратная матрица комплексных сопротивлений, в которой  – собственное комплексное сопротивление,
– собственное комплексное сопротивление, – общее комплексное сопротивление i и j контуров;
– общее комплексное сопротивление i и j контуров; – матрица-столбец контурных токов;
– матрица-столбец контурных токов;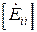 – матрица-столбец контурных ЭДС.
– матрица-столбец контурных ЭДС. Пример. В цепи на рис. 3.25 гармонические источники ЭДС
Пример. В цепи на рис. 3.25 гармонические источники ЭДС



 , (3.63)
, (3.63) – квадратная матрица комплексных проводимостей, в которой
– квадратная матрица комплексных проводимостей, в которой  – собственная комплексная проводимость,
– собственная комплексная проводимость,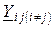 – общая комплексная проводимость ветвей, соединяющих i и j узлы;
– общая комплексная проводимость ветвей, соединяющих i и j узлы; – матрица-столбец потенциалов;
– матрица-столбец потенциалов; – матрица-столбец узловых токов.
– матрица-столбец узловых токов.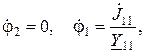





 .
.



