
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гармонический ток в сопротивленииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Тогда ток в сопротивлении R (рис. 3.3) можно определить по закону Ома:
Отсюда Сдвиг фаз между напряжением и током Поскольку
где Z – полное сопротивление цепи (импеданс), равное отношению действующих значений напряжения и тока. Для цепи, представленной на рис. 3.3, полное сопротивление Для определения мгновенной мощности, поступающей в сопротивление, воспользуемся полученным выше соотношением для мгновенной мощности:
Активная мощность, равная средней мощности за период,
Таким образом, в резистивном элементе с сопротивлением R электромагнитная энергия преобразуется в тепловую при мощности преобразования
Индуктивность – элемент цепи, который учитывает энергию магнитного поля При изменении тока в индуктивности возникает ЭДС самоиндукции eL. По закону Ленца eL препятствует изменению тока. Поэтому при традиционном выборе одинаковых положительных направлений для тока iL и ЭДС eL, как показано на рис. 3.5, знаки eL и где L – коэффициент пропорциональности, называемый индуктивностью. Единица измерения индуктивности – генри (Гн). Так как электрическому току всегда сопутствует магнитное поле, любой обтекаемый током участок цепи, представляющий электротехническое устройство, должен характеризоваться индуктивностью. Если
Закон Ома для цепи с индуктивным элементом
Начальная фаза напряжения Таким образом, можно сделать следующие выводы: 1. Амплитуда и действующее значение напряжения и тока на индуктивности связаны законом Ома. 2. Напряжение uL опережает по фазе ток iL на Мгновенная мощность
Из выражения (3.16) следует, что средняя мощность за период, а следовательно, и активная мощность равны нулю. Индуктивность – реактивный элемент. Мгновенная мощность может быть положительной, отрицательной и равной нулю (рис. 3.6). Если p (t)> 0, индуктивность заряжается энергией
в виде энергии магнитного поля; если p (t)< 0,индуктивность возвращает энергию источнику. Средняя мощность за период P ср= 0(мгновенная мощность колеблется относительно нуля). Индуктивная проводимость
Гармонический ток в емкости
Ток в ветви с емкостью равен скорости изменения заряда на электродах, и при указанном положительном направлении тока знак тока совпадает со знаком производной по времени от заряда q.
Единица измерения емкости – фарада (Ф). Пусть
Отсюда Емкостное сопротивление Полное сопротивление Z также равно XC. Фаза тока Таким образом, можно сделать следующие выводы: 1. Амплитуда и действующее значение напряжения и тока на емкости связаны законом Ома. 2. Напряжение uс отстает по фазе от тока iс на Мгновенная мощность
Емкостная проводимость
3.2.4. Последовательное соединение R, L, C
Для мгновенных значений токов и напряжений выполняются I и II законы Кирхгофа. При прохождении синусоидального тока
Из тригонометрии известно, что
Применим формулу (3.22) к выражению (3.21):
Реактивное сопротивление последовательной RLC – цепи
может принимать следующие значения:
Полное сопротивление цепи
угол разности фаз
определяется по оси Из выражений
что удобно представлять с помощью треугольника сопротивлений (рис. 3.10). Умножив левые и правые части выражений для сопротивлений (3.24) на действующее значение тока I, получим соответственно действующие значения напряжений на активном и реактивном сопротивлениях, которые называют активной и реактивной составляющими напряжения:
Тогда действующее значение суммарного напряжения можно определить как 3.2.5. Параллельное соединение R, L, C
Просуммируем:
Выражение (3.26) является тригонометрической формой записи I закона Кирхгофа для мгновенных значений. Активная проводимость цепи Реактивная проводимость цепи Для нахождения
т.е. ток отстает от напряжения на угол j. Здесь
Активная и реактивная проводимости цепи связаны с полной проводимостью формулами
Для проводимостей также можно построить треугольник проводимостей. Активная и реактивная составляющие тока определяются следующим образом:
Активная и реактивная составляющие тока связаны с действующим значением суммарного тока формулой Следует отметить, что описывать электрические цепи синусоидального тока, оперируя понятиями мгновенного значения тока и напряжения, достаточно трудоемко и применимо только для простейших электрических цепей, не содержащих большого числа контуров и источников. С усложнением электрических цепей такая форма расчета становится крайне затруднительной и требуется метод, позволяющий рассчитывать электрические цепи переменного тока алгебраически аналогично цепям постоянного тока. Таким удобным расчетным методом служит символический метод.
|
|||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 758; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.34.51 (0.007 с.) |

 Пусть
Пусть 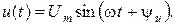
 ,
,
 .
.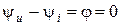 , т.е. ток и напряжение на сопротивлении совпадают по фазе.
, т.е. ток и напряжение на сопротивлении совпадают по фазе. , то для действующих значений справедливо
, то для действующих значений справедливо , (3.11)
, (3.11) .
.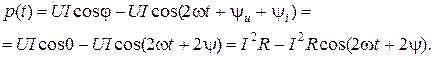 (3.12)
(3.12) (3.13)
(3.13)
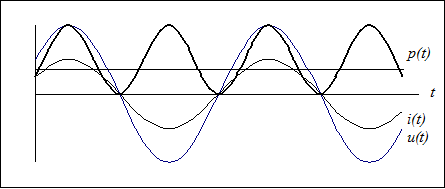
 Резистивные элементы вводят в схему также и для учета необратимого преобразования электромагнитной энергии в другие формы энергии (например, в механическую) и для учета излучаемой энергии.
Резистивные элементы вводят в схему также и для учета необратимого преобразования электромагнитной энергии в другие формы энергии (например, в механическую) и для учета излучаемой энергии.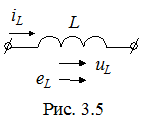 Гармонический ток в индуктивности
Гармонический ток в индуктивности . При увеличении (уменьшении) тока энергия магнитного поля увеличивается (уменьшается). Следовательно, индуктивные элементы можно рассматривать как аккумуляторы (накопители энергии).
. При увеличении (уменьшении) тока энергия магнитного поля увеличивается (уменьшается). Следовательно, индуктивные элементы можно рассматривать как аккумуляторы (накопители энергии). противоположны и
противоположны и 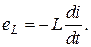 Чтобы через индуктивность проходил переменный ток, к ее выводам надо приложить напряжение uL, равное по величине и противоположное по направлению ЭДС eL:
Чтобы через индуктивность проходил переменный ток, к ее выводам надо приложить напряжение uL, равное по величине и противоположное по направлению ЭДС eL: (3.14)
(3.14) тогда
тогда (3.15)
(3.15) .
.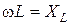 – индуктивное сопротивление, имеет размерность сопротивления. Полное сопротивление Z также равно XL.
– индуктивное сопротивление, имеет размерность сопротивления. Полное сопротивление Z также равно XL. , сдвиг фаз
, сдвиг фаз  .
. .
. (3.16)
(3.16)

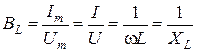 . (3.17)
. (3.17) Емкостный элемент цепи с емкостью С учитывает энергию электрического поля
Емкостный элемент цепи с емкостью С учитывает энергию электрического поля  .
. . (3.18)
. (3.18)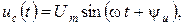 тогда
тогда . (3.19)
. (3.19)
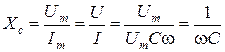 .
. , а сдвиг фаз
, а сдвиг фаз  .
. .
. Мгновенная мощность может быть положительной, отрицательной и равной нулю (рис. 3.8). Если p (t)> 0, емкость заряжается энергией в виде энергии электрического поля; если p (t)< 0, емкость возвращает энергию источнику. Средняя мощность за период Pср = 0,а, следовательно, и активная мощность равна нулю, что означает, что происходит обмен энергией без потерь, емкость – реактивный элемент.
Мгновенная мощность может быть положительной, отрицательной и равной нулю (рис. 3.8). Если p (t)> 0, емкость заряжается энергией в виде энергии электрического поля; если p (t)< 0, емкость возвращает энергию источнику. Средняя мощность за период Pср = 0,а, следовательно, и активная мощность равна нулю, что означает, что происходит обмен энергией без потерь, емкость – реактивный элемент.
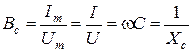 . (3.20)
. (3.20)
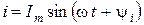 через электрическую цепь, состоящую из последовательно соединенных элементов R, L, C (рис. 3.9), на выводах a – b этой цепи создается синусоидальное напряжение, равное по II закону Кирхгофа алгебраической сумме синусоидальных напряжений на отдельных элементах:
через электрическую цепь, состоящую из последовательно соединенных элементов R, L, C (рис. 3.9), на выводах a – b этой цепи создается синусоидальное напряжение, равное по II закону Кирхгофа алгебраической сумме синусоидальных напряжений на отдельных элементах:

 (3.21)
(3.21) . (3.22)
. (3.22)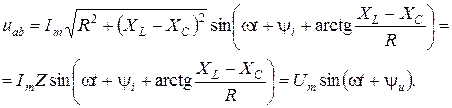 (3.23)
(3.23)
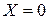 – цепь носит чисто активный характер (в цепи резонанс);
– цепь носит чисто активный характер (в цепи резонанс); – цепь носит индуктивный характер, т.е.
– цепь носит индуктивный характер, т.е.  ;
;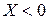 – цепь носит емкостный характер, т.е.
– цепь носит емкостный характер, т.е.  .
. ;
; ,
, от кривой напряжения к кривой тока и бывает острым или прямым: j < 0при емкостном характере цепи (ток опережает напряжение), j > 0при индуктивном характере цепи (ток отстает по фазе от напряжения), j = 0при резистивном характере цепи (индуктивное и емкостное сопротивления равны) – такой режим цепи называют резонансом напряжений.
от кривой напряжения к кривой тока и бывает острым или прямым: j < 0при емкостном характере цепи (ток опережает напряжение), j > 0при индуктивном характере цепи (ток отстает по фазе от напряжения), j = 0при резистивном характере цепи (индуктивное и емкостное сопротивления равны) – такой режим цепи называют резонансом напряжений. и
и  следует, что связь активного и реактивного сопротивления с полным сопротивлением выражается следующими формулами:
следует, что связь активного и реактивного сопротивления с полным сопротивлением выражается следующими формулами: , (3.24)
, (3.24)
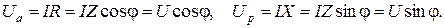 (3.25)
(3.25) Для напряжений также можно построить прямоугольный треугольник напряжений.
Для напряжений также можно построить прямоугольный треугольник напряжений. Если к выводам электрической цепи, состоящей из параллельно соединенных R, L, C (рис. 3.11), приложено синусоидальное напряжение
Если к выводам электрической цепи, состоящей из параллельно соединенных R, L, C (рис. 3.11), приложено синусоидальное напряжение  то по I закону Кирхгофа синусоидальный ток в неразветвленной части равен алгебраической сумме синусоидальных токов в параллельных ветвях
то по I закону Кирхгофа синусоидальный ток в неразветвленной части равен алгебраической сумме синусоидальных токов в параллельных ветвях 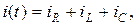 где
где – совпадает по фазе с напряжением u(t);
– совпадает по фазе с напряжением u(t); – отстает по фазе от напряжения u (t) на
– отстает по фазе от напряжения u (t) на  – опережает по фазе напряжение u (t) на
– опережает по фазе напряжение u (t) на 
 , всегда положительна.
, всегда положительна. , в зависимости от знака может иметь индуктивный (В > 0)или емкостный (B < 0)характер. Если В = 0, цепь носит активный характер.
, в зависимости от знака может иметь индуктивный (В > 0)или емкостный (B < 0)характер. Если В = 0, цепь носит активный характер.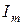 и jвоспользуемся приемом, приведенным в предыдущем разделе:
и jвоспользуемся приемом, приведенным в предыдущем разделе: , (3.27)
, (3.27) – начальная фаза напряжения;
– начальная фаза напряжения; – начальная фаза тока;
– начальная фаза тока; – разность фаз;
– разность фаз; – амплитудное значение тока;
– амплитудное значение тока; – полная проводимость цепи – величина, обратная полному сопротивлению
– полная проводимость цепи – величина, обратная полному сопротивлению  ;
; – угол разности фаз определяется по оси
– угол разности фаз определяется по оси  в направлении от напряжения к току и является острым или прямым
в направлении от напряжения к току и является острым или прямым  .
. – при индуктивном характере цепи, т.е. при B > 0; при этом ток опережает по фазе напряжение.
– при индуктивном характере цепи, т.е. при B > 0; при этом ток опережает по фазе напряжение. – при емкостном характере цепи, т.е. при B < 0; при этом ток опережает по фазе напряжение.
– при емкостном характере цепи, т.е. при B < 0; при этом ток опережает по фазе напряжение. – при резистивном характере цепи, т.е. при равенстве индуктивной и емкостной проводимостей
– при резистивном характере цепи, т.е. при равенстве индуктивной и емкостной проводимостей  ; при этом ток совпадает по фазе с напряжением. Такой режим работы электрической цепи называют резонансом токов.
; при этом ток совпадает по фазе с напряжением. Такой режим работы электрической цепи называют резонансом токов. . (3.28)
. (3.28) . (3.29)
. (3.29)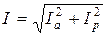 . Для токов также можно построить треугольник токов.
. Для токов также можно построить треугольник токов.


