Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Производные: постоянной, суммы, произведения, частногоСодержание книги
Поиск на нашем сайте
Теорема 2. Если y = c, где c = const, то y' = 0. Доказательство Функция y = c принимает значение, равное c для любого аргумента x. Таким образом, Δy = 0 при любом x. Следовательно,
Теорема доказана. Теорема3. Пустьфункции u=u(x), v=v(x) дифференцируемы. Тогда Доказательство Если аргумент x получит приращение Δx, то функции u, v получат приращения
Пусть y=u+v, тогда Воспользовавшись свойством предела суммы функции, получаем
Утверждение 1) теоремы доказано. Если y = u v, то
Утверждение 2) теоремы доказано. Теперь, если Прибавив и отняв в правой части этого равенства частное
Далее аналогично доказываем утверждение 3). Теорема доказана. Из теорем 2,3 следует, что постоянную можно выносить за знак производной, т.е. (cy)' = cy' Производная произведения функций. Пусть u(x) и u(x) - дифференцируемые функции. Тогда произведение функций u(x)v(x) также дифференцируемо и
Внимание:
Пусть u(x) и u(x) - дифференцируемые функции. Тогда, если v(x) ≠ 0, то производная частного этих функций вычисляется по формуле
59) Теорема.О производной обратной функции. Если функция y=f(x) дифференцируема в т. х0 и $ обратная к ней функция x=j(y), которая непрерывна в т. y0=f(х0), то обратная функция дифференцируема в т. y0, причем j'y Доказательство. Очевидно, что Dj=Dх (обратная функция непрерывна).Значит
. Если Dх®0, то Dy®0, а поэтому , то есть j'y, что и требовалось доказать. Пример. Пусть y= arcsin x, тогда x= sin y- обратная ê y= arcsin х. Так как , а, то для производной функции y= arcsin x имеем , где учтено что при yÎ[-p/2,p/2], cos y³0. Используя рассмотренные ранее теоремы для других обратных тригонометрических функций имеем: arccos x =p/2- arcsin x и поэтому (arccos x)'=-, y= arctg x, x= tg y, а значит (arctg x)'=, (arcctg x)'=-
60)
Данная формула показывает, что производная сложной функции равна произведению производной внешней функции на производную от внутренней функции. Важно, однако, что производная внутренней функции вычисляется в точке x, а производная внешней функции - вточке u=g(x)! Эта формула легко обобщается на случай, когда сложная функция состоит из нескольких "слоев", вложенных иерархически друг в друга. Рассмотрим несколько примеров, иллюстрирующих правило производной сложной функции. Это правило широко применяется и во многих других задачах раздела "Дифференцирование".
|
|||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 1440; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.15.18 (0.006 с.) |





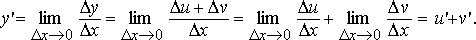
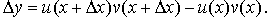 Прибавив и отняв в правой части этого равенства произведение
Прибавив и отняв в правой части этого равенства произведение  , после перегруппировки слагаемых получим
, после перегруппировки слагаемых получим 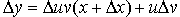 . Воспользовавшись свойствами предела функции, получаем
. Воспользовавшись свойствами предела функции, получаем

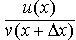 , после перегруппировки слагаемых получим
, после перегруппировки слагаемых получим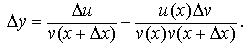
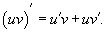

 где u = g(x) - внутренняя функция, являющаяся, в свою очередь, аргументом для внешней функции f. Если f и g - дифференцируемые функции, то сложная функция
где u = g(x) - внутренняя функция, являющаяся, в свою очередь, аргументом для внешней функции f. Если f и g - дифференцируемые функции, то сложная функция 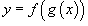 также дифференцируема по x и ее производная равна
также дифференцируема по x и ее производная равна