
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Евклидовы и унитарные пространства.Содержание книги
Поиск на нашем сайте
Понятие Будем говорить, что в I. II. III. IV. Если
Отметим, что из III при
т. е. скалярное произведение нулевого вектора на любой вектор Из II и III немедленно вытекает следующая формула для скалярного произведения и линейных комбинаций двух систем векторов:
Если в УТВЕРЖДЕНИЕ 1. При любом ДОКАЗАТЕЛЬСТВО. В самом деле, возьмем в пространстве
то положим
Легко проверяется, что условия I - IV будут выполнены, т. е. равенство (1) определяет в пространстве Мы видим, что в Пусть дано произвольное
Из (1) следует, что нулевой вектор ортогонален к любому вектору; могут существовать, однако, и ненулевые ортогональные векторы. Система векторов называется ортогональной системой, если все векторы этой системы попарно ортогональны между собой. ТЕОРЕМА 1. Всякая ортогональная система ненулевых векторов линейно независима. ДОКАЗАТЕЛЬСТВО. Пусть, в самом деле, в
Если
то, скалярно умножая обе части этого равенства на вектор
Отсюда, так как Опишем далее так называемый процесс ортогонализации, т. е. некоторый способ перехода от любой линейно независимой системы из Положим
Так как
откуда, ввиду IV,
Пусть уже построена ортогональная система ненулевых векторов
Вектор
отсюда, так как векторы
т. е.
Продолжая этот процесс, мы построим искомую ортогональную систему Применяя процесс ортогонализации к произвольному базису пространства УТВЕРЖДЕНИЕ 2. Всякое евклидово пространство обладает ортогональными базисами, причем любой ненулевой вектор этого пространства входит в состав некоторого ортогонального базиса. □ В дальнейшем важную роль будет играть один специальный вид ортогональных базисов; базисы этого вида соответствуют прямоугольным декартовым системам координат, используемым в аналитической геометрии. Назовем вектор Если
Вектор
Базис
Пример 1. Привести систему векторов
к ортонормированному виду. Решение. Применим к указанным векторам процесс ортогонализации.
Осталось нормировать систему
Итак,
УТВЕРЖДЕНИЕ 3. Всякое евклидово пространство обладает ортонормированными базисами. ДОКАЗАТЕЛЬСТВО. Достаточно взять любой ортогональный базис и нормировать все его векторы. Базис останется при этом ортогональным, так как при любых
ТЕОРЕМА 2. Базис
следует
ДОКАЗАТЕЛЬСТВО. Действительно, если для нашего базиса выполняются равенства (4), то
Обратно, если наш базис таков, что для любых векторов Сопоставляя полученный сейчас результат с изложенным ранее доказательством существования УТВЕРЖДЕНИЕ 4. Если в Евклидовы пространства 1) это соответствие является изоморфным соответствием между 2) при этом соответствии сохраняется скалярное произведение; иными словами, если образами векторов
Из условия 1) сразу следует, что изоморфные евклидовы пространства имеют одну и ту же размерность. Докажем обратное утверждение: ТЕОРЕМА 3. Любые евклидовы пространства ДОКАЗАТЕЛЬСТВО. В самом деле, выберем в пространствах Ставя в соответствие всякому вектору
то, в силу (6):
Естественно изоморфные евклидовы пространства не считать различными. Поэтому для всякого На случай комплексных линейных пространств понятия и результаты настоящего параграфа переносятся следующим образом. Комплексное линейное пространство I '. где черта над скалярным произведением обозначает, как обычно, переход к сопряженному комплексному числу. Следовательно, скалярное произведение в унитарном пространстве не будет коммутативным. Тем не менее, равенство, симметричное аксиоме II, остается справедливым. II '. так как III '. так как IV '. Скалярный квадрат ненулевого вектора
Понятия ортогональности и ортонормированной системы векторов переносятся на случай унитарных пространств без всяких изменений. Как и выше, доказывается существование ортонормированных базисов во всяком конечномерном унитарном пространстве. При этом, однако, если
Пусть ТЕОРЕМА 4. Для любых двух векторов
причем равенство достигается лишь в случае, когда векторы ДОКАЗАТЕЛЬСТВО. Достаточно доказать это неравенство для векторов, отличных от нуля. Рассмотрим
Положим
Учитывая, что
Если Из неравенства Коши - Буняковского легко вытекает так называемое «неравенство треугольника для векторов», а именно:
Действительно,
где
Величиной угла между двумя отличными от нуля векторами
Из неравенства Коши - Буняковского следует, что угол
|
||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 466; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.23.101.75 (0.011 с.) |

 мерного линейного пространства
мерного линейного пространства  , данное в § 3.1 [1], далеко не в полной мере обобщает понятия плоскости или трехмерного евклидова пространства: в
, данное в § 3.1 [1], далеко не в полной мере обобщает понятия плоскости или трехмерного евклидова пространства: в  определено скалярное умножение, если всякой паре векторов
определено скалярное умножение, если всякой паре векторов  поставлено в соответствие действительное число, обозначаемое символом
поставлено в соответствие действительное число, обозначаемое символом  и называемое скалярным произведением векторов
и называемое скалярным произведением векторов  и
и 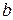 , причем выполняются следующие условия (здесь
, причем выполняются следующие условия (здесь  любые векторы пространства
любые векторы пространства  любое действительное число):
любое действительное число):


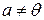 , то скалярный квадрат вектора
, то скалярный квадрат вектора 
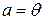 следует равенство
следует равенство (1)
(1)
 в
в  . Если
. Если
 (2)
(2) ,т. е. в
,т. е. в 
 причем
причем  и
и (3)
(3)
 получаем:
получаем:
 по IV, вытекает
по IV, вытекает  что и требовалось доказать. □
что и требовалось доказать. □ векторов
векторов  евклидова пространства
евклидова пространства  .
. , т. е. первый вектор системы (
, т. е. первый вектор системы (
 и
и  линейно независимы, то вектор
линейно независимы, то вектор  отличен от нуля при любом числе
отличен от нуля при любом числе  . Подберем это число из условии, что вектор
. Подберем это число из условии, что вектор  :
:

 ; дополнительно предположим, что для всякого
; дополнительно предположим, что для всякого  вектор
вектор  является линейной комбинацией векторов
является линейной комбинацией векторов  Это предположение будет выполняться тогда и для вектора
Это предположение будет выполняться тогда и для вектора  если он будет выбран в виде
если он будет выбран в виде
 не входит в записи векторов
не входит в записи векторов  подберем из условия, что вектор
подберем из условия, что вектор 




 , то нормированием вектора
, то нормированием вектора 

 евклидова пространства
евклидова пространства  (4)
(4)
 Вектор
Вектор  Подставляя значения, получим
Подставляя значения, получим  Далее ищем
Далее ищем  Здесь
Здесь  После подстановки, имеем:
После подстановки, имеем: 
 .
.


 искомая ортонормированная система.
искомая ортонормированная система. и
и  из
из  следует
следует □
□ (5)
(5)
 и
и  , различные или одинаковые, мы из (6) выведем равенства (4). □
, различные или одинаковые, мы из (6) выведем равенства (4). □ и
и  называются изоморфными, если между векторами этих пространств можно установить такое взаимно однозначное соответствие, что выполняются следующие требования:
называются изоморфными, если между векторами этих пространств можно установить такое взаимно однозначное соответствие, что выполняются следующие требования: и
и  из
из  (7)
(7) .
. из
из  из
из 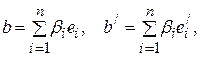
 .□
.□ называется унитарным пространством, если в нем задано скалярное умножение, причем
называется унитарным пространством, если в нем задано скалярное умножение, причем  будет комплексным числом; при этом должны выполняться аксиомы II - IV, а аксиома I заменяется следующей аксиомой:
будет комплексным числом; при этом должны выполняться аксиомы II - IV, а аксиома I заменяется следующей аксиомой:




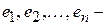 ортонормированный базис и векторы
ортонормированный базис и векторы 
 элемент унитарного пространства
элемент унитарного пространства 
 называется длиной вектора
называется длиной вектора  мерного унитарного пространства
мерного унитарного пространства 
 . Преобразовывая левую часть, получим
. Преобразовывая левую часть, получим .
. , после подстановки в неравенство и домножения на
, после подстановки в неравенство и домножения на  , получим
, получим .
. , имеем
, имеем .
. , т. е.
, т. е.  .
. ,
, целая часть комплексного числа
целая часть комплексного числа  , то
, то . □
. □ ,
,  , определенное условием
, определенное условием
 (т. е. векторы
(т. е. векторы  .
.


