
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Положительно определенные формы.Содержание книги
Поиск на нашем сайте Квадратичная форма ТЕОРЕМА. 1. Квадратичная форма ДОКАЗАТЕЛЬСТВО. Пусть форма
причем
с отличным от нуля определителем из действительных коэффициентов
обладает ненулевым решением, хотя её определитель отличен от нуля. Подставляя найденные для Обратно, пусть форма Покажем, что в этом случае можно подобрать такие действительные значения для неизвестных С помощью доказанной теоремы нельзя, к сожалению, по коэффициентам формы установить, будет ли эта форма положительно определенной. Для этой цели служит другая теорема, которую мы сформулируем и докажем после того, как введем одно вспомогательное понятие. Пусть дана квадратичная форма
из которых последний совпадает, очевидно, с определителем матрицы ЛЕММА. Если квадратичная форма ДОКАЗАТЕЛЬСТВО. Действительно, после преобразования мы получаем квадратичную форму с матрицей
т. е. определитель ТЕОРЕМА. 2. Квадратичная форма ДОКАЗАТЕЛЬСТВО. Воспользуемся индукцией по количеству неизвестных. При Пусть дана квадратичная форма
Ее можно записать в виде
где Главные миноры формы Пусть форма Пусть теперь строго положительны все главные миноры формы
точные выражения коэффициентов
то невырожденное линейное преобразование
приводит, ввиду (4), форму
Для доказательства положительной определенности формы Пример 3. Квадратичная форма
положительно определена, так как ее главные миноры
положительны. Пример 4. Квадратичная форма
не будет положительно определенной, так как ее второй главный минор отрицателен:
По аналогии с положительно определенными квадратичными формами можно ввести отрицательно определенные формы, т. е. такие невырожденные квадратичные формы с действительными коэффициентами, нормальный вид которых содержит лишь отрицательные квадраты неизвестных. Вырожденные квадратичные формы, нормальный вид которых состоит из квадратов одного знака, называются иногда полуопределенными. Наконец, неопределенными будут такие квадратичные формы, нормальный вид которых содержит как положительные, так и отрицательные квадраты неизвестных.
Пары форм.
Пусть дана пара действительных квадратичных форм от В общем случае ответ будет отрицательным. Рассмотрим, например, пару форм
Пусть существует невырожденное линейное преобразование
приводящее обе эти формы к каноническому виду. Для того чтобы форма
Так как форма Ситуация будет иной, если мы положим, что хотя бы одна из наших форм, например ТЕОРЕМА. Если ДОКАЗАТЕЛЬСТВО. Выполним сначала невырожденное линейное преобразование неизвестных
приводящее положительно определенную форму
Форма
Совершим теперь ортогональное преобразование неизвестных
приводящее форму
Это преобразование переводит сумму квадратов неизвестных
т. е. линейное преобразование
является искомым. □
ЗАДАЧИ К ГЛАВЕ II. 15. Записать матрицу квадратичной формы а) б) в) г) д) е) ж) з) и) к) 16. Записать квадратичную форму а) б) в) г) д) е) 17. Определить ранг квадратичной формы а) б) в) г) д) 18. Привести к каноническому виду квадратичную форму а) б) в) г) д) е) 19. Найти ортогональное преобразование, приводящее квадратичную форму а) б) в) г) д) е) ж) з) и) к) л) м) 20. Исследовать на знакоопределённость каждую из данных квадратичных форм: а) б) в) г) д) е) 21. Исследовать, при каких значениях а) б) в) г) д) е) ж)
|
||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 492; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 от
от  неизвестных с действительными коэффициентами называется положительно определенной, если она приводится к нормальному виду, состоящему из
неизвестных с действительными коэффициентами называется положительно определенной, если она приводится к нормальному виду, состоящему из  с действительными коэффициентами тогда и только тогда будет положительно определенной, когда при всяких действительных значениях этих неизвестных, хотя бы одно из которых отлично от нуля, эта форма получает положительные значения.
с действительными коэффициентами тогда и только тогда будет положительно определенной, когда при всяких действительных значениях этих неизвестных, хотя бы одно из которых отлично от нуля, эта форма получает положительные значения. , (1)
, (1) (2)
(2) . Подставим в
. Подставим в 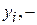 в (1). Заметим, что значения, полученные для
в (1). Заметим, что значения, полученные для  из (2), не могут все сразу равняться нулю, так как иначе мы получили бы, что система линейных однородных уравнений
из (2), не могут все сразу равняться нулю, так как иначе мы получили бы, что система линейных однородных уравнений ,
, , или отсутствует совсем, или же содержится со знаком минус.
, или отсутствует совсем, или же содержится со знаком минус.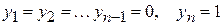 . Действительно, при этих значениях неизвестных
. Действительно, при этих значениях неизвестных  не входит в нормальный вид этой формы, и равна
не входит в нормальный вид этой формы, и равна  , если
, если  . Миноры порядка
. Миноры порядка  этой матрицы, расположенные в ее левом верхнем углу, т. е. миноры
этой матрицы, расположенные в ее левом верхнем углу, т. е. миноры ,
, , называются главными минорами формы
, называются главными минорами формы 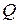 , то знак определителя формы (т. е. определителя ее матрицы) не меняется.
, то знак определителя формы (т. е. определителя ее матрицы) не меняется. , однако, ввиду
, однако, ввиду 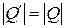 ,
,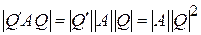 ,
, умножается на положительное число. □
умножается на положительное число. □ теорема верна, так как форма имеет в этом случае вид
теорема верна, так как форма имеет в этом случае вид  и поэтому положительно определена тогда и только тогда, если
и поэтому положительно определена тогда и только тогда, если 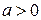 . Будем, поэтому доказывать теорему для случая
. Будем, поэтому доказывать теорему для случая  неизвестных она уже доказана.
неизвестных она уже доказана.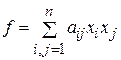 .
. , (3)
, (3) будет квадратичной формой от
будет квадратичной формой от  .
. не все равные нулю, при которых форма
не все равные нулю, при которых форма  , мы получили бы, ввиду (3), также не строго положительное значение формы
, мы получили бы, ввиду (3), также не строго положительное значение формы  . Это линейное преобразование можно дополнить до (невырожденного) линейного преобразования всех неизвестных
. Это линейное преобразование можно дополнить до (невырожденного) линейного преобразования всех неизвестных 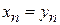 . Ввиду (3) форма
. Ввиду (3) форма  (4)
(4) для нас несущественны. Так как
для нас несущественны. Так как

 (5)
(5) . Определитель формы, стоящей в правой части равенства (5), равен
. Определитель формы, стоящей в правой части равенства (5), равен 



 и
и  . Существует ли такое невырожденное линейное преобразование неизвестных
. Существует ли такое невырожденное линейное преобразование неизвестных  , которое одновременно приводило бы обе эти формы к каноническому виду?
, которое одновременно приводило бы обе эти формы к каноническому виду? .
.
 должен быть равен нулю, иначе вошло бы слагаемое
должен быть равен нулю, иначе вошло бы слагаемое  . Меняя, если нужно, нумерацию неизвестных
. Меняя, если нужно, нумерацию неизвестных  , можно положить, что
, можно положить, что  и поэтому
и поэтому  . Мы получим теперь, однако, что
. Мы получим теперь, однако, что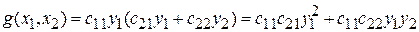 .
. также должна была перейти в канонический вид, то
также должна была перейти в канонический вид, то  , т. е.
, т. е.  , что вместе с
, что вместе с  , является положительно определенной.
, является положительно определенной. пара действительных квадратичных форм от
пара действительных квадратичных форм от  ,
, ,
, .
. .
. ,
, ,
, .
. (что следует из формулы
(что следует из формулы  ). В результате мы получаем
). В результате мы получаем ,
,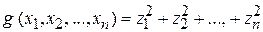 .
.
 , если:
, если: ;
;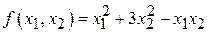 ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; .
. по заданной матрице
по заданной матрице 





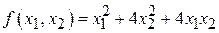 ;
; ;
; ;
; ;
; .
. ;
;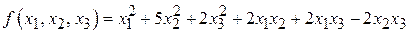 ;
; ;
; ;
; ;
; .
. ;
;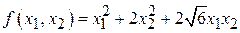 ;
; ;
; ;
; ;
;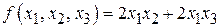 ;
;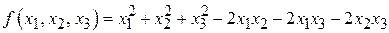 ;
; ;
; ;
; ;
; ;
; .
. ;
; ;
; ;
; ;
; ;
; .
.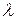 является знакоопределённой каждая из данных квадратичных форм:
является знакоопределённой каждая из данных квадратичных форм: ;
; ;
; ;
; ;
; ;
; ;
; .
.


