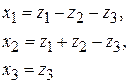Приведение квадратичной формы к каноническому виду.
Похожие статьи вашей тематики
Теория квадратичных форм берёт своё начало в аналитической геометрии, а именно в теории кривых второго порядка. Известно, что уравнение центральной кривой второго порядка на плоскости, после перенесения начала прямоугольных координат в центр этой кривой, имеет вид
 . (1) . (1)
Известно, далее, что можно совершить такой поворот осей координат на некоторый угол  (величина которого зависит от коэффициентов (величина которого зависит от коэффициентов  ), т.е. такой переход от координат ), т.е. такой переход от координат  к координатам к координатам  : :
 (2) (2)
что в новых координатах уравнение нашей кривой будет иметь «канонический» вид
 , (3) , (3)
в этом уравнении коэффициент при произведении неизвестных  равен, следовательно, нулю. Преобразование координат (2) можно толковать, очевидно, как линейное преобразование неизвестных, притом невырожденное, так как определитель из его коэффициентов равен единице. Это преобразование применяется к левой части уравнения (1), и поэтому можно сказать, что левая часть уравнения (1) невырожденным линейным преобразованием (2) превращается в левую часть уравнения (3). равен, следовательно, нулю. Преобразование координат (2) можно толковать, очевидно, как линейное преобразование неизвестных, притом невырожденное, так как определитель из его коэффициентов равен единице. Это преобразование применяется к левой части уравнения (1), и поэтому можно сказать, что левая часть уравнения (1) невырожденным линейным преобразованием (2) превращается в левую часть уравнения (3).
Рассмотрим общий случай, когда число неизвестных вместо двух равно любому  , а коэффициенты являются или действительными, или же любыми комплексными числами. , а коэффициенты являются или действительными, или же любыми комплексными числами.
Обобщая выражение, состоящее в левой части уравнения (1), приходим к следующему понятию.
Квадратичной формой  от от  неизвестных неизвестных  называется сумма, каждое слагаемое которой является или квадратом одного из этих неизвестных, или произведением двух разных неизвестных. Квадратичная форма называется действительной или комплексной в зависимости от того, являются ли ее коэффициенты действительными или же могут быль любыми комплексными числами. называется сумма, каждое слагаемое которой является или квадратом одного из этих неизвестных, или произведением двух разных неизвестных. Квадратичная форма называется действительной или комплексной в зависимости от того, являются ли ее коэффициенты действительными или же могут быль любыми комплексными числами.
Считая, что в квадратичной форме  уже сделано приведение подобных слагаемых, введем следующие обозначения для коэффициентов этой формы: коэффициент при уже сделано приведение подобных слагаемых, введем следующие обозначения для коэффициентов этой формы: коэффициент при 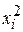 обозначим через обозначим через  , а коэффициент при произведении , а коэффициент при произведении  для для  через через  . Так как, однако, . Так как, однако,  , то коэффициент при этом произведении мог бы быть обозначен и через , то коэффициент при этом произведении мог бы быть обозначен и через  , т.е. введенные нами обозначения предполагают справедливость равенства , т.е. введенные нами обозначения предполагают справедливость равенства
 . (4) . (4)
Слагаемое  можно записать теперь в виде можно записать теперь в виде 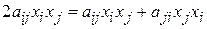 , а всю квадратичную форму , а всю квадратичную форму  в виде суммы всевозможных слагаемых в виде суммы всевозможных слагаемых  , где , где 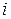 и и  уже независимо друг от друга принимают значения от уже независимо друг от друга принимают значения от 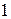 до до  : :
 , (5) , (5)
в частности, при  получается слагаемое получается слагаемое  . .
Из коэффициентов  можно составить, очевидно, квадратную матрицу можно составить, очевидно, квадратную матрицу  порядка порядка  , она называется матрицей квадратичной формы , она называется матрицей квадратичной формы  , а ее ранг , а ее ранг  рангом этой квадратичной формы. Если, в частности, рангом этой квадратичной формы. Если, в частности,  , т.е. матрица – невырожденная, то и квадратичная форма , т.е. матрица – невырожденная, то и квадратичная форма  называется невырожденной. Ввиду равенства (4) элементы матрицы называется невырожденной. Ввиду равенства (4) элементы матрицы  , симметричные относительно главной диагонали, равны между собой, т.е. матрица , симметричные относительно главной диагонали, равны между собой, т.е. матрица  симметрическая. Обратно, для любой симметрической матрицы симметрическая. Обратно, для любой симметрической матрицы   гопорядка можно указать вполне определенную квадратичную форму (5) от гопорядка можно указать вполне определенную квадратичную форму (5) от  неизвестных, имеющую элементы матрицы неизвестных, имеющую элементы матрицы  своими коэффициентами. своими коэффициентами.
УТВЕРЖДЕНИЕ 1. Матрица, полученная транспонированием произведения, равна произведению матриц, получающихся транспонированием сомножителей, притом взятых в обратном порядке,
 (6) (6)
ДОКАЗАТЕЛЬСТВО. Действительно, если произведение 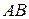 . определено, то будет определено, как легко проверить, и произведение . определено, то будет определено, как легко проверить, и произведение  : число столбцов матрицы : число столбцов матрицы  равно числу строк матрицы равно числу строк матрицы  . Элемент матрицы . Элемент матрицы  , стоящий в ее , стоящий в ее  ой строке и ой строке и  ом столбце, в матрице ом столбце, в матрице 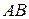 расположен в расположен в  ой строке и ой строке и  ом столбце. Он равен, поэтому, сумме произведений соответственных элементов ом столбце. Он равен, поэтому, сумме произведений соответственных элементов  ой строки матрицы ой строки матрицы  и и  го столбца матрицы го столбца матрицы 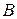 , т.е. равен сумме произведений соответственных элементов , т.е. равен сумме произведений соответственных элементов  го столбца матрицы го столбца матрицы  и и  ой строки матрицы ой строки матрицы  . □ . □
УТВЕРЖДЕНИЕ 2. Матрица  тогда и только тогда будет симметрической, когда она совпадает со своей транспонированной, т.е. тогда и только тогда будет симметрической, когда она совпадает со своей транспонированной, т.е.
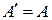 . □ . □
Обозначим теперь через  столбец, составленный из неизвестных, столбец, составленный из неизвестных,
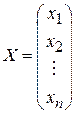 . .
Транспонируя эту матрицу, получим матрицу
 . .
Квадратичная форма (5) с матрицей  может быть записана теперь в виде следующего произведения: может быть записана теперь в виде следующего произведения:
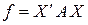 (7) (7)
Действительно, произведение  будет матрицей, состоящей из одного столбца: будет матрицей, состоящей из одного столбца:
 . .
Умножая эту матрицу слева на матрицу  , мы получим «матрицу», состоящую из одной строки и одного столбца, а именно правую часть равенства (5). , мы получим «матрицу», состоящую из одной строки и одного столбца, а именно правую часть равенства (5).
Рассмотрим, далее, линейное преобразование переменных  , входящих в квадратичную форму , входящих в квадратичную форму  . .
 . (8) . (8)
Матрицей этого преобразования будет  . Преобразование называется невырожденным, если матрица . Преобразование называется невырожденным, если матрица  невырожденная. При этом считаем, что если форма невырожденная. При этом считаем, что если форма  действительная, то и элементы матрицы действительная, то и элементы матрицы 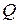 должны быть действительными. должны быть действительными.
Обозначая через  столбец из неизвестных столбец из неизвестных  , запишем линейное преобразование (8) в виде матричного равенства: , запишем линейное преобразование (8) в виде матричного равенства:
 . (9) . (9)
ТЕОРЕМА 1. Квадратичная форма от  неизвестных, имеющая матрицу неизвестных, имеющая матрицу  , после выполнения линейного преобразования неизвестных с матрицей , после выполнения линейного преобразования неизвестных с матрицей 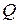 превращается в квадратичную форму от новых неизвестных, причем матрицей этой формы служит произведение превращается в квадратичную форму от новых неизвестных, причем матрицей этой формы служит произведение  . .
ДОКАЗАТЕЛЬСТВО. Так как  , то по (6) имеем: , то по (6) имеем:
 . (10) . (10)
Подставляя (9) и (10) в запись (7) формы  , получаем: , получаем:
 , ,
или
 , ,
где
 . .
Матрица 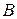 будет симметрической, так как ввиду равенства (6), справедливого, очевидно, для любого числа множителей, и равенства будет симметрической, так как ввиду равенства (6), справедливого, очевидно, для любого числа множителей, и равенства 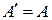 , равносильного симметричности матрицы , равносильного симметричности матрицы  , имеем: , имеем:
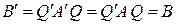 . □ . □
УТВЕРЖДЕНИЕ 3. Ранг квадратичной формы не меняется при выполнении невырожденного линейного преобразования.
ДОКАЗАТЕЛЬСТВО. Докажем вначале, что ранг произведения матриц не выше ранга сомножителей. Действительно, каждая строка произведения двух матриц  и и  является линейной комбинацией строк матрицы является линейной комбинацией строк матрицы  , а поэтому, ранг , а поэтому, ранг  не выше ранга не выше ранга  . Аналогично, столбцы матрицы . Аналогично, столбцы матрицы  являются линейными комбинациями столбцов матрицы являются линейными комбинациями столбцов матрицы  , значит, ранг , значит, ранг  не выше ранга не выше ранга  . .
Пусть теперь  , где , где  невырожденная матрица, тогда ранг невырожденная матрица, тогда ранг 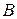 не выше ранга не выше ранга  . Аналогично, . Аналогично,  , следовательно, ранг , следовательно, ранг  не выше ранга не выше ранга 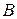 . □ . □
Рассмотрим теперь, по аналогии с указанной в начале параграфа геометрической задачей, вопрос о приведении произвольной квадратичной формы некоторым невырожденным линейным преобразованием к виду
 . (11) . (11)
Этот специальный вид квадратичной формы называется каноническим.
УТВЕРЖДЕНИЕ 4. Число отличных от нуля коэффициентов в (11) равно рангу  формы формы  . .
ДОКАЗАТЕЛЬСТВО. Пусть квадратичная форма  от от  неизвестных неизвестных  уже приведена невырожденным линейным преобразованием к каноническому виду (11), где уже приведена невырожденным линейным преобразованием к каноническому виду (11), где  новые неизвестные. Некоторые из коэффициентов новые неизвестные. Некоторые из коэффициентов  могут, конечно, быть нулями. Матрица этой квадратичной формы имеет диагональный вид могут, конечно, быть нулями. Матрица этой квадратичной формы имеет диагональный вид
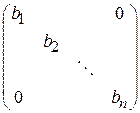 . .
По предложению 3 эта матрица имеет ранг  , что равносильно утверждению, что на ее главной диагонали стоит ровно , что равносильно утверждению, что на ее главной диагонали стоит ровно  отличных от нуля элементов. □ отличных от нуля элементов. □
ТЕОРЕМА 2. (основная о квадратичных формах). Всякая квадратичная форма может быть приведена некоторым невырожденным линейным преобразованием к каноническому виду. Если при этом рассматривается действительная квадратичная форма, то все коэффициенты указанного линейного преобразования можно считать действительными.
ДОКАЗАТЕЛЬСТВО. Эта теорема верна для случая квадратичных форм от одного неизвестного, так как всякая такая форма имеет вид  , являющийся каноническим. Будем вести доказательство индукцией по числу неизвестных, т. е. доказывать теорему для квадратичных форм от , являющийся каноническим. Будем вести доказательство индукцией по числу неизвестных, т. е. доказывать теорему для квадратичных форм от  неизвестных, считая ее уже доказанной для форм с меньшим числом неизвестных. неизвестных, считая ее уже доказанной для форм с меньшим числом неизвестных.
Пусть дана квадратичная форма
 (12) (12)
от  неизвестных неизвестных  . Мы постараемся найти такое невырожденное линейное преобразование, которое выделило бы из . Мы постараемся найти такое невырожденное линейное преобразование, которое выделило бы из  квадрат одного из неизвестных, т. е. привело бы квадрат одного из неизвестных, т. е. привело бы  к виду суммы этого квадрата и некоторой квадратичной формы от остальных неизвестных. Эта цель легко достигается в том случае, если средикоэффициентов к виду суммы этого квадрата и некоторой квадратичной формы от остальных неизвестных. Эта цель легко достигается в том случае, если средикоэффициентов  , стоящих в матрице формы , стоящих в матрице формы  на главной диагонали, есть отличные от нуля, т. е. если в (12) входит с отличным от нуля коэффициентом квадрат хотя бы одного из неизвестных на главной диагонали, есть отличные от нуля, т. е. если в (12) входит с отличным от нуля коэффициентом квадрат хотя бы одного из неизвестных 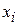 . .
Пусть, например,  . Тогда, как легко проверить, выражение . Тогда, как легко проверить, выражение  , являющееся квадратичной формой, содержит такие же члены с неизвестным , являющееся квадратичной формой, содержит такие же члены с неизвестным  , как и наша форма , как и наша форма  , а поэтому разность , а поэтому разность

будет квадратичной формой, содержащей лишь неизвестные  , но не , но не  . Отсюда . Отсюда

Если введем обозначения
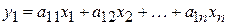 , ,  при при 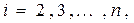 (13) (13)
то получим
 , (14) , (14)
где  будет теперь квадратичной формой от неизвестных будет теперь квадратичной формой от неизвестных 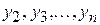 . Выражение (14) есть искомое выражение для формы . Выражение (14) есть искомое выражение для формы  , так как оно получено из (12) невырожденным линейным преобразованием, а именно преобразованием, обратным линейному преобразованию (13), которое имеет своим определителем , так как оно получено из (12) невырожденным линейным преобразованием, а именно преобразованием, обратным линейному преобразованию (13), которое имеет своим определителем  и поэтому не вырождено. и поэтому не вырождено.
Если же имеют место равенства 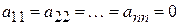 , то предварительно нужно совершить вспомогательное линейное преобразование, приводящее к появлению в нашей форме , то предварительно нужно совершить вспомогательное линейное преобразование, приводящее к появлению в нашей форме  квадратов неизвестных. Так как среди коэффициентов в записи (12) этой формы должны быть отличные от нуля, иначе нечего было бы доказывать, то пусть, например, квадратов неизвестных. Так как среди коэффициентов в записи (12) этой формы должны быть отличные от нуля, иначе нечего было бы доказывать, то пусть, например,  , т. е. , т. е.  является суммой слагаемого является суммой слагаемого  и слагаемых, в каждый из которых входит хотя бы одно из неизвестных и слагаемых, в каждый из которых входит хотя бы одно из неизвестных  . .
Совершим теперь линейное преобразование
 , ,  , ,  при при  . (15) . (15)
Оно будет невырожденным, так как имеет определитель
 . .
В результате этого преобразования слагаемое  нашей формы примет вид нашей формы примет вид
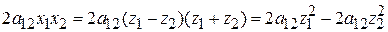 , ,
т. е. в форме  появятся, с отличными от нуля коэффициентами, квадраты сразу двух неизвестных,причемони не могут сократиться ни с одним из остальных членов, так как в каждый из этих последних входит хотя бы одно из неизвестных появятся, с отличными от нуля коэффициентами, квадраты сразу двух неизвестных,причемони не могут сократиться ни с одним из остальных членов, так как в каждый из этих последних входит хотя бы одно из неизвестных  . .
Теперь мы находимся в условиях уже рассмотренного выше случая,
т. е. еще одним невырожденным линейным преобразованием можем привести форму  к виду (14). к виду (14).
Для окончания доказательства остается отметить, что квадратичная форма  зависит от меньшего, чем зависит от меньшего, чем  , числа неизвестных и поэтому, по предположению индукции, некоторым невырожденным преобразованием неизвестных , числа неизвестных и поэтому, по предположению индукции, некоторым невырожденным преобразованием неизвестных 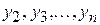 приводится к каноническому виду. Это преобразование, рассматриваемое как (невырожденное, как легко видеть) преобразование всех приводится к каноническому виду. Это преобразование, рассматриваемое как (невырожденное, как легко видеть) преобразование всех  неизвестных, при котором неизвестных, при котором  остается без изменения, приводит, следовательно, (14) к каноническому виду. Таким образом, квадратичная форма остается без изменения, приводит, следовательно, (14) к каноническому виду. Таким образом, квадратичная форма  двумя или тремя невырожденными линейными преобразованиями, которые можно заменить одним невырожденным преобразованием двумя или тремя невырожденными линейными преобразованиями, которые можно заменить одним невырожденным преобразованием  их произведением, приводится к виду суммы квадратов неизвестных с некоторыми коэффициентами. Число этих квадратов равно, как мы знаем, рангу формы их произведением, приводится к виду суммы квадратов неизвестных с некоторыми коэффициентами. Число этих квадратов равно, как мы знаем, рангу формы  . Если, сверх того, квадратичная форма . Если, сверх того, квадратичная форма  действительная, то коэффициенты как в каноническом виде формы действительная, то коэффициенты как в каноническом виде формы  , так в линейном преобразовании, приводящем , так в линейном преобразовании, приводящем  к этому виду, будут действительными; в самом деле, и линейное преобразование, обратное (13), и линейное преобразование (15) имеют действительные коэффициенты. □ к этому виду, будут действительными; в самом деле, и линейное преобразование, обратное (13), и линейное преобразование (15) имеют действительные коэффициенты. □
Метод, использованный в этом доказательстве, может быть применен в конкретных примерах для действительного приведения квадратичной формы к каноническому виду. Нужно лишь вместо индукции, которую мы использовали в доказательстве, последовательно выделять изложенным выше методом квадраты неизвестных.
Пример 1. Привести к каноническому виду квадратичную форму
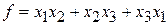
Решение. Ввиду отсутствия в этой форме квадратов неизвестных мы выполним сначала невырожденное линейное преобразование
 , ,  , , 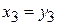
с матрицей
 , ,
после чего получим:
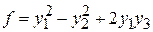 . .
Теперь коэффициент при  отличен от нуля, и поэтому из нашей формы можно выделить квадрат одного неизвестного. Полагая отличен от нуля, и поэтому из нашей формы можно выделить квадрат одного неизвестного. Полагая
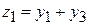 , ,  , , 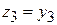 , ,
т. е. совершая линейное преобразование, для которого обратное будет иметь матрицу
 , ,
мы приведем  к каноническому виду к каноническому виду
 . .
Линейное преобразование, приводящее исходную квадратичную форму к каноническому виду, будет иметь своей матрицей произведение
 . .
Можно и непосредственной подстановкой проверить, что невырожденное (так как определитель равен  ) линейное преобразование ) линейное преобразование
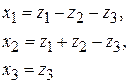
превращает исходную квадратичную форму к каноническому виду.
|



 . (1)
. (1) (величина которого зависит от коэффициентов
(величина которого зависит от коэффициентов  ), т.е. такой переход от координат
), т.е. такой переход от координат  к координатам
к координатам  :
: (2)
(2) , (3)
, (3) равен, следовательно, нулю. Преобразование координат (2) можно толковать, очевидно, как линейное преобразование неизвестных, притом невырожденное, так как определитель из его коэффициентов равен единице. Это преобразование применяется к левой части уравнения (1), и поэтому можно сказать, что левая часть уравнения (1) невырожденным линейным преобразованием (2) превращается в левую часть уравнения (3).
равен, следовательно, нулю. Преобразование координат (2) можно толковать, очевидно, как линейное преобразование неизвестных, притом невырожденное, так как определитель из его коэффициентов равен единице. Это преобразование применяется к левой части уравнения (1), и поэтому можно сказать, что левая часть уравнения (1) невырожденным линейным преобразованием (2) превращается в левую часть уравнения (3). , а коэффициенты являются или действительными, или же любыми комплексными числами.
, а коэффициенты являются или действительными, или же любыми комплексными числами. от
от  называется сумма, каждое слагаемое которой является или квадратом одного из этих неизвестных, или произведением двух разных неизвестных. Квадратичная форма называется действительной или комплексной в зависимости от того, являются ли ее коэффициенты действительными или же могут быль любыми комплексными числами.
называется сумма, каждое слагаемое которой является или квадратом одного из этих неизвестных, или произведением двух разных неизвестных. Квадратичная форма называется действительной или комплексной в зависимости от того, являются ли ее коэффициенты действительными или же могут быль любыми комплексными числами.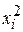 обозначим через
обозначим через  , а коэффициент при произведении
, а коэффициент при произведении  для
для  через
через  . Так как, однако,
. Так как, однако,  , то коэффициент при этом произведении мог бы быть обозначен и через
, то коэффициент при этом произведении мог бы быть обозначен и через  , т.е. введенные нами обозначения предполагают справедливость равенства
, т.е. введенные нами обозначения предполагают справедливость равенства . (4)
. (4) можно записать теперь в виде
можно записать теперь в виде 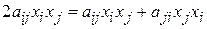 , а всю квадратичную форму
, а всю квадратичную форму  в виде суммы всевозможных слагаемых
в виде суммы всевозможных слагаемых  , где
, где 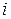 и
и  уже независимо друг от друга принимают значения от
уже независимо друг от друга принимают значения от 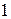 до
до  , (5)
, (5) получается слагаемое
получается слагаемое  .
. можно составить, очевидно, квадратную матрицу
можно составить, очевидно, квадратную матрицу  порядка
порядка  рангом этой квадратичной формы. Если, в частности,
рангом этой квадратичной формы. Если, в частности,  , т.е. матрица – невырожденная, то и квадратичная форма
, т.е. матрица – невырожденная, то и квадратичная форма  , симметричные относительно главной диагонали, равны между собой, т.е. матрица
, симметричные относительно главной диагонали, равны между собой, т.е. матрица  симметрическая. Обратно, для любой симметрической матрицы
симметрическая. Обратно, для любой симметрической матрицы  гопорядка можно указать вполне определенную квадратичную форму (5) от
гопорядка можно указать вполне определенную квадратичную форму (5) от  (6)
(6)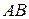 . определено, то будет определено, как легко проверить, и произведение
. определено, то будет определено, как легко проверить, и произведение  : число столбцов матрицы
: число столбцов матрицы  равно числу строк матрицы
равно числу строк матрицы  . Элемент матрицы
. Элемент матрицы  , стоящий в ее
, стоящий в ее  ой строке и
ой строке и  ом столбце, в матрице
ом столбце, в матрице  , т.е. равен сумме произведений соответственных элементов
, т.е. равен сумме произведений соответственных элементов 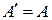 . □
. □ столбец, составленный из неизвестных,
столбец, составленный из неизвестных,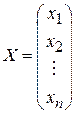 .
. .
. может быть записана теперь в виде следующего произведения:
может быть записана теперь в виде следующего произведения: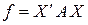 (7)
(7) будет матрицей, состоящей из одного столбца:
будет матрицей, состоящей из одного столбца: .
. , мы получим «матрицу», состоящую из одной строки и одного столбца, а именно правую часть равенства (5).
, мы получим «матрицу», состоящую из одной строки и одного столбца, а именно правую часть равенства (5). , входящих в квадратичную форму
, входящих в квадратичную форму  . (8)
. (8) . Преобразование называется невырожденным, если матрица
. Преобразование называется невырожденным, если матрица  невырожденная. При этом считаем, что если форма
невырожденная. При этом считаем, что если форма 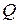 должны быть действительными.
должны быть действительными. столбец из неизвестных
столбец из неизвестных  , запишем линейное преобразование (8) в виде матричного равенства:
, запишем линейное преобразование (8) в виде матричного равенства: . (9)
. (9) .
. . (10)
. (10) ,
, ,
, .
.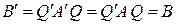 . □
. □ не выше ранга
не выше ранга  , следовательно, ранг
, следовательно, ранг  . (11)
. (11) формы
формы  новые неизвестные. Некоторые из коэффициентов
новые неизвестные. Некоторые из коэффициентов  могут, конечно, быть нулями. Матрица этой квадратичной формы имеет диагональный вид
могут, конечно, быть нулями. Матрица этой квадратичной формы имеет диагональный вид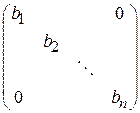 .
. , являющийся каноническим. Будем вести доказательство индукцией по числу неизвестных, т. е. доказывать теорему для квадратичных форм от
, являющийся каноническим. Будем вести доказательство индукцией по числу неизвестных, т. е. доказывать теорему для квадратичных форм от  , стоящих в матрице формы
, стоящих в матрице формы 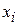 .
. . Тогда, как легко проверить, выражение
. Тогда, как легко проверить, выражение  , являющееся квадратичной формой, содержит такие же члены с неизвестным
, являющееся квадратичной формой, содержит такие же члены с неизвестным  , как и наша форма
, как и наша форма 
 , но не
, но не 
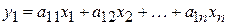 ,
,  при
при 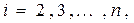 (13)
(13) , (14)
, (14) будет теперь квадратичной формой от неизвестных
будет теперь квадратичной формой от неизвестных 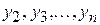 . Выражение (14) есть искомое выражение для формы
. Выражение (14) есть искомое выражение для формы  и поэтому не вырождено.
и поэтому не вырождено.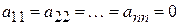 , то предварительно нужно совершить вспомогательное линейное преобразование, приводящее к появлению в нашей форме
, то предварительно нужно совершить вспомогательное линейное преобразование, приводящее к появлению в нашей форме  , т. е.
, т. е.  и слагаемых, в каждый из которых входит хотя бы одно из неизвестных
и слагаемых, в каждый из которых входит хотя бы одно из неизвестных  .
. ,
,  ,
,  при
при  . (15)
. (15) .
.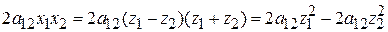 ,
, .
. остается без изменения, приводит, следовательно, (14) к каноническому виду. Таким образом, квадратичная форма
остается без изменения, приводит, следовательно, (14) к каноническому виду. Таким образом, квадратичная форма  их произведением, приводится к виду суммы квадратов неизвестных с некоторыми коэффициентами. Число этих квадратов равно, как мы знаем, рангу формы
их произведением, приводится к виду суммы квадратов неизвестных с некоторыми коэффициентами. Число этих квадратов равно, как мы знаем, рангу формы 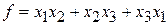
 ,
,  ,
, 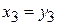
 ,
,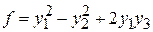 .
. отличен от нуля, и поэтому из нашей формы можно выделить квадрат одного неизвестного. Полагая
отличен от нуля, и поэтому из нашей формы можно выделить квадрат одного неизвестного. Полагая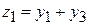 ,
,  ,
, 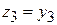 ,
, ,
, .
. .
. ) линейное преобразование
) линейное преобразование