
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приведение квадратичных форм к каноническому видуСодержание книги
Поиск на нашем сайте
Рассмотрим некоторое линейное преобразование А с матрицей Это симметрическое преобразование можно записать в виде: y1 = a11x1 + a12x2 y2 = a12x1 + a22x2 где у1 и у2 – координаты вектора Очевидно, что квадратичная форма может быть записана в виде Ф(х1, х2) = х1у1 + х2у2.
Как видно, геометрический смысл числового значения квадратичной формы Ф в точке с координатами х1 и х2 – скалярное произведение Если взять другой ортонормированный базис на плоскости, то в нем квадратичная форма Ф будет выглядеть иначе, хотя ее числовое значение в каждой геометрической точке и не изменится. Если найти такой базис, в котором квадратичная форма не будет содержать координат в первой степени, а только координаты в квадрате, то квадратичную форму можно будет привести к каноническому виду. Если в качестве базиса взять совокупность собственных векторов линейного преобразования, то в этом базисе матрица линейного преобразования имеет вид:
При переходе к новому базису от переменных х1 и х2 мы переходим к переменным
Тогда
Теория квадратичных форм используется для приведения к каноническому виду уравнений кривых и поверхностей второго порядка.
Пример. Привести к каноническому виду квадратичную форму Ф(х1, х2) = 27
Коэффициенты: а11 = 27, а12 = 5, а22 = 3. Составим характеристическое уравнение: (27 - l)(3 - l) – 25 = 0 l2 - 30l + 56 = 0 l1 = 2; l2 = 28;
Пример. Привести к каноническому виду уравнение второго порядка: 17x2 + 12xy + 8y2 – 20 = 0.
Коэффициенты а11 = 17, а12 = 6, а22 = 8. А = Составим характеристическое уравнение: (17 - l)(8 - l) - 36 = 0 136 - 8l - 17l + l2 – 36 = 0 l2 - 25l + 100 = 0 l1 = 5, l2 = 20. Итого:
Пример. Используя теорию квадратичных форм, привести к каноническому виду уравнение линии второго порядка. Схематично изобразить график.
Решение: Составим характеристическое уравнение квадратичной формы
Решив это уравнение, получим l1 = 2, l2 = 6. Найдем координаты собственных векторов:
Собственные векторы:
Находим координаты единичных векторов нового базиса.
Имеем следующее уравнение линии в новой системе координат:
Каноническое уравнение линии в новой системе координат будет иметь вид:
Пример. Используя теорию квадратичных форм, привести к каноническому виду уравнение линии второго порядка. Схематично изобразить график.
Решение: Составим характеристическое уравнение квадратичной формы
Решив это уравнение, получим l1 = 1, l2 = 11. Найдем координаты собственных векторов:
Собственные векторы:
Находим координаты единичных векторов нового базиса.
Имеем следующее уравнение линии в новой системе координат:
Каноническое уравнение линии в новой системе координат будет иметь вид:
Пример. Используя теорию квадратичных форм, привести к каноническому виду уравнение линии второго порядка. Схематично изобразить график. 4ху + 3у2 + 16 = 0
Коэффициенты: a11 = 0; a12 = 2; a22 = 3. Характеристическое уравнение: Корни: l1 = -1, l2 = 4.
Для l1 = -1 Для l2 = 4
m1 = 1; n1 = -0,5; m2 = 1; n2 = 2;
Получаем:
|
||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 237; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.008 с.) |

 .
. в базисе
в базисе  .
. .
. .
. и
и  . Тогда:
. Тогда:
 .
. Выражение
Выражение  называется каноническим видом квадратичной формы. Аналогично можно привести к каноническому виду квадратичную форму с большим числом переменных.
называется каноническим видом квадратичной формы. Аналогично можно привести к каноническому виду квадратичную форму с большим числом переменных. .
. ;
;


 - каноническое уравнение эллипса.
- каноническое уравнение эллипса.
 : при
: при 

 полагая m1 = 1, получим n1 =
полагая m1 = 1, получим n1 = 
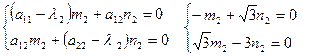 полагая m2 = 1, получим n2 =
полагая m2 = 1, получим n2 = 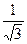

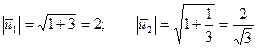





 : при
: при 

 полагая m1 = 1, получим n1 =
полагая m1 = 1, получим n1 = 
 полагая m2 = 1, получим n2 =
полагая m2 = 1, получим n2 = 
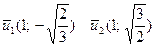







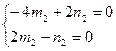
 = (1; -0,5)
= (1; -0,5)  = (1; 2)
= (1; 2)



 -каноническое уравнение гиперболы.
-каноническое уравнение гиперболы.



