Глава III. Жорданова нормальная форма матрицы.
§3.1.  матрицы, их эквивалентность. матрицы, их эквивалентность.
В этой главе займёмся изучением квадратных матриц порядка  , элементами которых служат многочлены произвольных степеней от одного неизвестного , элементами которых служат многочлены произвольных степеней от одного неизвестного 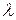 с коэффициентами из поля с коэффициентами из поля 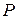 . Такие матрицы называются многочленными матрицами или полиномиальными матрицами, или, короче, . Такие матрицы называются многочленными матрицами или полиномиальными матрицами, или, короче,  матрицами. Примером матрицами. Примером  матрицы может служить характеристическая матрица матрицы может служить характеристическая матрица  произвольной квадратной матрицы произвольной квадратной матрицы  с элементами из поля с элементами из поля 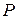 ; на главной диагонали этой матрицы стоят многочлены первой степени, вне главной диагонали ; на главной диагонали этой матрицы стоят многочлены первой степени, вне главной диагонали  многочлены нулевой степени или нули. Всякая матрица с элементами из поля многочлены нулевой степени или нули. Всякая матрица с элементами из поля 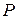 также будет частным случаем также будет частным случаем  матрицы. Такие матрицы для краткости будем называть числовыми матрицами, ее элементы являются многочленами нулевой степени или нулями. В общем случае матрицы. Такие матрицы для краткости будем называть числовыми матрицами, ее элементы являются многочленами нулевой степени или нулями. В общем случае  матрица выглядит следующим образом: матрица выглядит следующим образом:
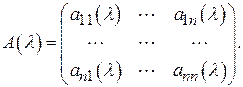
Назовем элементарными преобразованиями этой матрицы преобразования следующих двух типов:
1) умножение любой строки (столбца) матрицы  на любое число на любое число  из поля из поля 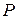 , отличное от нуля; , отличное от нуля;
2) прибавление к любой  ой строке ( ой строке ( ому столбцу) матрицы ому столбцу) матрицы  любой её любой её  ой строки ( ой строки ( ого столбца), ого столбца),  , притом умноженной (умноженного) на любой многочлен , притом умноженной (умноженного) на любой многочлен  из кольца из кольца 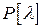 . .
Легко видеть, что для каждого из элементарных преобразований  матрицы существует обратное преобразование, также являющееся элементарным. Так, обратным для преобразования 1) будет элементарное преобразование, состоящее в умножении той же строки (столбца) на число матрицы существует обратное преобразование, также являющееся элементарным. Так, обратным для преобразования 1) будет элементарное преобразование, состоящее в умножении той же строки (столбца) на число  , существующее ввиду условия , существующее ввиду условия  ; а обратным для преобразования 2) будет преобразование, состоящее в прибавлении к ; а обратным для преобразования 2) будет преобразование, состоящее в прибавлении к  ой строке ( ой строке ( ому столбцу) ому столбцу)  ой строки ( ой строки ( ого столбца), умноженной (умноженного) на ого столбца), умноженной (умноженного) на  . .
УТВЕРЖДЕНИЕ 1. В матрице  можно при помощи нескольких элементарных преобразований переставить любые две строки или любые два столбца. можно при помощи нескольких элементарных преобразований переставить любые две строки или любые два столбца.
ДОКАЗАТЕЛЬСТВО. Пусть, например, нужно переставить  ую и ую и  ую строки матрицы ую строки матрицы  . Это можно сделать при помощи четырех элементарных преобразований, как показывает следующая схема: . Это можно сделать при помощи четырех элементарных преобразований, как показывает следующая схема:

Здесь последовательно были выполнены следующие преобразования
a) к  ой строке прибавлена ой строке прибавлена  ая; b) из ая; b) из  ой строки вычтена новая ой строки вычтена новая  ая; c) к новой ая; c) к новой  ой строке прибавлена новая ой строке прибавлена новая  ая; d) новая ая; d) новая  ая строка умножена на ая строка умножена на  . □ . □
Будем говорить, что  матрицы матрицы  и и  эквивалентны, и записывать эквивалентны, и записывать  , если от матрицы , если от матрицы  можно перейти к матрице можно перейти к матрице  при помощи конечного числа элементарных преобразований. Отношение при помощи конечного числа элементарных преобразований. Отношение  является, очевидно, рефлексивным и транзитивным, а также и симметричным ввиду существования для каждого элементарного преобразования обратного элементарного преобразования, т. е. является отношением эквивалентности. Таким образом, все квадратные является, очевидно, рефлексивным и транзитивным, а также и симметричным ввиду существования для каждого элементарного преобразования обратного элементарного преобразования, т. е. является отношением эквивалентности. Таким образом, все квадратные  матрицы порядка матрицы порядка  над полем над полем 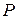 распадаются на непересекающиеся классы эквивалентных матриц. Нашей ближайшей целью является разыскание среди всех распадаются на непересекающиеся классы эквивалентных матриц. Нашей ближайшей целью является разыскание среди всех  матриц, эквивалентных данной матрице матриц, эквивалентных данной матрице  , наиболее простого представителя класса эквивалентности. Для этого введем следующее понятие. Канонической , наиболее простого представителя класса эквивалентности. Для этого введем следующее понятие. Канонической  матрицей называется матрицей называется  матрица, обладающая следующими тремя свойствами: матрица, обладающая следующими тремя свойствами:
а) эта матрица диагональная, т. е. имеет вид
 ; (1) ; (1)
б) всякий многочлен  , нацело делится на многочлен , нацело делится на многочлен  ; ;
в) старший коэффициент каждого многочлена  , равен единице, если этот многочлен отличен от нуля. , равен единице, если этот многочлен отличен от нуля.
Отметим, что если среди многочленов 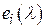 , стоящих на главной диагонали канонической , стоящих на главной диагонали канонической  матрицы (1),встречаются равные нулю, то, ввиду свойства б), они непременно занимают на главной диагонали последние места. С другой стороны, если среди многочленов матрицы (1),встречаются равные нулю, то, ввиду свойства б), они непременно занимают на главной диагонали последние места. С другой стороны, если среди многочленов 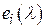 встречаются многочлены нулевой степени, то, по свойству в), все они равны встречаются многочлены нулевой степени, то, по свойству в), все они равны 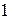 и, по свойству б), занимают на главной диагонали матрицы (1) первые места. и, по свойству б), занимают на главной диагонали матрицы (1) первые места.
К числу канонических  матриц принадлежат, в частности, некоторые числовые матрицы, в том числе матрицы единичная и нулевая. матриц принадлежат, в частности, некоторые числовые матрицы, в том числе матрицы единичная и нулевая.
ТЕОРЕМА 1. (о канонической  матрице). Всякую матрице). Всякую  матрицу с помощью элементарных преобразований можно привести к каноническому виду. матрицу с помощью элементарных преобразований можно привести к каноническому виду.
ДОКАЗАТЕЛЬСТВО. Будем доказывать теорему индукцией по порядку  рассматриваемых рассматриваемых  матриц. Действительно, при матриц. Действительно, при  будет будет
 . .
Если  то матрица уже каноническая. Если же то матрица уже каноническая. Если же  , то достаточно умножить многочлен , то достаточно умножить многочлен 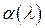 на элемент, обратный для его старшего коэффициента, (а это будет элементарное преобразование матрицы) получим канонический вид. на элемент, обратный для его старшего коэффициента, (а это будет элементарное преобразование матрицы) получим канонический вид.
Пусть теорема уже доказана для  матриц порядка матриц порядка  . Рассмотрим произвольную . Рассмотрим произвольную  матрицу матрицу  порядка порядка  . Если она нулевая, то уже является канонической. Будем считать, что среди элементов матрицы . Если она нулевая, то уже является канонической. Будем считать, что среди элементов матрицы  имеются ненулевые. имеются ненулевые.
Переставляя, если понадобится, строки и столбцы матрицы  можно добиться того, чтобы один из ненулевых элементов располагался в левом верхнем углу. Рассмотрим все такие матрицы. Многочлены, стоящие в левом верхнем углу этих матриц, могут иметь разные степени. Степень многочлена является натуральным числом, значит можно найти среди всех можно добиться того, чтобы один из ненулевых элементов располагался в левом верхнем углу. Рассмотрим все такие матрицы. Многочлены, стоящие в левом верхнем углу этих матриц, могут иметь разные степени. Степень многочлена является натуральным числом, значит можно найти среди всех  матриц, эквивалентных матрице матриц, эквивалентных матрице  и имеющих ненулевой элемент в левом верхнем углу, такую (одну из таких), что многочлен, стоящий в ее левом верхнем углу, имеет наименьшую возможную степень. Деля первую строку этой матрицы на старший коэффициент указанного многочлена, мы получим и имеющих ненулевой элемент в левом верхнем углу, такую (одну из таких), что многочлен, стоящий в ее левом верхнем углу, имеет наименьшую возможную степень. Деля первую строку этой матрицы на старший коэффициент указанного многочлена, мы получим  матрицу, эквивалентную матрице матрицу, эквивалентную матрице  , ,

что  , старший коэффициент этого многочлена равен , старший коэффициент этого многочлена равен 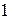 , и невозможно с помощью элементарных преобразований перейти от полученной матрицы к такой матрице, в левом верхнем углу которой стоял бы ненулевой многочлен меньшей степени. , и невозможно с помощью элементарных преобразований перейти от полученной матрицы к такой матрице, в левом верхнем углу которой стоял бы ненулевой многочлен меньшей степени.
Докажем теперь, что все элементы первой строки и первого столбца полученной матрицы нацело делятся на  . Пусть, например, для . Пусть, например, для 
 , ,
где степень  меньше степени меньше степени  , если , если  отлично от нуля. Тогда, вычитая из отлично от нуля. Тогда, вычитая из  ого столбца нашей матрицы ее первый столбец, умноженный на ого столбца нашей матрицы ее первый столбец, умноженный на  , а затем, переставляя первый и , а затем, переставляя первый и  ый столбцы, придем к такой матрице, эквивалентной матрице ый столбцы, придем к такой матрице, эквивалентной матрице  , в левом верхнем углу которой стоит многочлен , в левом верхнем углу которой стоит многочлен  , т. е. многочлен меньшей степени, чем , т. е. многочлен меньшей степени, чем  , что противоречит выбору этого многочлена. Отсюда следует , что противоречит выбору этого многочлена. Отсюда следует  . .
Вычитая теперь из  ого столбца матрицы ее первый столбец, умноженный на ого столбца матрицы ее первый столбец, умноженный на  , заменим элемент , заменим элемент 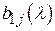 нулем. Делая такие преобразования для нулем. Делая такие преобразования для  , заменим нулями все элементы , заменим нулями все элементы 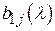 . Аналогично заменяются нулями и все элементы . Аналогично заменяются нулями и все элементы 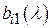 , , 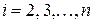 . Таким образом получим матрицу, эквивалентную матрице . Таким образом получим матрицу, эквивалентную матрице  , в левом верхнем углу которой стоит многочлен , в левом верхнем углу которой стоит многочлен  , а все остальные элементы первой строки и первого столбца равны нулю, т. е. , а все остальные элементы первой строки и первого столбца равны нулю, т. е.
 . (2) . (2)
По индуктивному предположению, матрица  ого порядка, стоящая в правом нижнем углу полученной матрицы (2), элементарными преобразованиями приводится к каноническому виду: ого порядка, стоящая в правом нижнем углу полученной матрицы (2), элементарными преобразованиями приводится к каноническому виду:
 . .
Совершив эти же преобразования над соответствующими строками и столбцами матрицы (2)  при этом первая строка и первый столбец этой матрицы останутся, очевидно, без изменения, при этом первая строка и первый столбец этой матрицы останутся, очевидно, без изменения,  мы получим, что, мы получим, что,
 . (3) . (3)
Для доказательства того, что матрица (3) является канонической, покажем, что 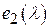 нацело делится на нацело делится на  . Пусть . Пусть
 , ,
где  и степень и степень  меньше степени меньше степени  . Прибавляя ко второму столбцу матрицы (3) ее первый столбец, умноженный на . Прибавляя ко второму столбцу матрицы (3) ее первый столбец, умноженный на  , а затем вычитая из второй строки первую строку, мы заменим элемент , а затем вычитая из второй строки первую строку, мы заменим элемент 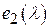 элементом элементом  . Переставляя, далее, первые две строки и первые два столбца, мы переместим многочлен . Переставляя, далее, первые две строки и первые два столбца, мы переместим многочлен  в левый верхний угол матрицы, что противоречит выбору многочлена в левый верхний угол матрицы, что противоречит выбору многочлена  . □ . □
Пусть дана произвольная  матрица матрица  порядка порядка  . Фиксируем некоторое натуральное число . Фиксируем некоторое натуральное число  и рассмотрим все миноры и рассмотрим все миноры  ого порядка матрицы ого порядка матрицы  . Вычисляя эти миноры, получим конечную систему многочленов от . Вычисляя эти миноры, получим конечную систему многочленов от 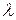 ; наибольший общий делитель этой системы многочленов, взятый со старшим коэффициентом ; наибольший общий делитель этой системы многочленов, взятый со старшим коэффициентом 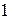 , обозначим через , обозначим через  . .
Получим многочлены
 , (4) , (4)
однозначно определяемые самой матрицей  . .
При этом  есть наибольший общий делитель всех элементов матрицы есть наибольший общий делитель всех элементов матрицы  , взятый с коэффициентом 1, a , взятый с коэффициентом 1, a  равен определителю матрицы равен определителю матрицы  , деленному на его старший коэффициент. , деленному на его старший коэффициент.
Заметим также, что если матрица  имеет ранг имеет ранг  , то , то
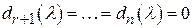 , ,
в то время как все остальные многочлены системы (4) отличны от нуля.
ТЕОРЕМА 2. (о НОДах эквивалентных матриц). Наибольший общий делитель  всех миноров всех миноров  ого порядка ого порядка  матрицы матрицы  , ,  , не меняется при выполнении в матрице , не меняется при выполнении в матрице  элементарных преобразований. элементарных преобразований.
ДОКАЗАТЕЛЬСТВО. Утверждение почти очевидно для того случая, когда в матрице  выполняется элементарное преобразование типа 1). Так, например, если выполняется элементарное преобразование типа 1). Так, например, если  ая строка матрицы умножается на число ая строка матрицы умножается на число  из поля из поля 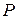 , ,  , то те миноры , то те миноры  ого порядка, через которые ого порядка, через которые  ая строка проходит, будут умножаться на ая строка проходит, будут умножаться на  , все же остальные миноры , все же остальные миноры  ого порядка останутся без изменения. Однако при разыскании наибольшего общего делителя нескольких многочленов любые из этих многочленов можно беспрепятственно умножать на отличные от нуля числа из поля ого порядка останутся без изменения. Однако при разыскании наибольшего общего делителя нескольких многочленов любые из этих многочленов можно беспрепятственно умножать на отличные от нуля числа из поля 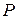 (§4.4 (§4.4  ). ).
Рассмотрим теперь элементарные преобразования типа 2). Пусть, например, к  ой строке, матрицы ой строке, матрицы  прибавляется ее прибавляется ее  ая строка, ая строка,  , умноженная на многочлен , умноженная на многочлен  . Получающуюся после этого преобразования матрицу обозначим через . Получающуюся после этого преобразования матрицу обозначим через  , а наибольший общий делитель всех ее миноров , а наибольший общий делитель всех ее миноров  ого порядка, взятый со старшим коэффициентом ого порядка, взятый со старшим коэффициентом 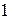 , ,  через через  . Посмотрим, что происходит при указанном преобразовании с минорами . Посмотрим, что происходит при указанном преобразовании с минорами  ого порядка матрицы ого порядка матрицы  . .
Ясно, что не будут меняться те миноры, через которые  ая строка не проходит. Не меняются и те миноры, через которые проходят как ая строка не проходит. Не меняются и те миноры, через которые проходят как  ая, так и ая, так и  ая строки, так как определитель не меняется от прибавления к одной его строке кратного другой его строки. Возьмем, наконец, любой из тех миноров ая строки, так как определитель не меняется от прибавления к одной его строке кратного другой его строки. Возьмем, наконец, любой из тех миноров  ого порядка, через которые проходит ого порядка, через которые проходит  ая строка, но не проходит ая строка, но не проходит  ая; обозначим его через ая; обозначим его через  . Соответствующий минор матрицы . Соответствующий минор матрицы  можно представить, очевидно, как сумму минора можно представить, очевидно, как сумму минора  и умноженного на и умноженного на  минора минора  матрицы матрицы  , получающегося из минора , получающегося из минора  заменой элементов заменой элементов  ой строки матрицы ой строки матрицы  соответствующими элементами ее соответствующими элементами ее  ой строки. Так как и ой строки. Так как и  , и , и  делятся на делятся на  , то и , то и  будет делиться на будет делиться на  . .
Отсюда следует, что все миноры  ого порядка матрицы ого порядка матрицы  нацело делятся на нацело делятся на  , а поэтому и , а поэтому и  делится на делится на  .Так как, однако, для рассматриваемого элементарного преобразования существует обратное элементарное преобразование того же типа, то и .Так как, однако, для рассматриваемого элементарного преобразования существует обратное элементарное преобразование того же типа, то и  делится на делится на  . Если же учесть, что старшие коэффициенты обоих этих многочленов равны . Если же учесть, что старшие коэффициенты обоих этих многочленов равны 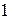 , то , то  . □ . □
СЛЕДСТВИЕ. Всем  матрицам, эквивалентным матрице матрицам, эквивалентным матрице  , соответствует один и тот же набор многочленов (4). □ , соответствует один и тот же набор многочленов (4). □
Это относится, в частности, к любой (если их несколько) канонической матрице, эквивалентной  . Пусть (3) будет одна из таких матриц. . Пусть (3) будет одна из таких матриц.
Вычислим многочлен  , ,  , пользуясь матрицей (3). Ясно, что минор , пользуясь матрицей (3). Ясно, что минор  ого порядка, стоящий в левом верхнем углу этой матрицы, равен произведению ого порядка, стоящий в левом верхнем углу этой матрицы, равен произведению
 (5) (5)
Если, далее, берем в матрице (3) минор  ого порядка, стоящий в строках с номерами ого порядка, стоящий в строках с номерами  , где , где  , и в столбцах с теми же самыми номерами, то этот минор равен произведению , и в столбцах с теми же самыми номерами, то этот минор равен произведению  , которое делится на (5), т. к. , которое делится на (5), т. к. 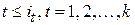 и поэтому и поэтому  делится на делится на  . Наконец, если в матрице (3) взят минор . Наконец, если в матрице (3) взят минор  ого порядка, через который хотя бы для одного ого порядка, через который хотя бы для одного 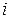 проходит проходит  ая строка этой матрицы, но не проходит ее ая строка этой матрицы, но не проходит ее  ый столбец, то этот минор содержит нулевую строку и поэтому равен нулю. ый столбец, то этот минор содержит нулевую строку и поэтому равен нулю.
Из сказанного следует, что произведение (5) и будет наибольшим общим делителей всех миноров k-го порядка матрицы (3), а поэтому и исходной матрицы  , т. е. , т. е.
 . (6) . (6)
ТЕОРЕМА 3. Всякая  матрица эквивалентна лишь одной канонической матрице. матрица эквивалентна лишь одной канонической матрице.
ДОКАЗАТЕЛЬСТВО. Покажем, что многочлены  , ,  , однозначным образом определяются самой матрицей , однозначным образом определяются самой матрицей  . Пусть ранг этой матрицы равен . Пусть ранг этой матрицы равен  . Тогда, как известно, . Тогда, как известно,  , но , но  , а поэтому, ввиду (6), , а поэтому, ввиду (6),  . Отсюда, ввиду свойств канонической матрицы, вообще следует, что если ранг . Отсюда, ввиду свойств канонической матрицы, вообще следует, что если ранг  матрицы матрицы  меньше меньше  , то , то
 . (7) . (7)
А для  из (6) следует, ввиду из (6) следует, ввиду  , что , что
 . □ (8) . □ (8)
Тем самым мы получили способ непосредственного разыскания многочленов  , называемых инвариантными множителями матрицы , называемых инвариантными множителями матрицы  . .
Анализируя вышесказанное, можем сформулировать основной результат данного параграфа.
ТЕОРЕМА 4. (первый критерий эквивалентности  матриц). Две матриц). Две  матрицы эквивалентны тогда и только тогда, когда они приводятся к одному и тому же каноническому виду. □ матрицы эквивалентны тогда и только тогда, когда они приводятся к одному и тому же каноническому виду. □
Пример 1. Привести к каноническому виду  матрицу матрицу
 . .
Решение. Выполняя цепочку элементарных преобразований, получаем;
 . .
С другой стороны, можно вычислить инвариантные множители матрицы  . Именно, вычисляя наибольший общий делитель элементов этой матрицы, получаем: . Именно, вычисляя наибольший общий делитель элементов этой матрицы, получаем:
 . .
Вычисляя же определитель матрицы  и замечая, что его старший коэффициент равен и замечая, что его старший коэффициент равен 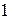 , получаем: , получаем:
 . .
а поэтому
 . .
§3.2. Унимодулярные 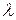 -матрицы. -матрицы.
|



 матрицы, их эквивалентность.
матрицы, их эквивалентность. , элементами которых служат многочлены произвольных степеней от одного неизвестного
, элементами которых служат многочлены произвольных степеней от одного неизвестного 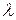 с коэффициентами из поля
с коэффициентами из поля 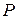 . Такие матрицы называются многочленными матрицами или полиномиальными матрицами, или, короче,
. Такие матрицы называются многочленными матрицами или полиномиальными матрицами, или, короче,  произвольной квадратной матрицы
произвольной квадратной матрицы  с элементами из поля
с элементами из поля  многочлены нулевой степени или нули. Всякая матрица с элементами из поля
многочлены нулевой степени или нули. Всякая матрица с элементами из поля 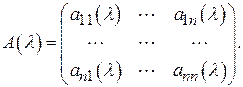
 на любое число
на любое число  из поля
из поля  ой строке (
ой строке ( ой строки (
ой строки ( , притом умноженной (умноженного) на любой многочлен
, притом умноженной (умноженного) на любой многочлен  из кольца
из кольца 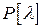 .
. , существующее ввиду условия
, существующее ввиду условия  ; а обратным для преобразования 2) будет преобразование, состоящее в прибавлении к
; а обратным для преобразования 2) будет преобразование, состоящее в прибавлении к  .
.
 . □
. □ эквивалентны, и записывать
эквивалентны, и записывать  , если от матрицы
, если от матрицы  является, очевидно, рефлексивным и транзитивным, а также и симметричным ввиду существования для каждого элементарного преобразования обратного элементарного преобразования, т. е. является отношением эквивалентности. Таким образом, все квадратные
является, очевидно, рефлексивным и транзитивным, а также и симметричным ввиду существования для каждого элементарного преобразования обратного элементарного преобразования, т. е. является отношением эквивалентности. Таким образом, все квадратные  ; (1)
; (1) , нацело делится на многочлен
, нацело делится на многочлен  ;
; , равен единице, если этот многочлен отличен от нуля.
, равен единице, если этот многочлен отличен от нуля.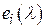 , стоящих на главной диагонали канонической
, стоящих на главной диагонали канонической 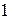 и, по свойству б), занимают на главной диагонали матрицы (1) первые места.
и, по свойству б), занимают на главной диагонали матрицы (1) первые места. будет
будет .
. то матрица уже каноническая. Если же
то матрица уже каноническая. Если же  , то достаточно умножить многочлен
, то достаточно умножить многочлен 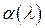 на элемент, обратный для его старшего коэффициента, (а это будет элементарное преобразование матрицы) получим канонический вид.
на элемент, обратный для его старшего коэффициента, (а это будет элементарное преобразование матрицы) получим канонический вид. . Рассмотрим произвольную
. Рассмотрим произвольную  порядка
порядка 
 , старший коэффициент этого многочлена равен
, старший коэффициент этого многочлена равен  . Пусть, например, для
. Пусть, например, для 
 ,
, меньше степени
меньше степени  , а затем, переставляя первый и
, а затем, переставляя первый и  .
.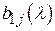 нулем. Делая такие преобразования для
нулем. Делая такие преобразования для  , заменим нулями все элементы
, заменим нулями все элементы 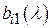 ,
, 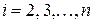 . Таким образом получим матрицу, эквивалентную матрице
. Таким образом получим матрицу, эквивалентную матрице  . (2)
. (2) ого порядка, стоящая в правом нижнем углу полученной матрицы (2), элементарными преобразованиями приводится к каноническому виду:
ого порядка, стоящая в правом нижнем углу полученной матрицы (2), элементарными преобразованиями приводится к каноническому виду: .
. . (3)
. (3)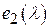 нацело делится на
нацело делится на  ,
, и степень
и степень  и рассмотрим все миноры
и рассмотрим все миноры  ого порядка матрицы
ого порядка матрицы  .
. , (4)
, (4) есть наибольший общий делитель всех элементов матрицы
есть наибольший общий делитель всех элементов матрицы  равен определителю матрицы
равен определителю матрицы  , то
, то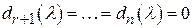 ,
, , не меняется при выполнении в матрице
, не меняется при выполнении в матрице  ).
). , а наибольший общий делитель всех ее миноров
, а наибольший общий делитель всех ее миноров  . Посмотрим, что происходит при указанном преобразовании с минорами
. Посмотрим, что происходит при указанном преобразовании с минорами  . Соответствующий минор матрицы
. Соответствующий минор матрицы  матрицы
матрицы  будет делиться на
будет делиться на  . □
. □ (5)
(5) , где
, где  , и в столбцах с теми же самыми номерами, то этот минор равен произведению
, и в столбцах с теми же самыми номерами, то этот минор равен произведению  , которое делится на (5), т. к.
, которое делится на (5), т. к. 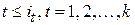 и поэтому
и поэтому  делится на
делится на  . Наконец, если в матрице (3) взят минор
. Наконец, если в матрице (3) взят минор 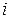 проходит
проходит  . (6)
. (6) ,
,  , но
, но  , а поэтому, ввиду (6),
, а поэтому, ввиду (6),  . Отсюда, ввиду свойств канонической матрицы, вообще следует, что если ранг
. Отсюда, ввиду свойств канонической матрицы, вообще следует, что если ранг  . (7)
. (7) из (6) следует, ввиду
из (6) следует, ввиду  , что
, что . □ (8)
. □ (8) .
. .
. .
. .
. .
.


