
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приведение квадратичной формы к главным осям.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Теория приведения квадратичной формы к каноническому виду, изложенная в предыдущем параграфе, построена по аналогии с геометрической теорией центральных кривых второго порядка, но не может считаться обобщением этой последней теории. В самом деле, в нашей теории допускается использование любых невырожденных линейных преобразований, в то время как приведение кривой второго порядка к каноническому виду достигается применением линейных преобразований весьма специального вида (2), являющихся вращениями плоскости. Эта геометрическая теория может быть, однако, обобщена на случай квадратичных форм от ТЕОРЕМА. Каждая квадратичная форма некоторым ортогональным преобразованием может быть приведена к каноническому виду. ДОКАЗАТЕЛЬСТВО. Будем смотреть на матрицу квадратичной формы как на матрицу некоторого линейного оператора в евклидовом пространстве. Если Но матрица Итак, преобразование неизвестных, имеющее матрицу Тот факт, что матрица линейного оператора Пример 2. Найти ортогональное преобразование, приводящее квадратичную форму
к каноническому виду и написать этот канонический вид. Решение. Матрица этой формы имеет вид
Найдём её характеристический многочлен:
Таким образом, матрица
Найдём ортогональное преобразование, осуществляющее это приведение. Для этого найдём собственные векторы, соответствующие найденным собственным значениям При
Откуда
Применив к ним процесс ортогонализации, получим:
При
Данная система эквивалентна следующей:
решением которой будет
Остаётся нормировать систему
Таким образом искомое преобразование имеет вид:
Для того чтобы найти матрицу преобразования
Закон инерции.
Канонический вид, к которому приводится данная квадратичная форма, определяется неоднозначно. Всякая квадратичная форма может быть приведена к каноническому виду многими различными способами. Возникает вопрос, что общего у тех различных канонических квадратичных форм, к которым приводится данная форма Рассмотрим вначале произвольные комплексные квадратичные формы, допуская употребление невырожденных линейных преобразований также с произвольными комплексными коэффициентами. Известно, что всякая квадратичная форма
где все коэффициенты
Оно приводит форму
называемому нормальным; это Из равенства ТЕОРЕМА 1. Две комплексные квадратичные формы от
Из этой теоремы без труда вытекает СЛЕДСТВИЕ. Каноническим видом комплексной квадратичной формы ранга Иная ситуация в том случае, когда рассматриваются действительные квадратичные формы и допускаются лишь линейные преобразования с действительными коэффициентами. В этом случае уже не всякую форму можно привести к виду (1), так как это могло бы потребовать извлечения квадратного корня из отрицательного числа. Если, однако, мы назовем теперь нормальным видом квадратичной формы сумму квадратов нескольких неизвестных с коэффициентами В самом деле, форма
где все числа
приводит
Общее число входящих сюда квадратов будет равно рангу формы. Действительная квадратичная форма может быть приведена к нормальному виду многими различными преобразованиями, однако с точностью до нумерации неизвестных она приводится лишь к одному нормальному виду. Это показывает следующая: ТЕОРЕМА 2. (закон инерции действительных квадратичных форм). Число положительных и число отрицательных квадратов в нормальном виде, к которому приводится данная квадратичная форма с действительными коэффициентами действительным невырожденным линейным преобразованием, не зависят от выбора этого преобразования. ДОКАЗАТЕЛЬСТВО. Пусть квадратичная форма
Так как переход от неизвестных
Аналогично
причем определители из коэффициентов отличны от нуля. Коэффициенты же как в (3), так и в (4) Предположим теперь, что
Если левые части этих равенств будут заменены их выражениями из (3) и (4), мы получим систему Заменим теперь в равенстве (2) все
Так как все коэффициенты в (3) и (4) действительные, то все квадраты, входящие в равенство (6), положительны, а поэтому (6) влечет за собой равенство нулю всех этих квадратов; отсюда следуют равенства
С другой стороны, по самому выбору чисел
Таким образом, система
с Число положительных квадратов в той нормальной форме, к которой приводится данная действительная квадратичная форма Понятно, что при заданном ранге формы задание любого из определенных сейчас трех чисел вполне определяет два других, и поэтому в дальнейших формулировках можно будет говорить о любом из этих трех чисел. ТЕОРЕМА 3. Две квадратичные формы от ДОКАЗАТЕЛЬСТВО. Действительно, пусть форма
|
||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 2136; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.008 с.) |

 неизвестных с действительными коэффициентами, если потребовать, чтобы матрица преобразования
неизвестных с действительными коэффициентами, если потребовать, чтобы матрица преобразования 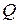 была ортогональной. Такое преобразование называется ортогональным, а сама процедура
была ортогональной. Такое преобразование называется ортогональным, а сама процедура  приведением квадратичных форм к главным осям.
приведением квадратичных форм к главным осям. матрица квадратичной формы, то она симметрическая порядка
матрица квадратичной формы, то она симметрическая порядка  некоторый ортонормированный базис
некоторый ортонормированный базис  мерного евклидова пространства, то матрица
мерного евклидова пространства, то матрица  задаёт в этом базисе симметрический оператор
задаёт в этом базисе симметрический оператор  . По основной теореме о симметрических операторах в евклидовом пространстве в подходящем ортонормированном базисе
. По основной теореме о симметрических операторах в евклидовом пространстве в подходящем ортонормированном базисе  его матрица
его матрица 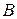 будет диагональной. Пусть
будет диагональной. Пусть  матрица перехода от
матрица перехода от  к
к  .
. . Поэтому
. Поэтому  . А именно так преобразуется матрица
. А именно так преобразуется матрица 
 ,
,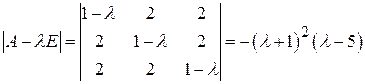 .
. и простой корень
и простой корень  . Следовательно, канонический вид данной квадратичной формы будет
. Следовательно, канонический вид данной квадратичной формы будет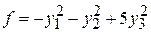 .
. , т. е. решим системы линейных однородных уравнений
, т. е. решим системы линейных однородных уравнений 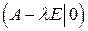 для каждого
для каждого 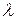 .
. имеем
имеем .
. , т. е. имеются 2 независимые переменные, и фундаментальный набор решений будет:
, т. е. имеются 2 независимые переменные, и фундаментальный набор решений будет:
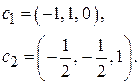
 имеем
имеем .
. ,
,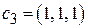 .
. :
:
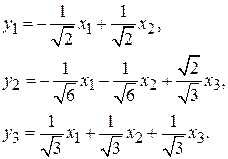

 через
через  , т. е. найти матрицу, обратную матрице преобразования
, т. е. найти матрицу, обратную матрице преобразования  .
. ? Этот вопрос тесно связан с другим вопросом: при каком условии одна из двух данных квадратичных форм может быть переведена в другую невырожденным линейным преобразованием? Ответ на эти вопросы, оказывается, зависит от того, рассматриваются ли комплексные или действительные квадратичные формы.
? Этот вопрос тесно связан с другим вопросом: при каком условии одна из двух данных квадратичных форм может быть переведена в другую невырожденным линейным преобразованием? Ответ на эти вопросы, оказывается, зависит от того, рассматриваются ли комплексные или действительные квадратичные формы. , приводится к каноническому виду
, приводится к каноническому виду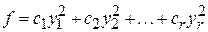 ,
,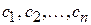 отличны от нуля. Пользуясь тем, что из всякого комплексного числа извлекается квадратный корень, выполним следующее невырожденное линейное преобразование:
отличны от нуля. Пользуясь тем, что из всякого комплексного числа извлекается квадратный корень, выполним следующее невырожденное линейное преобразование: при
при  ;
;  при
при 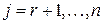 .
. , (1)
, (1)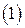 видно, что нормальный вид зависит лишь от ранга
видно, что нормальный вид зависит лишь от ранга  от
от  или
или  ,
,  ,
, отличны от нуля и положительны. Тогда невырожденное линейное преобразование с действительными коэффициентами:
отличны от нуля и положительны. Тогда невырожденное линейное преобразование с действительными коэффициентами: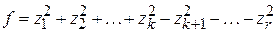 .
. двумя способами приведена к нормальному виду:
двумя способами приведена к нормальному виду: (2)
(2) был невырожденным линейным преобразованием, то обратное преобразование, выражающее
был невырожденным линейным преобразованием, то обратное преобразование, выражающее  . (3)
. (3) , (4)
, (4) , и напишем систему равенств
, и напишем систему равенств (5)
(5) линейных однородных уравнений с
линейных однородных уравнений с  .
. и все
и все  их выражениями (3) и (4), а затем подставим вместо неизвестных числа
их выражениями (3) и (4), а затем подставим вместо неизвестных числа  и
и  будут обозначены значения неизвестных
будут обозначены значения неизвестных  и
и  , получающиеся после такой подстановки, то (2) превращается, ввиду (5), в равенство
, получающиеся после такой подстановки, то (2) превращается, ввиду (5), в равенство . (6)
. (6) .
. .
. ,
, . Отсюда следует равенство
. Отсюда следует равенство  . □
. □


