Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема о матрице билинейной формы.Содержание книги Поиск на нашем сайте
Пусть L – вещественное пространство, числовая функция А(х,у) зависит от 1.A(x+z, y) = A(x,y) + A(z,y) 2.A(x;z+y) = A(x,z) + A(x,y) 3. A(λx, y) = λA(x,y); λ?R 3. A(x, λy) = λA(x,y); λ?R f(x) – линейн форма, g(y) – линейн форма => A(x,y) = f(x) g(x) – билинейн форма. опр. билин форма А(х,у) наз-ся симметричной, если для любых х,у: A(x,у) = А(у,х), наз-ся кососимметричной, если А(х,у) = - А(у,х) теор (о представлении билин формы в конечномерном пространстве): L – n-мерное пространство., Док-во: из (1) и (2) следует, что В(х,у) =
43. Преобразование матрицы билинейной формы при переходе к новому базису. Ранг билин формы. L – n-мерное пространство, теор. Пусть Док-во: элементы следствие. В(f) – матрица билинейной формы в линейном базисе е. Док-во: B(f)=c’B(e)c => с – невырожденная матрица (|c| не = 0)=> c’ – невырожд. Ранг матр при умножении на невырожд матрицу не меняется. B(e)c = rang B(f), ч.т.д. опр. Ранг билинейной формы В(х,у) в пространство L наз-ся билинейной формы относительно любого базиса опр. Билинейная форма В(х,у) в L наз-ся невырожденной, если rang [B] = dimL. Если rang [B] < dim L => вырожденная. Приведение квадратичной формы к канонич виду методом Лагранжа. опр. Пусть А(х,у) – билинейная форма, симметричная в L. Квадратичной формой наз-ся функция А(х,х) (то есть х=у), и исходная билинейная форма А(х,у) назся
Лемма о представлении билин формы в Евкл прост-ве: V – Евкл пр-во, Док-во: Докажем единственность: теор. В(х,у) - билинейн форма в Евкл прост-ве => док-во: следствие: В(х,у) – билин форма V =>
Сопряж операторы в Евклид пространстве. Самосопряж операторы и их свойства. опр. V – конечномерное Евкл прост-во. утв. А* - линейный оператор. Док-во: <Ax, λ1*y1 + λ2*y2> = <Ax, λ1*y1> + <Ax, λ2*y2> = λ1* <Ax,y1> + λ2* <Ax,y2> = λ’1*
Док-во 3: А – самосопр оператор, т.е. A=A’ и λ1, λ2, …- различн собств значения. λ1 не = λ2, х1 и х2 – соответ собств векторы => Ax1 = λ1*x1; Ax2 = λ2*x2 => <Ax1,x2> = λ1<x1,x2>; <x1, Ax2> = λ2<x1,x2>. <Ax1,x2> = <x1,Ax2> => λ1<x1,x2> = λ2 <x1,x2>; (λ1- λ2)<x1,x2>=0 по условию λ1 не = λ2 => <x1,x2?=0 => x1 ортогонально х2. ч.т.д. Нормы линейн пространства. опр. утв. Имеет место неравенство ||Ax||<=||A||*||x|| (1); Док-во: Ax = A * ((1/ ||x||)*x*||x||) ||(x/ ||x||)|| = 1, т.к. (1/||x||)*||x|| = 1 =>||Ax|| = ||(A* (1/ ||x||)* x* ||x||)|| <= sup ||Az||*||x|| = ||A||*||x|| ||Ax|| <= ||A||*||x||, ч.т.д. утв.2. А – самосопряж оператор => ||(x / ||x||) = 1 => |<Ax, (x/ ||x||)>|| <= ||A|| * ||x|| => sup|<Ax,x>| <= ||A||; |A * (x/ ||x||), (x/ ||x||)| <= A => μ = ||A|| => μ = sup |<Ax,x>| = ||A|| утв3. Док-во: утв4. А – самосопряж оператор, λ – любое собствен значение А.
утв. Любая квадратная матрица Док-во: утв. В(х,у) – симметричная билинейная форма, если В(е) симметричная матрица (необх и дост условие)
полярной к А(х,х).
теорема. Любая квадратичная форма А(х,х) в n-мерном лин пространстве L с помощью невырожденного линейного преобразования координат может быть приведена к канонич виду
Основная идея метода Лагранжа – последовательно выделяется полный квадрат по каждому аргументу. Док-во: А(х,х) не = 0, 1 шаг: А(х,х) можно преобразовать так, что коэф-т при 1-ой координаты вектора х не =0. Если а11 =0, но другие коэф-ты не =0 => при перенумерации базисного вектора а11 не =0.
пусть а11 не, в (1) выделим ту группу слагаемых, кот-е содержит х, т.е. Преобразуем выделенную сумму
(3) и (4)=>
|
||||||||||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 261; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.157.115 (0.009 с.) |

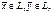 наз-ся билин формой, если явл-ся линейной по каждом из этих аргуметов.
наз-ся билин формой, если явл-ся линейной по каждом из этих аргуметов. базис => A(x,y) =
базис => A(x,y) =  (1), где
(1), где 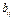 – билин форма
– билин форма  (2),
(2),  ,
, 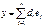 , т.е.
, т.е. 

 , ч.т. д.
, ч.т. д.
 - 2 базиса. В(е) – матрица в базисе е, B(f) – матрица билинейной формы в базисе f.
- 2 базиса. В(е) – матрица в базисе е, B(f) – матрица билинейной формы в базисе f. матрица перехода от базиса е к базису f. c’ – транспонированная матрица
матрица перехода от базиса е к базису f. c’ – транспонированная матрица 

 выражаются через
выражаются через 
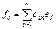 ;
;  -элементы матрицы квадратичн формы В(х,у) в е.
-элементы матрицы квадратичн формы В(х,у) в е. 
 ;
;  ;
;  -элементы В(f). B(f)=c’B(e)c, ч.т.д.
-элементы В(f). B(f)=c’B(e)c, ч.т.д.

 - ОНБ V.; h:
- ОНБ V.; h:  , k=1,…,n =>
, k=1,…,n => 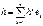 .
. 

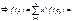
 ч.т.д.
ч.т.д. F(x)=<x,h1>, f(x) = (x,h2> => <x, h1 – h2> = 0 => x=h1 –h2 => <h1-h2,h1-h2> = 0 => (h1-h2) =0 = h1=h2 ч..т.д.
F(x)=<x,h1>, f(x) = (x,h2> => <x, h1 – h2> = 0 => x=h1 –h2 => <h1-h2,h1-h2> = 0 => (h1-h2) =0 = h1=h2 ч..т.д. B(x,y)= <x,Ay>
B(x,y)= <x,Ay> , В(х,у) – билин форма относительно х => по лемме
, В(х,у) – билин форма относительно х => по лемме  B(x,y) = <x,h>. B(x,y) = <x,Ay>. Линейность оператора вытекает из B(x, y1+y2) = <x, A(y1+y2)> = <x,Ay1> + <x,Ay2>. Докажем единственность:
B(x,y) = <x,h>. B(x,y) = <x,Ay>. Линейность оператора вытекает из B(x, y1+y2) = <x, A(y1+y2)> = <x,Ay1> + <x,Ay2>. Докажем единственность:  . B(x,y)=<x,y,>=<x,A1*y>, B(x,y)=<x,A2*y> => <x1, (A1-A2)y>=0. Пусть x=(A1 – A2)y => <(A1-A2)y, (A1-A2)y>=0 => (A1-A2)y = 0,
. B(x,y)=<x,y,>=<x,A1*y>, B(x,y)=<x,A2*y> => <x1, (A1-A2)y>=0. Пусть x=(A1 – A2)y => <(A1-A2)y, (A1-A2)y>=0 => (A1-A2)y = 0,  => A1=A2, ч.т.д.
=> A1=A2, ч.т.д. наз-ся сопряженным к линейному оператору А, если для
наз-ся сопряженным к линейному оператору А, если для 

 V – евклидово простр-во,
V – евклидово простр-во,  .
.
 ; ||Ax|| <= ||A|| * ||x||; |<Ax,x>| <= ||A|| * ||x||;
; ||Ax|| <= ||A|| * ||x||; |<Ax,x>| <= ||A|| * ||x||;  ;=> μ <= ||A|| => (1/ ||x||)* |<Ax,x>| <= ||A|| * ||x||
;=> μ <= ||A|| => (1/ ||x||)* |<Ax,x>| <= ||A|| * ||x||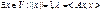
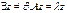 (5). Обозначим x = z/ ||z|| => ||x|| = || (z/ ||z||)|| = (1/ ||z||) * ||z|| = 1. (5) => Az = A* (x ||z||) = λ*x*||z|| => ||z||*A*x = λ*x*||z|| => Ax = λ*x = <Ax,x> = < λx, x> = λ <x, x> = λ*||x||^2 = λ => λ = <Ax,x>, ||x|| = 1, ч.т.д.
(5). Обозначим x = z/ ||z|| => ||x|| = || (z/ ||z||)|| = (1/ ||z||) * ||z|| = 1. (5) => Az = A* (x ||z||) = λ*x*||z|| => ||z||*A*x = λ*x*||z|| => Ax = λ*x = <Ax,x> = < λx, x> = λ <x, x> = λ*||x||^2 = λ => λ = <Ax,x>, ||x|| = 1, ч.т.д. опр. матрица В(е) =
опр. матрица В(е) = 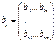 , где
, где 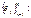
 явл-ся данным в базисе матрицы некоторой билинейной формы.
явл-ся данным в базисе матрицы некоторой билинейной формы.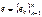 - данный базис L;
- данный базис L; 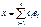 ,
, 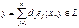 ,
, 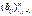 - данная матрица.
- данная матрица.  . В(х,у) – билин форма, т.е. удовлетворяет аксиомам 1-4. В(x+z, y) = В(x,y) + В(z,y);
. В(х,у) – билин форма, т.е. удовлетворяет аксиомам 1-4. В(x+z, y) = В(x,y) + В(z,y); 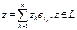 => В(x+z, y) =
=> В(x+z, y) = 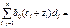
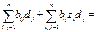 В(х,у) + В(z,y), ч.т.д.
В(х,у) + В(z,y), ч.т.д.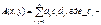 координаты вектора
координаты вектора 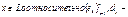 коэф-ты у относительно
коэф-ты у относительно 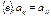 (т.к.. билинейная форма симметрична), а
(т.к.. билинейная форма симметрична), а 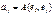 .
. матрица квадратичн формы А(е).
матрица квадратичн формы А(е).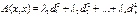 , где
, где 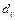 - координаты вектора
- координаты вектора 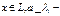 канонический коэф-т.
канонический коэф-т.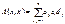 в данном базисе
в данном базисе 
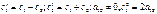


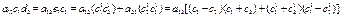
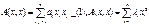


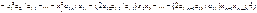
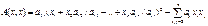 , где aij – коэф-т после преобразовния
, где aij – коэф-т после преобразовния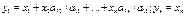
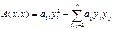 ;
;  преобразуем
преобразуем  . Повторяем этот процесс, получим в итоге квадратич форму виду
. Повторяем этот процесс, получим в итоге квадратич форму виду