Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгебраические многочлены и их корни.Содержание книги
Поиск на нашем сайте
Алгебраические многочлены и их корни. опр. алгебраическим многочленом n степени назөся выражение:
пр. Р(х) = ax^2 + bx + c; a не =0. Любой многочлен в n степени можно делить на любой многочлен в степени, не превосходящей n. пр. x^4 + 1 = (x^2 + x +1) (x^2 =) + (x+1)
док-во: (необходимость). Пусть а - корень кратности α для f(z) => a - корень кратности (α-1) для f’(z) => корень кратности (α-2) для f’’(z) =>…=> корень кратности 1 для Кроме того, а не является корнем для многочлена (достаточность) Формулы Виета
f(x)=xn+a1xn-1+a2xn-2+…+an-1x+an, и пусть a1,…,an – его корни. Þf(x)=(x-a1)…(x-an). Перемножив скобки справа, приводя подобные члены и сравн.получ-е коэфф-ты с коэфф-ми из (1), получаем рав-ва, наз-е формулами Вьета. Эти ф-лы выражают коэффициенты мног-на ч/з его корни: a1= -(a1+a2+…+an), a2=a1a2+a1a3+…+a1an+a2a3+…+an-1an, a3= -(a1a2a3+a1a2a4+…+an-2an-1an),……… an-1=(-1)n-1(a1a2…an-1+a1a2…an-2an+…+a1a2…an), an=(-1)na1a2…an. Т.О.: в правой части k-го нер-ва стоит сумма всевозм произв-й по k корней, взятая со знаком «+» или «-», в зависимости от четности или нечетности k. Если старший коэффициент а0 мног-на f(x) отличен от 1, для применения ф-л Виета нужно сначала разделить все коэфф-ты на а0, что не влияет на корни мног-на. Т.О., в этом случае
Доказать: 1) f(z)/r2(z), φ(z)/: 2) 1) Согласно (к+1) шага 2) пусть r0(z) - делитель f(z), φ(z). Доказать
Процесс нахождения НОД – алгоритм Евклида. пр. f(z)=z^4 – 2z^3 + 3z^2 – 2z +1 φ(z) = 4z^3 – 6z^2 + 6z-2 1 шаг: Делим f(z) на φ(z), получаем остаток (3/4)z^2 – (3/4)z + (3/4), частное (1/4)z-1/8 2 шаг: φ(z)=r1(z) * φ(z) + r2(z). Делим φ(z) на z^2 – z + 1, частное 4z-2, остаток=0 => НОД (f(z), φ(z))= z^2 – z + 1 НОД определяется с точностью до постоянного сомножителя Свойства делимости мног-ов: 1. если f(x) дел-ся на g(x), а g(x) дел-ся на h(x) Þ f(x) тоже дел-ся на h(x). Д-во: по усл.: f(x)= g(x)*j(х), g(x)= h(x)*y(х) Þ f(x)= h(x)[y(х)*j(х)]. 2. если f(x) и g(x) дел-ся на j(х)Þ их сумма и разность тоже дел-ся на j(х). Д-во: т.к. f(x)=j(х)*y(х) и g(x)=j(х)*c(х) Þ f(x)±g(x)=j(х)[y(х)±c(х)]
комплексного числа. опр. Комплексные числа равны, если их действ и мнимые части равны. tgφ = y/x => φ = actg (y/x) Пр. z = 1+I => x=1; y=1, |z| = √2; tgφ = 1/1=1 => φ = π/4 z = √2 (cos π/4 + isin π/4)
z1 = r1 (cosφ1 + isinφ1); z2 = r2 (cosφ2 + isinφ2) z1*z2 = r1*r2 [(cosφ1*cosφ2 – sinφ1*sinφ2) + i*(sinφ1*cosφ2 + cosφ1*sinφ2)] = r1*r2 [cos (φ1+φ2) + i*sin (φ1+φ2)] z1*z2 = |z1|*”|z2| * (cos (φ1 + φ2) + i*sin (φ1 + φ2)) if z1=z2: z^2 = |z|^2 * (cos 2φ + isin 2φ) формула Муавра:
показательная формула формула Муавра в показат форме Извлечение корня. z = r (cosφ + isinφ); W = При извлечении n корня извлекается n корень из модуля, затем [cos…] Пр.
утв. f(z), φ(z) –многочлены, причем степень φ(z) ≤ степени f(z), тогда f(z) = φ(z)*g(z) + r(z), где g(z) и r(z) – многочлены. Степень g(z) = разности степени f(z) и φ(z), а степень r(z) < степени φ(z). Вопрос о делимости f(z) на многочлен 1 степени φ(z): опр. число b является корнем f(z) если f(b)=0, b – комплексн. Если r(z) (остаток) = 0 => f(z) делится на φ(z) теор. f(z) делится на (z-b), если b является корнем f(z). Док-во: (c-const, многочлен в нулевой степени) пусть φ(z)=z-b => f(z) = φ(z)*g(z) + r(z) = (z-b)*g(z) + r(z) => (r(z)=с) =(z-b)*g(z) + c => r=b f(b) = c =0 => f(z) = φ(z) * g(z) => f(b) = 0, ч.т.д. НОД. Алгоритм Евклида. опр. НОД 2-х многочленов f(z), φ(z) назөся такой делитель, который делится на любой друой делитель этих многочленов. Пр. 12=2*2*3; 8=2*2*2 => нод=2 НОД (f(z), φ(z)) -? степень φ(z) < степени f(z) => f(z)= φ(z)*f(z) + r1(z) степень r(x) < степ φ(z), r1 – остаток. Делим φ(z) на r1(z) => φ(z)=r1(z) * φ(z) + r2(z). степень r2(z) < степ r1(z) => r1(z) = r2(z) φ2(z)+r3(z)
3. если f(x) дел-ся на j(х) Þ произв-е f(x) на " мн-н g(x) тоже дел-ся на j(х). Д-во: т.к. f(x)=j(х)*y(х) Þ f(x)*g(x)= j(х)[y(х)*g(x)] 4. из 2 и 3 Þ если " мн-н f1(x)…fк(x) дел-ся на j(х) Þ на j(х) дел-ся и мн-н f1(x)g1(x)…fк(x)gк(x), где g1(x)…gк(x) – произв мног-ны. 5. " мн-н f(x) дел-ся на " мн-н нулевой степени. Д-во: если f(x)=а0хn+a1xn-1+…an а с –произв число¹0, т.е. мн-н нулевой степени Þ f(x)=с(а0хn/с+a1xn-1/с+…an/с). 6. если f(x) дел-ся на j(х) Þ f(x) дел-ся и на с*j(х). Д-во: т.к. f(x)=j(х)*y(х) Þ f(x)=[cj(х)]*[c-1y(х)]. 7. Мн-ны сf(x), с¹0 – только они – делители мн-на f(x), имеющие такую же степень что и f(x). Д-во: f(x)=с-1[сf(x)] т.е. f(x) дел-ся на сf(x). Если же f(x) дел-ся на j(х), причем их степени совп-ют Þ степень частного от деления f(x) на j(х) должна =0, т.е. f(x)=dj(х), d¹0 Þ j(х)=d-1 f(x) Þ 8. f(x) и g(x) одноврем-но дел-ся друг на друга Û g(x)=сf(x), с¹0 9. из 1 и 8 Þ " дел-ль 1-го из 2-х мн-ов f(x), сf(x), с¹0 – дел-ль и для другого мн-на. Теорема о ранге оператора. теор. Пусть Док-во: 1) imAB ≤im A. По определению {(АВ)(х) =A(BX): im AB = { A(Bx) = Az, где теор2. Пусть следствие. пусть rangA = n => rang (AB) = rang (BA)=rang B Док-во: rang (AB) ≤ rang B, rang AB ≥ rang B (по теор2). Если в теор2 rang A =n=> rang AB = rang B, ч.т.д. rang BA ≤ rang B (теор1); rang BA ≥ rang B => rang BA = rang B если rang A = dim (im A), dim (ker A) = 0 => AB =BA Нормы линейн пространства. опр. утв. Имеет место неравенство ||Ax||<=||A||*||x|| (1); Док-во: Ax = A * ((1/ ||x||)*x*||x||) ||(x/ ||x||)|| = 1, т.к. (1/||x||)*||x|| = 1 =>||Ax|| = ||(A* (1/ ||x||)* x* ||x||)|| <= sup ||Az||*||x|| = ||A||*||x|| ||Ax|| <= ||A||*||x||, ч.т.д. утв.2. А – самосопряж оператор => ||(x / ||x||) = 1 => |<Ax, (x/ ||x||)>|| <= ||A|| * ||x|| => sup|<Ax,x>| <= ||A||; |A * (x/ ||x||), (x/ ||x||)| <= A => μ = ||A|| => μ = sup |<Ax,x>| = ||A|| утв3. Док-во: утв4. А – самосопряж оператор, λ – любое собствен значение А.
утв. Любая квадратная матрица Док-во: утв. В(х,у) – симметричная билинейная форма, если В(е) симметричная матрица (необх и дост условие)
полярной к А(х,х).
теорема. Любая квадратичная форма А(х,х) в n-мерном лин пространстве L с помощью невырожденного линейного преобразования координат может быть приведена к канонич виду Основная идея метода Лагранжа – последовательно выделяется полный квадрат по каждому аргументу. Док-во: А(х,х) не = 0, 1 шаг: А(х,х) можно преобразовать так, что коэф-т при 1-ой координаты вектора х не =0. Если а11 =0, но другие коэф-ты не =0 => при перенумерации базисного вектора а11 не =0.
пусть а11 не, в (1) выделим ту группу слагаемых, кот-е содержит х, т.е. Преобразуем выделенную сумму
(3) и (4)=>
Алгебраические многочлены и их корни. опр. алгебраическим многочленом n степени назөся выражение:
пр. Р(х) = ax^2 + bx + c; a не =0. Любой многочлен в n степени можно делить на любой многочлен в степени, не превосходящей n. пр. x^4 + 1 = (x^2 + x +1) (x^2 =) + (x+1)
док-во: (необходимость). Пусть а - корень кратности α для f(z) => a - корень кратности (α-1) для f’(z) => корень кратности (α-2) для f’’(z) =>…=> корень кратности 1 для Кроме того, а не является корнем для многочлена (достаточность) Формулы Виета
f(x)=xn+a1xn-1+a2xn-2+…+an-1x+an, и пусть a1,…,an – его корни. Þf(x)=(x-a1)…(x-an). Перемножив скобки справа, приводя подобные члены и сравн.получ-е коэфф-ты с коэфф-ми из (1), получаем рав-ва, наз-е формулами Вьета. Эти ф-лы выражают коэффициенты мног-на ч/з его корни: a1= -(a1+a2+…+an), a2=a1a2+a1a3+…+a1an+a2a3+…+an-1an, a3= -(a1a2a3+a1a2a4+…+an-2an-1an),……… an-1=(-1)n-1(a1a2…an-1+a1a2…an-2an+…+a1a2…an), an=(-1)na1a2…an. Т.О.: в правой части k-го нер-ва стоит сумма всевозм произв-й по k корней, взятая со знаком «+» или «-», в зависимости от четности или нечетности k. Если старший коэффициент а0 мног-на f(x) отличен от 1, для применения ф-л Виета нужно сначала разделить все коэфф-ты на а0, что не влияет на корни мног-на. Т.О., в этом случае
Доказать: 1) f(z)/r2(z), φ(z)/: 2) 1) Согласно (к+1) шага 2) пусть r0(z) - делитель f(z), φ(z). Доказать
Процесс нахождения НОД – алгоритм Евклида. пр. f(z)=z^4 – 2z^3 + 3z^2 – 2z +1 φ(z) = 4z^3 – 6z^2 + 6z-2 1 шаг: Делим f(z) на φ(z), получаем остаток (3/4)z^2 – (3/4)z + (3/4), частное (1/4)z-1/8 2 шаг: φ(z)=r1(z) * φ(z) + r2(z). Делим φ(z) на z^2 – z + 1, частное 4z-2, остаток=0 => НОД (f(z), φ(z))= z^2 – z + 1 НОД определяется с точностью до постоянного сомножителя Свойства делимости мног-ов: 1. если f(x) дел-ся на g(x), а g(x) дел-ся на h(x) Þ f(x) тоже дел-ся на h(x). Д-во: по усл.: f(x)= g(x)*j(х), g(x)= h(x)*y(х) Þ f(x)= h(x)[y(х)*j(х)]. 2. если f(x) и g(x) дел-ся на j(х)Þ их сумма и разность тоже дел-ся на j(х). Д-во: т.к. f(x)=j(х)*y(х) и g(x)=j(х)*c(х) Þ f(x)±g(x)=j(х)[y(х)±c(х)]
комплексного числа. опр. Комплексные числа равны, если их действ и мнимые части равны. tgφ = y/x => φ = actg (y/x) Пр. z = 1+I => x=1; y=1, |z| = √2; tgφ = 1/1=1 => φ = π/4 z = √2 (cos π/4 + isin π/4)
z1 = r1 (cosφ1 + isinφ1); z2 = r2 (cosφ2 + isinφ2) z1*z2 = r1*r2 [(cosφ1*cosφ2 – sinφ1*sinφ2) + i*(sinφ1*cosφ2 + cosφ1*sinφ2)] = r1*r2 [cos (φ1+φ2) + i*sin (φ1+φ2)] z1*z2 = |z1|*”|z2| * (cos (φ1 + φ2) + i*sin (φ1 + φ2)) if z1=z2: z^2 = |z|^2 * (cos 2φ + isin 2φ) формула Муавра:
показательная формула формула Муавра в показат форме Извлечение корня. z = r (cosφ + isinφ); W = При извлечении n корня извлекается n корень из модуля, затем [cos…] Пр.
утв. f(z), φ(z) –многочлены, причем степень φ(z) ≤ степени f(z), тогда f(z) = φ(z)*g(z) + r(z), где g(z) и r(z) – многочлены. Степень g(z) = разности степени f(z) и φ(z), а степень r(z) < степени φ(z). Вопрос о делимости f(z) на многочлен 1 степени φ(z): опр. число b является корнем f(z) если f(b)=0, b – комплексн. Если r(z) (остаток) = 0 => f(z) делится на φ(z) теор. f(z) делится на (z-b), если b является корнем f(z). Док-во: (c-const, многочлен в нулевой степени) пусть φ(z)=z-b => f(z) = φ(z)*g(z) + r(z) = (z-b)*g(z) + r(z) => (r(z)=с) =(z-b)*g(z) + c => r=b f(b) = c =0 => f(z) = φ(z) * g(z) => f(b) = 0, ч.т.д.
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 337; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.18.59 (0.007 с.) |

 , С1 – комплексное число, z – переменная, комплексн.
, С1 – комплексное число, z – переменная, комплексн.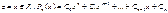

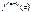 , т.е. f(a) = 0, f’(a) = 0,
, т.е. f(a) = 0, f’(a) = 0, 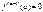
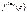 , т.е.
, т.е. 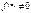
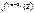 => … => а - корень кратности не ниже α для f(z) => если а корень кратности > α,
=> … => а - корень кратности не ниже α для f(z) => если а корень кратности > α, 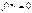 - противоречие => теорема доказана.
- противоречие => теорема доказана.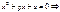
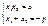

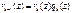 - остаток = 0
- остаток = 0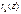 - НОД (f(z), φ(z))
- НОД (f(z), φ(z))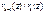 => согласно шагу (к)
=> согласно шагу (к) 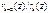 , т.к.
, т.к. 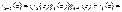

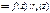 и
и 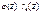 , ч.т.д.
, ч.т.д.
 => r2(z):r0(z) =>
=> r2(z):r0(z) => 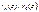 =>
=> 
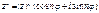
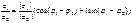
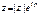 , формула Эйлера -
, формула Эйлера - 
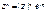
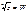 ; W = ρ (cos ψ +isin ψ) => z = W^n => W^n = (ρ^n) (cos ψ +isin ψ) => r (cosφ + isinφ) = (ρ^n) (cos ψ +isin ψ) => r = ρ; φ+2kπ = nψ k=0,1…(n-1) => ψ = (φ + 2kπ)/n
; W = ρ (cos ψ +isin ψ) => z = W^n => W^n = (ρ^n) (cos ψ +isin ψ) => r (cosφ + isinφ) = (ρ^n) (cos ψ +isin ψ) => r = ρ; φ+2kπ = nψ k=0,1…(n-1) => ψ = (φ + 2kπ)/n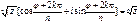


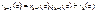

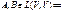 1) rang AB ≤ rang A 2) rang AB ≤ rang B
1) rang AB ≤ rang A 2) rang AB ≤ rang B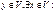 (AB)(x)=y} =
(AB)(x)=y} = 
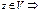 у явл-ся образом А: у ≤ im A (y=Az,
у явл-ся образом А: у ≤ im A (y=Az, 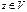 ) => 1) dim (im AB) ≤ dim (im A) => rang AB ≤ rang A,.ч.т.д. 2) ker B ≤ ker AB (т.к.: пусть
) => 1) dim (im AB) ≤ dim (im A) => rang AB ≤ rang A,.ч.т.д. 2) ker B ≤ ker AB (т.к.: пусть  => Bx = 0=> A(Bx) = 0 =>
=> Bx = 0=> A(Bx) = 0 => 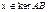 ) => dim ker B ≤ dim ker (AB) => dim V – dim (kerAB) ≥ dimV – dim (ker AB) => dim (im AB) ≤ dim (im B) => rang AB ≤ rang B
) => dim ker B ≤ dim ker (AB) => dim V – dim (kerAB) ≥ dimV – dim (ker AB) => dim (im AB) ≤ dim (im B) => rang AB ≤ rang B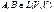 , dim V = n => rang (AB) ≥ rang A + rang B - n
, dim V = n => rang (AB) ≥ rang A + rang B - n V – евклидово простр-во,
V – евклидово простр-во,  .
.
 ; ||Ax|| <= ||A|| * ||x||; |<Ax,x>| <= ||A|| * ||x||;
; ||Ax|| <= ||A|| * ||x||; |<Ax,x>| <= ||A|| * ||x||;  ;=> μ <= ||A|| => (1/ ||x||)* |<Ax,x>| <= ||A|| * ||x||
;=> μ <= ||A|| => (1/ ||x||)* |<Ax,x>| <= ||A|| * ||x||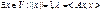
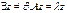 (5). Обозначим x = z/ ||z|| => ||x|| = || (z/ ||z||)|| = (1/ ||z||) * ||z|| = 1. (5) => Az = A* (x ||z||) = λ*x*||z|| => ||z||*A*x = λ*x*||z|| => Ax = λ*x = <Ax,x> = < λx, x> = λ <x, x> = λ*||x||^2 = λ => λ = <Ax,x>, ||x|| = 1, ч.т.д.
(5). Обозначим x = z/ ||z|| => ||x|| = || (z/ ||z||)|| = (1/ ||z||) * ||z|| = 1. (5) => Az = A* (x ||z||) = λ*x*||z|| => ||z||*A*x = λ*x*||z|| => Ax = λ*x = <Ax,x> = < λx, x> = λ <x, x> = λ*||x||^2 = λ => λ = <Ax,x>, ||x|| = 1, ч.т.д.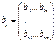 , где
, где 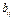 - из (2), наз-ся матрицей линейно формы В(х,у) в базисе
- из (2), наз-ся матрицей линейно формы В(х,у) в базисе 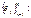
 явл-ся данным в базисе матрицы некоторой билинейной формы.
явл-ся данным в базисе матрицы некоторой билинейной формы.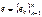 - данный базис L;
- данный базис L; 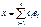 ,
, 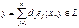 ,
, 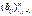 - данная матрица.
- данная матрица.  . В(х,у) – билин форма, т.е. удовлетворяет аксиомам 1-4. В(x+z, y) = В(x,y) + В(z,y);
. В(х,у) – билин форма, т.е. удовлетворяет аксиомам 1-4. В(x+z, y) = В(x,y) + В(z,y); 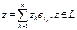 => В(x+z, y) =
=> В(x+z, y) = 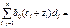
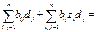 В(х,у) + В(z,y), ч.т.д.
В(х,у) + В(z,y), ч.т.д.
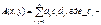 координаты вектора
координаты вектора 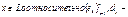 коэф-ты у относительно
коэф-ты у относительно 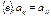 (т.к.. билинейная форма симметрична), а
(т.к.. билинейная форма симметрична), а 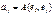 .
. матрица квадратичн формы А(е).
матрица квадратичн формы А(е).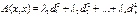 , где
, где 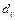 - координаты вектора
- координаты вектора 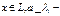 канонический коэф-т.
канонический коэф-т.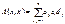 в данном базисе
в данном базисе 
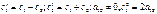


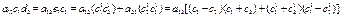
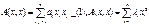


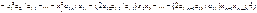
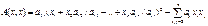 , где aij – коэф-т после преобразовния
, где aij – коэф-т после преобразовния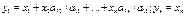
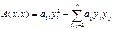 ;
;  преобразуем
преобразуем  . Повторяем этот процесс, получим в итоге квадратич форму виду
. Повторяем этот процесс, получим в итоге квадратич форму виду