
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейные операторы и их свойства. Обратный оператор.Содержание книги
Поиск на нашем сайте
опр. W1, W2 – произвольные линейные пространства, соответствующих размерностей n и m. Оператором А из V в W наз-ся отображение вида А: V →W опр. оператор А, действующий V →W, наз-ся линейным, если для любых х1, х2 и λ (чисел) опр. образом линейн оператора А, действующего V →W, наз-ся множество Сумма операторов и умножение на число. А: V →W; В: V →W (А + В)(х) = Ах+Вх (λ)(А)(х) = λ (Ах); λ
утв. если (A^(-1))*A*x=0, то х=0 опр. Говорят, что линейн оператор утв. пусть Док-во: теор. Чтобы Док-во: (необх) пусть сущест-ет А^(-1). Предположим противное, А не явл-ся взаимнооднозначным Ах1-Ах2 = А(х1-х2)=0 => x1-x2=0 при х1 не = х2 => несоответствие => А – взаимооднозн, ч.т.д. (достаточн) Пусть А: V → V: осущ-ет взаимноодназн отображение. Надо доказать,ч то сущест-ет А^(-1).
p=dimV1 => p ≥ q. p>q – противоречие. (докажем, что противоречие). Пусть p>q, => p=q => dimV1 = dim (imA) => dim (im A) +dim (ker A) =n опр. rang A = dim (im A). рангом оператора наз-ся число, равное размерности образа этого оператора. следствие. Чтобы док-во: по теор1 dim (imA) + dim (ker A) = n. dim (im A)=n, rang A=n => dim (ker A) =0 => dim (ker A) = 0 => ker – θ => А взаимооднозначно V => теор2. Пусть Док-во: пусть dim V1 = p; dim V2 = q.
A- линейн, тк Теорема о ранге оператора. теор. Пусть Док-во: 1) imAB ≤im A. По определению {(АВ)(х) =A(BX): im AB = { A(Bx) = Az, где теор2. Пусть следствие. пусть rangA = n => rang (AB) = rang (BA)=rang B Док-во: rang (AB) ≤ rang B, rang AB ≥ rang B (по теор2). Если в теор2 rang A =n=> rang AB = rang B, ч.т.д. rang BA ≤ rang B (теор1); rang BA ≥ rang B => rang BA = rang B если rang A = dim (im A), dim (ker A) = 0 => AB =BA
|
|||||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 274; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.175.191 (0.006 с.) |

 1) А (х1 + х2) = Ах1 + Ах2 (свойство адитивности) 2) А(λч) = λАч (однородность)
1) А (х1 + х2) = Ах1 + Ах2 (свойство адитивности) 2) А(λч) = λАч (однородность) у=Ах. im A = {
у=Ах. im A = {  }.
}.
 опр. нулевым оператором θ:
опр. нулевым оператором θ: 
 действует взаимнооднозначно V → V, если 2-м разл элементам х1 не = х2 (из V) → Ах1 не = Ах2. Отображение на: V на V отображает оператор А в этом случае, т.е.
действует взаимнооднозначно V → V, если 2-м разл элементам х1 не = х2 (из V) → Ах1 не = Ах2. Отображение на: V на V отображает оператор А в этом случае, т.е. 
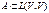 взаимнооднозначное отображение =>
взаимнооднозначное отображение =>  ө линейно независимые элементы простр-ва V →
ө линейно независимые элементы простр-ва V →  - лин незав элементы V.
- лин незав элементы V. -лин независ =>
-лин независ => 

 =>
=>  =>
=>  отсюда вытекает отображение на =>
отсюда вытекает отображение на =>  - лин незав, ч.т.д.
- лин незав, ч.т.д. , т.е. х1 – х2 не = о, но Ах1=Ах2.
, т.е. х1 – х2 не = о, но Ах1=Ах2. =>
=>  . А^(-1) – лин оператор => обратн оператор (согласно определению).
. А^(-1) – лин оператор => обратн оператор (согласно определению). - лин незав V1 дополним
- лин незав V1 дополним  так, чтобы
так, чтобы  - линейн незав в V1.
- линейн незав в V1.  =>
=>  не все =0:
не все =0: 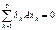 =>
=>  =>
=>  но
но  имел A^(-1) необход и дост, чтобы rang A = dim V = n
имел A^(-1) необход и дост, чтобы rang A = dim V = n
 (подпространства), где dimV =n. dim V1+dimV2=dimV =>
(подпространства), где dimV =n. dim V1+dimV2=dimV =>  V1 = im A, V2 = ker A
V1 = im A, V2 = ker A - базис V такой,чтобы
- базис V такой,чтобы  в V1
в V1 

 A: Ae1=g1, Ae2=g2,
A: Ae1=g1, Ae2=g2,  ,
,  =>
=>  =>
=> 
 => V1= im A = {
=> V1= im A = { 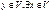 ; Ax=y}
; Ax=y} А(х+у) = Ах +Ау
А(х+у) = Ах +Ау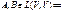 1) rang AB ≤ rang A 2) rang AB ≤ rang B
1) rang AB ≤ rang A 2) rang AB ≤ rang B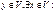 (AB)(x)=y} =
(AB)(x)=y} = 
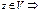 у явл-ся образом А: у ≤ im A (y=Az,
у явл-ся образом А: у ≤ im A (y=Az, 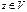 ) => 1) dim (im AB) ≤ dim (im A) => rang AB ≤ rang A,.ч.т.д. 2) ker B ≤ ker AB (т.к.: пусть
) => 1) dim (im AB) ≤ dim (im A) => rang AB ≤ rang A,.ч.т.д. 2) ker B ≤ ker AB (т.к.: пусть  => Bx = 0=> A(Bx) = 0 =>
=> Bx = 0=> A(Bx) = 0 => 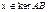 ) => dim ker B ≤ dim ker (AB) => dim V – dim (kerAB) ≥ dimV – dim (ker AB) => dim (im AB) ≤ dim (im B) => rang AB ≤ rang B
) => dim ker B ≤ dim ker (AB) => dim V – dim (kerAB) ≥ dimV – dim (ker AB) => dim (im AB) ≤ dim (im B) => rang AB ≤ rang B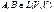 , dim V = n => rang (AB) ≥ rang A + rang B - n
, dim V = n => rang (AB) ≥ rang A + rang B - n


