
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приведение квадратич формы к канонич виду методом ортогонСодержание книги
Поиск на нашем сайте
виду 1) метолом Лагранжа 2) методом ортогонал преобразований Решение: 1) Применим к W(x1,x3), соберем все члены в группу:
т.о. получим
собств вектора
Док-во: а11*(х^2)+а12*х*у+а22*(у^2) A = (a11 a12 = (а11 а12 a21 a22) а12 а22) привести к канонич виду методом ортогон преобразований. (х = Р * (х’ Р – ортогон матр= (Р11 Р12 у) y’) (1) Р21 Р22) λ1*((x’)^2)+ λ2*((y’)^2); λ – собств значение матр А. столбцами Р явл-ся соответст собств векторы А. Р – ортогон матрица => (система): (P11)^2 + (P21)^2 = 1; (P12)^2 + (P22)^2 = 1; P11*P12 + P21*P22=0 P11=cos φ; P21= sin φ; P12 = cos ψ; P21 = sinψ cos φ * cos ψ + sin φ * sinψ =0 cos (φ – ψ)=0 => (φ – ψ)=± (π/4) + πk; φ= ψ – (π/2); cos ψ= cos (φ + (π/2)) = sin φ P = (cos φ sin φ sin φ cos φ) -> преобразование поворота на φ в ОХУ: ĩ, ĵ (базисн векторы) переходит в прямоуг систему ОХ’У c ĩ’, ĵ’ (базисн векторы), причем (ĩ’, ĵ’) = (ĩ, ĵ)Р i = cos φ * ĩ’ + sin φ * ĵ’ j = - sin φ * ĩ’ + cos φ * ĵ’ через (1) выразим 2*b1*x + 2*b1*y через координаты x’, y’ => λ1 * ((x’)^2) + λ2 * ((y’)^2) + 2*b1*(x’) + 2*b1* (y’) + c =0; выделим полный квадрат относительно x’ и y’: λ1* (x’ + ĩ1)^2 + λ2 * (y’ + ĩ2) + c =0 λ1*(x’’)^2 + λ2* (y’’)^2 + c =0 пр. 11*x^2 – 20*x*y – 4*y^2 20*x – 8*y +1=0 привести к канон виду с помощью
преобразований. Закон инерции квадрат формы.
пр. A(x,x)=
теор. Пр.
2)
нормизуем х1: собств вектор если λ=4:
Закон инерции квадратичн формы: независимо от способа приведения квадр формы к канонич виду, число е положительно и число ее положительных, а также отриц-х коэффициентов постоянны.
Приведение к канонич виду уравнения кривой 2 порядка. Приведение к канонич виду уравнений поверхности 2 порядка. опр. Уравнение кривой 2-го порядка в прямоугольной системе координат ОХУ имеет след вид: а11*(х^2)+а12*х*у+а22*(у^2)+2*b1*x+2*b2y+c=0;
повороту ОХУ и параллельного переноса. 1 шаг: 11*x^2 – 20*x*y – 4*y^2; A= (11 -10 (11-λ -10 -10 -4) x=Py; P -? -10 4- λ) = 0 => λ1=-9; λ2=16 det [(A- λ*I)x]=0 |20x -10| |-10 -5x| =0 P= | |2 (20 -10 -10 5) => (система) 20x -10y=0; -10x+5y=0 => y=2x; x=1, y=2; z(x,y) => |z|= вектор (1/ (-5 -10 (х -10 -10) * у) = (система) -5x-10y=0; -10x-10y=0 => x=-2y=> y=1; x=-2 вектор (-2/ Р = (1/ 2/ (x| |x’| |1/
(система) x= 11/ λ1 ((x’)^2) + -9 (x’)^2 + 16*(y’)^2 – 36/ -9 (x’+ 2/ -9 (x’)^2 – 36/ ║перенос; x’+ 2/ y’ + 1/ Уравнение поверхности 2-го порядка: а11*(x^2)+ a22*(y^2)+a33*(z^2)+2*a12*x*y+ 2*a23*y*z+ 2*b1*x + 2*b2*y + 2*b1*z + c=0 |x| |x’| |y| = P* |y’| λ1- собств значение А |z’| A(x,y,z)= λ1*(x’)^2 + λ2 (y’)^2 + λ3* (z’)^2 A= |a11 a12 a13| |a21 a22 a23| |a31 a31 a33| симметр матрица. С помощью паралл переноса,
замены x,y,z на x’, y’, z’ => λ1*(x’’)^2 + λ2*(y’’)^2 + λ3* (z’’)^2=c
|
||||||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 220; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |


 дополним до полного квадрата
дополним до полного квадрата 
 ;
; 




 ;
;  ;
; 


 ; <x2,x3>=-1+1+1=0 => x2┴x1; <x3,x1>=0; HO <x2,x3>=0,25 => x2 HE ┴ x1
; <x2,x3>=-1+1+1=0 => x2┴x1; <x3,x1>=0; HO <x2,x3>=0,25 => x2 HE ┴ x1 ;х=Ру:
;х=Ру: 
 ;
;  ;
;  ;
;  ;
;

 матрица квадратичн формы.
матрица квадратичн формы.
 ;
;  ; x=Py
; x=Py если матрица Р невырожденная, то
если матрица Р невырожденная, то  если det P =0 (вырожденное линейное преобразование), х=РУ – ортогон преобразование, если Р – ортогон матрица, т.е.элементы строк(столбцов) попарно ортогональны
если det P =0 (вырожденное линейное преобразование), х=РУ – ортогон преобразование, если Р – ортогон матрица, т.е.элементы строк(столбцов) попарно ортогональны 
 ортогон преобразование х=РУ, приводящее ее к канонич виду,т.е. квадр форме
ортогон преобразование х=РУ, приводящее ее к канонич виду,т.е. квадр форме  , (i= 1…n – собств знач матрицы А, а столбцы Р – ортогональные нормированные собств векторы м-цы А)
, (i= 1…n – собств знач матрицы А, а столбцы Р – ортогональные нормированные собств векторы м-цы А) привести к канонич)
привести к канонич)

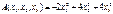 ; rang=2 если λ=-2:
; rang=2 если λ=-2:  ;
;  ;
; 

 пусть х2=1, x3=0 =>x1=0,5: пусть х2=0, х3=0 =>х1= 0,5
пусть х2=1, x3=0 =>x1=0,5: пусть х2=0, х3=0 =>х1= 0,5


 (без док-ва)
(без док-ва) ,
,  и с – коэф-ты квадратичной формы.
и с – коэф-ты квадратичной формы.
 -2
-2  |
| -11
-11  | λ1=-9
| λ1=-9 )
) 2/
2/ 
 |y) = P* |y’| = |2/
|y) = P* |y’| = |2/ 



