
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приведение квадратичной формы к каноническому видуСодержание книги
Поиск на нашем сайте
При помощи линейной замены переменных квадратичную форму Покажем, как это сделать. Пусть
На предложенном пути, уже с самого начала, могут возникнуть некоторые трудности. Например, может оказаться, что Предложенные выше преобразования переменных линейны, то есть могут быть представлены равенством Описанный выше метод приведения квадратичной формы к каноническому виду называется методом Лагранжа. Задача приведения квадратичной формы к каноническому виду решается неоднозначно. Тем не менее, имеет место закон инерции квадратичных форм, а именно, справедлива следующая теорема. Т е о р е м а. Каким бы способом ни приводилась квадратичная форма к каноническому виду, количество квадратов с положительными, отрицательными и нулевыми коэффициентами остаётся неизменным. Продемонстрируем идею доказательства этой теоремы на примере. Допустим, что квадратичная форма Используя тот факт, что числа положительных коэффициентов не совпадают, найдём такой ненулевой вектор X, что преобразования Для этого рассмотрим систему уравнений
В этой системе количество уравнений с коэффициентами pi j из матрицы P (первые две строчки) совпадает с числом положительных коэффициентов в первом представлении квадратичной формы, а количество уравнений с коэффициентами Так как во втором представлении положительных коэффициентов больше, чем в первом, то сумма числа положительных коэффициентов первого представления и неположительных – второго, меньше числа переменных. Так что рассматриваемая однородная система содержит неизвестных больше, чем уравнений, и, следовательно, имеет нетривиальное (ненулевое) решение X = (x 1, x 2, x 3, x 4, x 5, x 6, x7)Τ. Очевидно, что преобразования значения квадратичных форм Умножив все три формы на минус единицу, получим, что оба канонических представления исходной квадратичной формы имеют одинаковое число отрицательных коэффициентов. Ясно, что тогда совпадают и числа нулевых коэффициентов. Существует ещё один метод приведения квадратичной формы к каноническому виду. Он основан на особых свойствах собственных чисел и собственных векторов симметричных матриц. Рассмотрим этот метод для случая симметричной матрицы третьего порядка (назовём её A), имеющей три различных собственных числа Будем считать, что эти векторы нормированы (вектор Покажем, что векторы
Приравняем правые части: Поскольку Покажем, что векторы
Рассмотрим матрицу P = (X 1 X 2 X 3), столбцами которой служат векторы P Τ P = Теперь предположим, что A – матрица некоторой квадратичной формы. Произведём линейную замену переменных X = PY. Матрица
Таким образом, замена X = PY приводит матрицу квадратичной формы к диагональному виду. Покажем, что при такой замене собственные векторы исходной матрицы преобразуются в собственные векторы новой матрицы. Равенство X = PY эквивалентно равенству Аналогично вводятся векторы Пример. Приведём к каноническому виду квадратичную форму С этой целью вычислим определитель
Таким образом, характеристическое уравнение матрицы A имеет вид Собственный вектор
При Суммы квадратов координат векторов Тогда
преобразование
Таким образом, исходная квадратичная форма приводится к виду Приведение к каноническому виду можно осуществить методом Лагранжа:
Здесь Квадратичные формы
|
||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 373; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.239.70 (0.006 с.) |

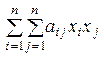 можно привести к каноническому виду
можно привести к каноническому виду  .
. . Сгруппируем слагаемые, содержащие
. Сгруппируем слагаемые, содержащие  и, вынеся предварительно
и, вынеся предварительно  за скобки, выделим полный квадрат, используя формулу квадрата суммы:
за скобки, выделим полный квадрат, используя формулу квадрата суммы:  . Соответствующие преобразования выглядят так:
. Соответствующие преобразования выглядят так: 
 Заменив затем переменные по формулам
Заменив затем переменные по формулам 
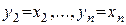 , получим, что
, получим, что  .
.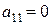 . В этом случае нужно поменять местами первую переменную с той, коэффициент при квадрате которой отличен от нуля. Если коэффициенты при всех квадратах нулевые, то найдётся произведение каких-нибудь двух переменных с отличным от нуля коэффициентом (в противном случае квадратичная форма тождественно равна нулю). Не умаляя общности, можно считать, что
. В этом случае нужно поменять местами первую переменную с той, коэффициент при квадрате которой отличен от нуля. Если коэффициенты при всех квадратах нулевые, то найдётся произведение каких-нибудь двух переменных с отличным от нуля коэффициентом (в противном случае квадратичная форма тождественно равна нулю). Не умаляя общности, можно считать, что  . Положим
. Положим  . Слагаемое
. Слагаемое 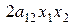 при этом приобретает вид
при этом приобретает вид  . После этого можно выполнить действия, описанные выше для случая, когда коэффициент при квадрате первой переменной отличен от нуля. В результате мы получаем сумму квадрата первой переменной с ненулевым коэффициентом и новой квадратичной формы с n –1 переменной. Далее процесс продолжается аналогично.
. После этого можно выполнить действия, описанные выше для случая, когда коэффициент при квадрате первой переменной отличен от нуля. В результате мы получаем сумму квадрата первой переменной с ненулевым коэффициентом и новой квадратичной формы с n –1 переменной. Далее процесс продолжается аналогично.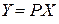 (или
(или  ), где P – невырожденная матрица, а
), где P – невырожденная матрица, а 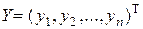 и
и  – столбцы, соответственно, новых и старых переменных. В первом случае
– столбцы, соответственно, новых и старых переменных. В первом случае 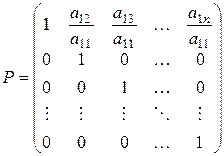 ,во втором
,во втором  .
. при помощи преобразования
при помощи преобразования 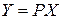 приведена к виду
приведена к виду  , а при помощи преобразования
, а при помощи преобразования  – к виду
– к виду  .
. и
и  и
и  соответственно.
соответственно. .
.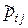 из матрицы
из матрицы  (последние три строчки) совпадает с числом неположительных коэффициентов во втором представлении.
(последние три строчки) совпадает с числом неположительных коэффициентов во втором представлении.
 и
и  при найденных X, Y и Z (соответственно) совпадают, вместе с тем значение
при найденных X, Y и Z (соответственно) совпадают, вместе с тем значение  ,
,  ,
,  и, соответственно, три собственных вектора:
и, соответственно, три собственных вектора:  ,
,  ,
,  .
. называется нормированным, если
называется нормированным, если 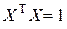 , то есть, если
, то есть, если  ).
).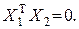 преобразуем произведение
преобразуем произведение  двумяспособами:
двумяспособами: и
и  .
. . Отсюда
. Отсюда  .
. ,
,  , так что равно нулю произведение
, так что равно нулю произведение  . Ортогональность
. Ортогональность 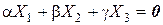 . Умножив обе части этого равенства на
. Умножив обе части этого равенства на 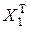 слева, получим, что
слева, получим, что  . Учитывая нормированность вектора
. Учитывая нормированность вектора  , следовательно, α = 0. Так же доказывается, что β = 0 и γ = 0. Это означает, что векторы
, следовательно, α = 0. Так же доказывается, что β = 0 и γ = 0. Это означает, что векторы  ). Действительно,
). Действительно,
 новой квадратичной формы равна, как известно, P Τ AP. Воспользуемся тем, что матрица P составлена из собственных векторов матрицы A. Тогда
новой квадратичной формы равна, как известно, P Τ AP. Воспользуемся тем, что матрица P составлена из собственных векторов матрицы A. Тогда 

 . Пусть
. Пусть  , тогда
, тогда 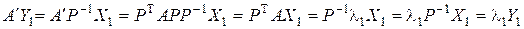 .
. ,
, 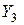 и доказывается, что это собственные векторы матрицы
и доказывается, что это собственные векторы матрицы  . Выпишем матрицу коэффициентов A =
. Выпишем матрицу коэффициентов A =  . Найдём характеристическое уравнение матрицы A.
. Найдём характеристическое уравнение матрицы A. .
.
 . Его корнями являются
. Его корнями являются  ,
,  ,
,  .
.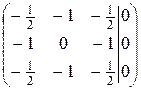 ~
~  . Положим его первую координату равной единице, тогда
. Положим его первую координату равной единице, тогда  . собственный вектор
. собственный вектор  ~
~  ~
~  ~
~ 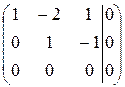 . Положим его третью координату равной единице, тогда
. Положим его третью координату равной единице, тогда  .
. имеем
имеем 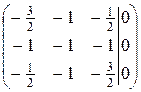 ~
~ 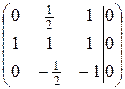 ~
~  . Полагая третью координату равной единице, получаем, что
. Полагая третью координату равной единице, получаем, что  .
. , соответственно. Получим
, соответственно. Получим 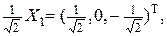

 .
. . Убедимся в ортогональности этой матрицы, умножив её на транспонированную.
. Убедимся в ортогональности этой матрицы, умножив её на транспонированную. .
.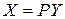 , или
, или  , даёт новую квадратичную форму с матрицей
, даёт новую квадратичную форму с матрицей  . Вычислим матрицу
. Вычислим матрицу  .
.

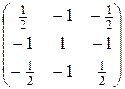

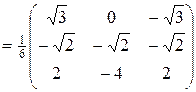
 =
= 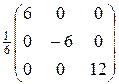 =
=  .
. .
.

 , откуда
, откуда  . Если
. Если  , то
, то  . Заметим, что матрица Q ортогональной не является.
. Заметим, что матрица Q ортогональной не является. отличаются коэффициентами, но количество положительных (два) и отрицательных (один) коэффициентов при квадратах переменных у них совпадает.
отличаются коэффициентами, но количество положительных (два) и отрицательных (один) коэффициентов при квадратах переменных у них совпадает.


