
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение систем линейных уравнений методом ГауссаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Пусть имеется система линейных уравнений. Очевидно, что если к одному из уравнений системы прибавить другое, мысленно умноженное на какое-нибудь число, получится система, равносильная данной. Не нарушают равносильности также умножение обеих частей одного из уравнений на число, отличное от нуля, и перестановка уравнений. Этим действиям с уравнениями системы отвечают допустимые действия со строками так называемой расширенной матрицысистемы. Расширенной матрицей системы называется матрица коэффициентов при неизвестных A, к которой присоединён столбец свободных членов B, отделённый от A вертикальной чертой. Расширенная матрица имеет вид К преобразованиям, не нарушающим равносильности, можно отнести изменение нумерации неизвестных. Изменению нумерации неизвестных отвечает перестановка столбцов, составленных из коэффициентов при этих неизвестных. Поэтому перестановка столбцов, не затрагивающая столбца свободных членов, также относится к допустимым преобразованиям. Сначала рассмотрим метод Гаусса на примере системы трёх линейных уравнений с тремя неизвестными в предположении, что главный определитель системы отличен от нуля[*]. В этом случае суть метода Гаусса состоит в преобразовании данной системы в систему с треугольной матрицей. Для системы Схематично метод Гаусса можно изобразить так: Первый этап Второй этап Третий этап
Преобразования можно продолжить с целью получить систему с единичной матрицей. В этом случае говорят о методе Гаусса-Жордана.
Третий этап Четвёртый этап Пятый этап Пример. Пусть дана система Выпишем расширенную матрицу и выполним нужные преобразования: ~ Последняя матрица соответствует системе Метод Гаусса-Жордана отличается от метода Гаусса тем, что вычисление неизвестных производится в матричной форме. Матрица
Рассмотрим теперь метод Гаусса в ситуации, когда либо число уравнений не совпадает с числом неизвестных, либо неизвестно, отличен ли от нуля главный определитель системы. Приведём при помощи допустимых преобразований расположенную до черты часть расширенной матрицы исследуем систему с такой расширенной матрицей на совместность. Если Во всех остальных случаях система совместна. Рассмотрим эти случаи.
Если Имеется два варианта:
Пусть Однородные (с нулевыми правыми частями) системы линейных уравнений всегда совместны, поскольку имеют нулевое (состоящее из нулей) решение. Это решение единственно, если Отметим, что во всех случаях, когда система совместна, матрица Пример. Пусть расширенная матрица некоторой системы линейных уравнений при помощи допустимых преобразований приведена к виду Если в столбце свободных членов третий или четвёртый элемент был бы не 0, а, например, 1, то система была бы несовместной, так как одно из её уравнений имело бы вид: Ранг матрицы Число r называется рангом матрицы A ( Иными словами, рангом матрицы называется наивысший порядок отличных от нуля миноров. Ранг матрицы, состоящий из нулей, считается равным нулю. Ранг невырожденной квадратной матрицы n -го порядка равен n. В частности, ранг треугольной матрицы равен её порядку. Ранг матрицы размерности Например, Очевидно, что ранг матрицы не изменяется при транспонировании.
легко найти ранг матрицы, имеющей канонический или почти канонический вид. Очевидно, что ранг такой матрицы равен k. Действительно, единичная матрица даёт нам минор k -го порядка, отличный от нуля, а любой минор (k +1)-го порядка равен нулю, так как содержит строку, состоящую из нулей. приведение матрицы к каноническому или почти каноническому виду – один из способов вычисления её ранга, основанный на следующей теореме. Т е о р е м а. Ранг матрицы не меняется при допустимых преобразованиях. Доказательство[†]. Остановимся на допустимых преобразованиях, связанных со строками (перестановка столбцов рассматривается аналогично перестановке строк). Возьмём какой-нибудь минор преобразуемой матрицы. Если преобразование его не затронуло или в преобразовании участвовали только его строки, то этот минор остаётся таким же, как был, либо равным нулю, либо отличным от нуля. Измениться, в этом смысле, минор может, только если в преобразовании участвовала строка, назовём её действующей, элементы которой в минор не входили. При этом возможны два случая: а) изменяемая строка, была переставлена с действующей; б) к изменяемой строке прибавлена действующая строка, умноженная на число, не равное нулю. Пусть ранг матрицы равен r. Это значит, что она содержит минор r -го порядка, отличный от нуля. Предположим, что этот минор в результате допустимого преобразования стал равным нулю, такое возможно. В случае а) в преобразованной матрице возьмём минор, составленный из строк выделенного нами минора, не затронутых преобразованием, и строки, оказавшейся на месте действующей. Этот минор может отличаться от исходного минора лишь знаком и, следовательно, не равен нулю. В случае б) преобразованный минор, с одной стороны, равен нулю, с другой (в силу шестого свойства) – сумме исходного (не равного нулю) минора и другого минора, отличающегося от первого тем, что элементы изменяемой строки заменены элементами действующей строки, умноженной на число, отличное от нуля. Это значит, что минор преобразованной матрицы, составленный из строк исходного минора, не затронутых преобразованием, и действующей строки, отличен от нуля. И в том, и в другом случае преобразованная матрица обладает минором r -го порядка, отличным от нуля, так что ранг матрицы не уменьшился. Теперь покажем, что все миноры (r +1)-го порядка преобразованной матрицы (так же как и исходной) равны нулю. Предположим, что какой-нибудь минор (r +1)-го порядка исходной матрицы перестал быть равным нулю. В случае а) это означает, что он содержит элементы r строк, не участвующих в перестановке, и часть элементов действующей строки. Но минор с такими строками уже был в исходной матрице и должен был быть равным нулю как минор (r +1)-го порядка, поэтому наше предположение о том, что рассматриваемый минор стал отличным от нуля ошибочно. В случае б) преобразованный минор представляет собой сумму исходного минора и другого минора исходной матрицы, умноженного на число. Оба минора, будучи минорами (r +1)-го порядка, равны нулю, значит, равна нулю и их сумма. Значит, и в этом случае следует признать ошибочность нашего предположения. Таким образом, ранг матрицы не увеличился. Итак, если матрица A при помощи допустимых преобразований, приведена к матрице Вот почему к треугольному виду можно привести только невырожденную матрицу. Пример. Чтобы вычислить ранг матрицы
При помощи понятия «ранг матрицы» можно гораздо короче сформулировать полученные нами ранее условия совместности и несовместности систем линейных уравнений. Рассматривая преобразованную расширенную матрицу Несовместность системы, как мы видели, была связана с тем, что столбец Поскольку матрица Т е о р е м а (Кронекера-Капелли). Для того чтобы система линейных уравнений была совместна, необходимо и достаточно, чтобы ранг матрицы коэффициентов при неизвестных был равен рангу расширенной матрицы. С использованием понятия ранга матрицы легко также переформулировать условия, при которых однородные системы линейных уравнений имеют либо одно, либо бесконечно много решений. Если ранг матрицы коэффициентов однородной системы линейных уравнений равен числу неизвестных, то система имеет единственное (нулевое) решение, если же ранг этой матрицы меньше числа неизвестных, система имеет бесконечное множество решений (в том числе ненулевые). Из этого следует, что, для того чтобы однородная система линейных уравнений с квадратной матрицей коэффициентов имела ненулевые решения, необходимо и достаточно, чтобы главный определитель этой системы был равным нулю (необходимость этого условия уже была установлена). собственные числа и собственные векторы О п р е д е л е н и е. Ненулевой алгебраический вектор X и число λ называются, соответственно, собственным вектором и собственным числом квадратной матрицы A, если каждому собственному числу λ отвечает бесконечно много собственных векторов, поскольку при умножении собственного вектора на какое-нибудь отличное от нуля число t, получается также собственный вектор, Матричное равенство Для того чтобы эта система имела ненулевое решение, необходимо и достаточно, чтобы её главный определитель Уравнение Приведём пример вычисления собственных чисел и собственных векторов квадратной матрицы. Пусть Подставляя последовательно эти числа в систему Если
Пусть Если
Пусть Если
|
|||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 1243; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.013 с.) |

 .
. матрица
матрица  является расширенной матрицей.
является расширенной матрицей. ~
~  ~
~  ~
~  .
. ~
~ 
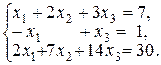
 ~
~  ~
~  ~
~ 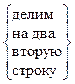 ~
~ ~
~ 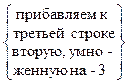 ~
~  ~
~ 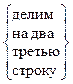 ~
~ 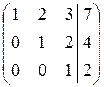 .
. . Подставив во второе уравнение
. Подставив во второе уравнение  , найдём, что
, найдём, что 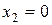 . Затем, подставляя в первое уравнение
. Затем, подставляя в первое уравнение  . Решение системы методом Гаусса завершено.
. Решение системы методом Гаусса завершено. ~
~  ~
~  , откуда
, откуда  .
. E
E
 .
.
.
.
.
.
 0
0

 k n-k
k n-k . Столбец B также изменится и станет столбцом
. Столбец B также изменится и станет столбцом  . В результате получается преобразованная расширенная матрица
. В результате получается преобразованная расширенная матрица  .
. , и хотя бы один элемент столбца
, и хотя бы один элемент столбца  (
( ), то система несовместна, так как содержит уравнение
), то система несовместна, так как содержит уравнение  , не имеющее решений при
, не имеющее решений при  .
.
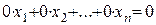 и им удовлетворяют любые числа.Поэтому можно считать, что
и им удовлетворяют любые числа.Поэтому можно считать, что  .
. и
и  . При
. При
 E
E
 , так же как и
, так же как и  . Система, очевидно, совместна. Найдём все её решения. Отбрасывая третью и четвёртую строчки (они состоят из нулей), получим систему
. Система, очевидно, совместна. Найдём все её решения. Отбрасывая третью и четвёртую строчки (они состоят из нулей), получим систему  . Пусть t, u, v – произвольные числа. Положим свободные неизвестные равными этим числам, то есть будем считать, что
. Пусть t, u, v – произвольные числа. Положим свободные неизвестные равными этим числам, то есть будем считать, что 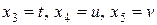 . Тогда из первого уравнения следует, что
. Тогда из первого уравнения следует, что  , а из второго, что
, а из второго, что  . Полученные формулы вычисления неизвестных дают бесконечно много решений.
. Полученные формулы вычисления неизвестных дают бесконечно много решений.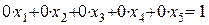 . Такое уравнение, а вместе с ним и система, решений не имеет.
. Такое уравнение, а вместе с ним и система, решений не имеет.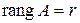 ), если какой-нибудь её минор r -го порядка отличен от нуля, а все миноры (r +1)-го порядка (если они существуют) равны нулю.
), если какой-нибудь её минор r -го порядка отличен от нуля, а все миноры (r +1)-го порядка (если они существуют) равны нулю. не превышает наименьшего из чисел m и n, так как минор не может содержать строк и столбцов больше, чем сама матрица. Если
не превышает наименьшего из чисел m и n, так как минор не может содержать строк и столбцов больше, чем сама матрица. Если  и найдётся минор порядка m, отличный от нуля, то ранг матрицы равен m. Если
и найдётся минор порядка m, отличный от нуля, то ранг матрицы равен m. Если  и найдётся минор порядка n, отличный от нуля, ранг матрицы равен n.
и найдётся минор порядка n, отличный от нуля, ранг матрицы равен n. ,
,  ,
,  .
. E
E
 ……..
……..
……..
……..
……..
……..

 0
0

 k n-k
k n-k , нужно привести её к каноническому или почти каноническому виду. Это было сделано нами на страницах 16 и 17. Были полученные две матрицы:
, нужно привести её к каноническому или почти каноническому виду. Это было сделано нами на страницах 16 и 17. Были полученные две матрицы:  (канонического вида) и
(канонического вида) и 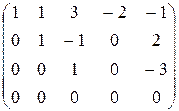 (почти канонического вида). В левом верхнем углу каждой из этих матриц расположена невырожденная квадратная матрица третьего порядка. Все миноры четвёртого порядка равны нулю, так как содержат строку, состоящую из нулей. Значит, ранг всех трёх матриц равен трём.
(почти канонического вида). В левом верхнем углу каждой из этих матриц расположена невырожденная квадратная матрица третьего порядка. Все миноры четвёртого порядка равны нулю, так как содержат строку, состоящую из нулей. Значит, ранг всех трёх матриц равен трём. , мы пришли к выводу, что всегда, когда система совместна, матрицы
, мы пришли к выводу, что всегда, когда система совместна, матрицы  имеют канонический вид с одним и тем же единичным (треугольным) блоком порядка k. Поэтому ранги обеих матриц равны k. Так что верно следующее утверждение: если система совместна, то
имеют канонический вид с одним и тем же единичным (треугольным) блоком порядка k. Поэтому ранги обеих матриц равны k. Так что верно следующее утверждение: если система совместна, то  .
. ). С помощью этого элемента можно составить отличный от нуля минор (k +1)-го порядка, присоединив к единичному (треугольному) блоку столбец
). С помощью этого элемента можно составить отличный от нуля минор (k +1)-го порядка, присоединив к единичному (треугольному) блоку столбец 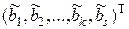 и строку
и строку  . Их общий элемент
. Их общий элемент  станет при этом (k +1)-м диагональным элементом минора. Ясно, что
станет при этом (k +1)-м диагональным элементом минора. Ясно, что 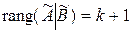 , тогда как
, тогда как  , то есть
, то есть 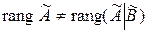 .
. получена из матрицы
получена из матрицы  при помощи допустимых преобразований, сохраняющих ранг матриц и не нарушающих равносильности соответствующих им систем, условия совместности и несовместности преобразованной системы, рассмотренные нами, можно отнести к исходной системе линейных уравнений. Таким образом, справедливо следующее утверждение.
при помощи допустимых преобразований, сохраняющих ранг матриц и не нарушающих равносильности соответствующих им систем, условия совместности и несовместности преобразованной системы, рассмотренные нами, можно отнести к исходной системе линейных уравнений. Таким образом, справедливо следующее утверждение. .
. . Обычно бывает достаточно найти один из них.
. Обычно бывает достаточно найти один из них.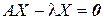 или, что то же самое,
или, что то же самое,  . Вынося за скобки X, получим равенство
. Вынося за скобки X, получим равенство  , которое можно рассматривать как матричную запись однородной системы линейных уравнений.
, которое можно рассматривать как матричную запись однородной системы линейных уравнений.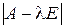 был равен нулю. Значит, число λ будет собственнымчислом матрицы A в том и только в том случае, когда
был равен нулю. Значит, число λ будет собственнымчислом матрицы A в том и только в том случае, когда  , то есть λ должно быть корнем этого уравнения.
, то есть λ должно быть корнем этого уравнения. , тогда
, тогда  – характеристическое уравнение этой матрицы. Вычислив определитель, получим уравнение
– характеристическое уравнение этой матрицы. Вычислив определитель, получим уравнение  , решив которое, найдём, собственные числа
, решив которое, найдём, собственные числа  ,
,  ,
,  .
. ,
,  ,
,  .
. , то
, то 
 и
и  . Решаем систему методом Гаусса.
. Решаем систему методом Гаусса. ~
~  ~
~  ~
~  .
. [‡], тогда
[‡], тогда 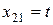 ,
,  , так что
, так что  .
.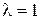 , то
, то  и
и  .
. ~
~  ~
~  ~
~  .
. **, тогда
**, тогда  ,
,  , так что
, так что 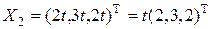 .
. , то
, то  и
и 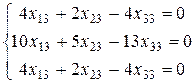 .
.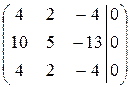 ~
~  ~
~ 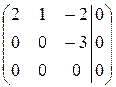 ~
~  . Вторая строка соответствует равенству
. Вторая строка соответствует равенству  , то есть
, то есть  нельзя выбирать произвольно. Пусть
нельзя выбирать произвольно. Пусть  , тогда
, тогда  , так что
, так что  .
.


